Дифференцируемое многообразие

Определение метрического пространства. Примеры.

Абстрактное понятие метрики является обобщением понятия «расстояние». При этом свойства расстояния (не отрицательность, равенство нулю т.и.т.т.к. точки пространства совпадают; симметричность; неравенство треугольника) положено в основу метрики.

Опр1: Метрикой на множестве Х называется fия ρ: Х×Х → R, удовлетворяющая следующим аксиомам:

1) ρ(x,y)≥0, причём ρ(x,y)=0 ⇔x=y;

2) ρ(x,y)=ρ(y,x);

3) ρ(x,y)≤ρ(x,z)+ ρ(z,y)∀x,y,z∈ Х;

!Перечисленные аксиомы не являются независимыми.

Примеры метрических пространств:

1(рисунок №1 метрического пространства R²=RxR)

ρ(М₁,М₂)=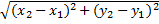

2) Rⁿ: x=(x1,x2,…,xn), y=(y1,y2,…,yn)

ρ(x,y)= 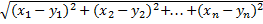Евклидова метрика

3) С[a,b]-пространство непрерывных fий на отрезке [a,b];

(рисунок №2 непрерывные фии на а,б)

f(x) и g(x) непрерывны на [a,b].

ρ(f,g)=max|f(x)-g(x)|

Открытые и замкнутые мн-ва в метрическом пространстве.

R(X,p)
Опр.1: Мн-во Y⊂Xназывается открытым в простр-ве R=(X,p), если вместе с каждой своей точкой xϵYоно содержит некоторый шар B(x,r) ⊂Y.
B(x,r)=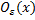
Y–открыто, если для любого xϵYсущ-ет 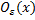ϵY.

Опр.2: Мн-во B⊂X называется замкнутым, если его дополнение X-Bявляется открытым мн-вом.

(рисунок №7 область Aи в ней точка Х внутри)

Aϵ 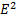- открытое мн-водля любого xϵAсущ-ет 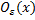⊂A

(рисунок №8 область А и точка Х вне)

B⊂ 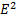- замкнутое мн-во 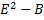- открытоедля любого xϵ 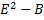сущ-ет ⊂

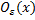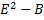
Свойства открытых и замкнутых множеств.

Пусть R=(x,ρ)-метрическое пространство

1) { } –открытое множество в R

2) { } –замкнутое множество в R

Тогда:

1) 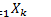- открытое множество

(Объединение любого числа открытых множеств открыто.)

2) 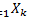- открытое множество

(Пересечение конечного числа открытых множеств открыто.)

3) 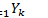- замкнутое множество

(Объединение любого числа закрытых множеств закрыто.)

4) 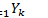- замкнутое множество

(Пересечение конечного числа закрытых множеств закрыто.)

5) 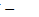открытое, Y - замкнутое

Доказательство:

1) – открытое множество

– открытое множество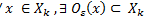

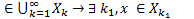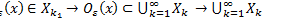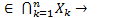
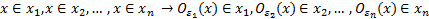
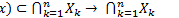(открытое множество)

3) 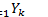(замкнутое множество)

4) 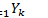(замкнутое множество)

5) ,

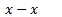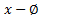
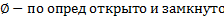
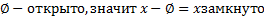
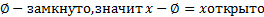
Сходящиеся последовательности в метрическом пространстве. Их свойства

Опр1. Последовательность ξ = {х1, Х2,..., х_n,...} точек метрического пространства (M,p) называется сходящейся к точке a ϵM, точка a называется пределом этой последовательности, если ,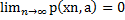
это равносильно тому, что для любого вещественного числа ξ>0 {\displaystyle \epsilon >0} существует натуральное число n₀{\displaystyle n_{0}}nnnnnтакое, что для любого номера {\displaystyle ~n>n_{0}}n>n₀выполняется неравенство {\displaystyle ~\rho (x_{n},a)<\epsilon } p(x_n ,a)< ξ

Св-во 1. (Единственность предела). Если у последовательности {x_n} существует предел, то он единственный.

Доказательство. Допустим, что у данной последовательности существует несколько пределов и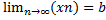

Тогда, по определению предела последовательности: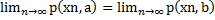

Согласно неравенству треугольника и свойству неотрицательности метрики 0≤p(a,b)≤p(a,x_n)+p(x_n ,b) .

Переходя к пределу при 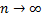получим: 0 ≤ p(a,b) ≤ 0 + 0=0

А из равенства нулю метрики для двух элементов следует их равенство.

Св-во 2. Если последовательность сходится, то она ограничена

Доказательство. Для того, чтобы доказать, что сх-ся пос-ть {x_n} элементов множества M ограничена, покажем, что все её члены содержатся в некотором шаре B конечного радиуса. Пусть последовательность {x_n} сходится в пространстве M, тогда последовательность {ρ (x_n, a)} сходится на множестве действительных чисел:

(ƎM>0), (nϵN) , p(x_n,a)≤M. Следовательно nϵN , x_nϵB[a,M]

Св-во 3. Если последовательность {xn} сходится к элементу a, то и любая её подпоследовательность сходится к тому же самому элементу.

Св-во 4 (Непрерывность метрики).: Пусть заданы две последовательности

{x_n},{y_n}, причем , ,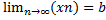тогда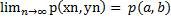

Доказательство. Согласно неравенству четырёхугольника, для каждого номера n : |p(x_n,y_n)-p(a,b)|≤ p(x_n,a)-p(y_n,b).

Переходя к пределу в правой и левой частях неравенства, и учитывая свойство неотрицательности метрики, получаем:

0≤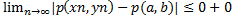

Отсюда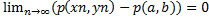

Предел разности равен разности пределов, поэтому

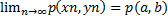Топологическое пространство

Метрическое пространство Х

p (x,y) – числовая ф-я p(x,y) ≥ 0

A1. p(x,y) = 0 <=> x=y

A2. 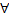x,y p(x,y) = p(y,x)

A3. 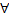x,y,z p(x,y) ≤ p(x,z)+p(z,y)

Теорема.

R=(x,p) - метрическое пр-ство

{X_k} – откр. мн-во в R,

{Y_k} – замкн. мн-во в R

X – произвольное мн-во

Говорят, что т. Х огран. точками τ, если на X опр. открыт. мн – во; τ = {Пустое множество,G_α}

Аксиомы тополог. пространства

А1. 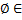τ ( 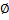– откр.)

А2. 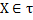(Х - откр.)

А3. 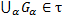( 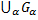- откр.)

А4. 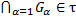( 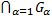- откр.)

Пример.

(х, τ) – топологич. пространство; Х – произв. мн-во; – открыт. мн-во

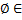А1. τ₁

А2.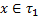

А3.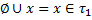

А4. . .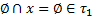

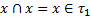
Аксиомы отделимости

Пусть X — множество и τ— система его подмножеств, удовлетворяющая двум условиям:

а) пересечение всякой конечной подсистемы элементов τ ∈ τ;

б) ∪ всякой подсистемы элементов τ ∈ τ.

Из а) вытекает, что X принадлежит τ, поскольку X — пересечение пустой подсистемы системы τ. Аналогично из б) вытекает, что (пустое множество) ∈ τ.

Пара (X, τ) называется топологическим пространством, а семейство τ— топологией.

Аксиомы отделимости:

1) Топологическое пространство X является Т₀пространством, if для ∀ х,у∈X по крайней мере одна из них имеет окрестность, не содержащую другую точку.

2) Пространство X называется Т₁-пространством, if для ∀ х,у∈X ∃ окрестность Ох, не содержащая точки у, и окрестность Оу, не содержащая точки х. Очевидно, X есть Т₁пространство т.и.т.т.к. все одноточечные подмножества X замкнуты.

3) Пространство X называется хаусдорфовым или Т₂-пространством, if для ∀ из X существуют непересекающиеся их окрестности.

4) Пространство X называется Т₃-пространством, if для ∀ х ∈ X и всякого не содержащего ее замкнутого множества F ∃ Ох ∩(зачёркнутое) OF.

5) Аксиомы Т₀,Т₁,Т₂идут в порядке усиления и дают все более узкие классы пространств. Так, пространство на

двухточечном множестве {а, Ъ}, открытыми в котором являются множества 0, {а}, {а, Ъ} (так называемое «связное двоеточие»), естьТ₀-пространство, но не Т₁-пространство.

6) Пространство, одновременно удовлетворяющее аксиомам Т₀ и Т₃, называется регулярным. Всякое регулярное пространство X хаусдорфово.

7) Пространство X называется Т₄-пространством, if любую дизъюнктную пару замкнутых в X множеств можно заключить в непересекающиеся окрестности.

Дифференцируемое многообразие

Опр 1. Многообразие М называется дифференцируемым многообразием если выполняется 2 условия:

1)Дана совокупность {U_i,Ф_j}_iϵj ,где {U_i}_iϵj –открытое покрытие М

U_i: Ф_i 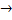V_iгомеоморфизм, которыйпереводит U_iв V_iϵ пл z.

2)При U_i⋂ U_i≠0 отображение

Ф_j Ф_i^-1=Ф_j (Ф_i^-1 (x₁,x₂) является С^-1 отображением

1. (рисунок №5: область с кружочками~на доске блинчики)

Покрытие М

МС ∪ U_i

{(U_i ,Ф_i )} Ф_i (U_i )=V_iϵ пл.z

2. (рисунок №6: деление клеток на 2ух столах)

U_i⋂ U_j ≠Ø

Ф_i (p)=(x₁,x₂) Ф_j (p)=(y₁,y₂) p= Ф_j (y₁,y₂)

15. Ориентируемые и неориентируемые поверхности. Лист Мебиуса, Бутылка Клейна.

Поверхность S наз-ся ориентированной, если на этой поверхности каждая замкнутая цепь когерентно-ориентирована.

Неориентированные пов-ти:

1) Лист Мебиуса

Одним из способов представления листа Мёбиуса как подмножество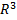

Является параметризация:

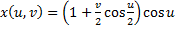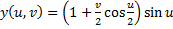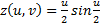где 0 ≤ u< 2π и -1 ≤ v ≤ 1. Эти формулы задают ленту Мёбиуса ширины 1, чья центральная окружность имеет радиус 1 , лежит в плоскости xy с центром в (0, 0, 0). Параметр u пробегает вдоль ленты, в то время как v задаёт расстояние от края.

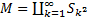(формула из лекций)

2) Бутылка Клейна

Параметризация:

Бутылка Клейна в виде восьмёрки имеет довольно простую параметризацию:

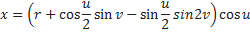
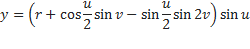
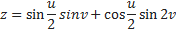
В этом виде самопересечение имеет форму геометрического круга в плоскости XY. Константа r равна радиусу круга. Параметр u задаёт угол на плоскости XY и vобозначает положение около 8-образного сечения.

Способы задания поверхности

1) Аналитический способ:

а) Явный вид: z=f(x,y), (x,y)∈D(рисунок №3 явный вид поверхности)

б)Неявный вид: F (x, y, z) = 0 или z = Ф(х, у); S: x²+y²+z²=R²; F(x,y,z)= x²+y²+z²-R²=0

2) Параметрический способ:

Поверхность задаётся системой уравнений, определяющих зависимость координат точек поверхности от некоторого параметра:

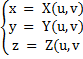(u,v)∈D

3) Векторный способ: (рисунок № 4 векторное задание поверхности)

R = R(u,v) = x(u,v)i + y(u,v)j + z(u,v)k

If один из параметров принять постоянным, например, задаться v=v₁, то вектор fии R=R(u,v₁) опишет на поверхности некоторую линию v₁=const, называемую координатной линией. Совокупность линий v_i=const (i=1, …, m) образует линейный каркас.

Дата добавления: 2018-02-28; просмотров: 352; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!