Предварительная обработка результатов измерений
Методика обработки результатов прямых однократных измерений
При однократном измерении погрешность его результата вычислить невозможно, т.к. неизвестно истинное значение измеряемой величины. Судить о точности результата можно только на основании нормируемых метрологических характеристик использованных средств измерений. Для измерительных приборов такой метрологической характеристикой может служить предел допускаемой основной погрешности, который может быть вычислен по классу точности этого прибора. Класс точности средств измерений обычно обозначается числом, представляющим собой приведенную допускаемую погрешность, выраженную в процентах. Однако в значительном числе случаев указанный способ не применим (например, для классификации концевых мер длины, гирь, ряда других мер, а также некоторых измерительных приборов).
При измерениях случайные и систематические погрешности проявляются одновременно. Если систематические погрешности отсутствуют или учтены поправками, то суммарная предельная погрешность измерения равна
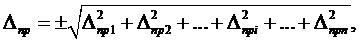
где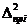 
- предельные погрешности измерительных приборов, установочных мер, температурных деформаций, деформаций от измерительного усилия, базирования приборов и других факторов, из которых складывается суммарная погрешность данного измерения.
При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений (повторных наблюдений) одной и той же постоянной, неизменяющейся величины мы получаем результаты наблюдений, некоторые из которых отличаются друг от друга, а некоторые совпадают. Такие расхождения в результатах измерений говорят о наличии в них случайных погрешностей. Поскольку производится измерение определенного параметра конкретного объекта, то существует некоторое истинное значение этого параметра, которое невозможно определить из-за погрешностей отдельных наблюдений.
|
|
|
Теория вероятностей дает математические методы изучения свойств случайных событий в больших совокупностях. Теория погрешностей, использующая математический аппарат теории вероятностей и математической статистики, основывается на рассмотрении появления случайных погрешностей при многократно повторяемых наблюдениях как случайных событий.
Методика обработки результатов прямых равноточных многократных
Измерений
Статистическая обработка экспериментальных выборок выполняется в такой последовательности:
· исключить (или уменьшить) систематические составляющие погрешности из результатов наблюдений одним из известных способов: введения поправок, замещения, компенсации, противопоставления;
|
|
|
· проверить соответствие экспериментального закона распределения теоретическому, нормальному (аналитическим или графоаналитическим способом). При сравнительно небольшом числе наблюдений такую проверку можно выполнить аналитическим способом – с помощью «критерия W». Расчет с помощью «критерия W» выполняется для выборок объемом от 3 до 50 результатов наблюдений. Для этого вычисляются характеристики
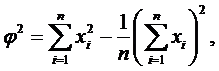
Отсюда критерий
W = (b/j)2.
Задавшись определенным уровнем значимости a,отображающимнаибольшую вероятность ошибочности гипотезы о принадлежности данной выборки к нормальной генеральной совокупности, находим значениеW* в справочниках. При W* > W*можно предполагать, что гипотеза справедлива и опытное распределение не противоречит нормальному закону распределения. При W* < W*опытное распределение не соответствует нормальному закону.
Для случая, когда можно предполагать, что данная выборка является частью генеральной совокупности, распределенной по нормальному закону, обработка продолжается;
· вычислить наиболее вероятное значение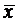 
искомой величины как среднее арифметическое выборки
|
|
|
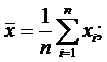
· вычислить среднеквадратичное отклонение s результата наблюдения по формуле
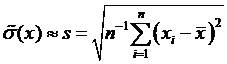
или формуле Бесселя
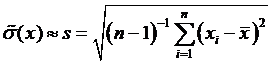
или формуле Петерса для упрощенного вычисления с.к.о.
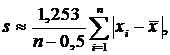
а для точных расчетов, учитывающих ограниченность числа опытов, по формуле
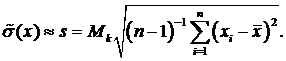
Значения коэффициента Mkприведены в справочниках, например / 4 /;
· при подозрении анормальности некоторого результата наблюдения xk, который заметно отличается от остальных в выборке, вычислить показатель анормальности для этого результата
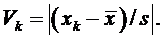
После этого сопоставить значение показателя Vk с табличной величиной βдля данного объема выборки и принятой вероятности γ. Если подозрения подтвердятся (критерием анормальности является условие Vk ³ β), этот результат наблюдения должен быть из выборки исключен, а значения 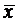и sвычислены заново (для этой же выборки, но без xk);
· вычислить коэффициент вариации v для данной выборки
v = 100 s/ , %;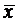
· вычислить среднеквадратичное отклонение результата измерения
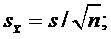
· вычислить доверительные границы εслучайной составляющей погрешности общего результата измерения
xн = 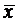- ε; xв = 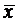+ ε,
где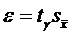 
,
tγ - коэффициент доверия, значения которого приведены в зависимости от числа степеней свободы k = n – 1 и γ,
|
|
|
γ - двусторонняя доверительная вероятность.
Обычно для технических расчетов вычисление доверительных границ производится с доверительной вероятностью равнойγ = 0,95, в отдельных случаях, когда эксперимент невозможно повторить, принимают γ = 0,99 и только в особо ответственных случаях, когда результаты эксперимента влияют на жизнь и здоровье людей, допускается принимать γ = 0,999;
· вычислить доверительные границы общей погрешности результата измерения. Если доверительные границы неисключенных остатков систематической составляющей погрешности результата измерения близка к нулю, можно принять
Δ A » ε;
· записать результат прямого измерения в виде
x = A ± Δ A; γ = 0,95,
где А – наиболее вероятное значение результата измерения (A » );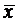
Δ A – доверительная граница погрешности измерения.
Полная форма записи обязательна в том случае, если γ¹0,95. При γ=0,95 значение вероятности в записи результата измерения часто опускают.
· Следует отметить, что существует следующие три основные правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:
· погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной - если первая есть 3 и более;
· результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности;
· округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.
Дата добавления: 2018-02-28; просмотров: 755; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!