Двойные интегралы методические указания и контрольные задания

Стр 1 из 2Следующая ⇒

1. Свойства двойных интегралов. Примеры решения задач. Пусть функция z=f (x,y)определена и непрерывна в ограниченной замкнутой области D плоскости O_xy. Разобьем область D произвольным образом на n областей S ₁, S ₂, …, S_n, в каждой из них произвольным образом выберем по точке: 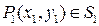, , 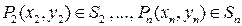которые назовём точками пунктуации. Обозначим через 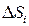- площадь, а через 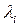- расстояние между двумя наиболее удаленными точками i -ой области (диаметр i- ойобласти), i= 1,…, n. Пусть .

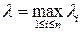ОПРЕДЕЛЕНИЕ. Интегральной суммой Римана функции z=f (x,y)по области D называется

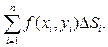(1)

Заметим, что сумма зависит от способа разбиения области D на части и от способа выбора точек пунктуации.

ОПРЕДЕЛЕНИЕ. Если существует предел интегральной суммы Римана (1) при , и этот предел не зависит ни от способа разбиения области, ни от выбора точек пунктуации, то он называется двойным интегралом от функции z=f (x,y)по области D и обозначается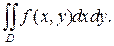

Таким образом, 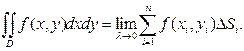(2)

Отметим, что согласно определению 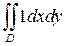равен площади области D. Свойства двойных интегралов аналогичны свойствам определенных интегралов. Выделим два из них, наиболее часто используемых на практике.

1) Свойство линейности. Если функции f (x,y)и g(x,y) интегрируемы в области D, то справедлива формула:

2) Свойство аддитивности. Если область D разбита на две области D ₁и D ₂ без общих точек, и функция f (x,y)интегрируема в области D, то справедлива формула:

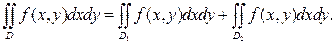
ТЕОРЕМА 1. Если область D ограничена слева и справа вертикальными прямыми x=a, x=b, а снизу и сверху – кривыми 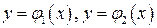,причем функции 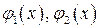- непрерывны и 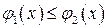на промежутке [ a,b ](Рис.1), то

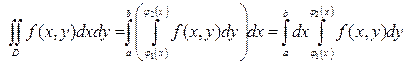. (3)

Таким образом, вычисление двойных интегралов сводится к последовательному вычислению двух интегралов, сначала вычисляется интеграл по переменной y (x - параметр), а потом полученный результат интегрируется по x, то есть двойной интеграл представим в виде повторных интегралов.

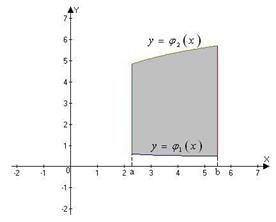Рис.1.

Область D, как в теореме 1, называется правильной в направлении оси Oy.

ПРИМЕР 1. Вычислить двойной интеграл: 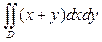по области D, ограниченной линиями: 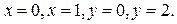РЕШЕНИЕ. Согласно теореме 1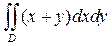 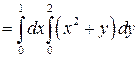. Сначала вычислим интеграл по переменной y (x – параметр): 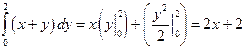. Окончательно имеем .

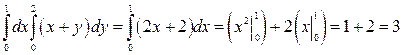ПРИМЕР 2. Вычислить двойной интеграл , где область D ограничена линиями: (рис. 2).

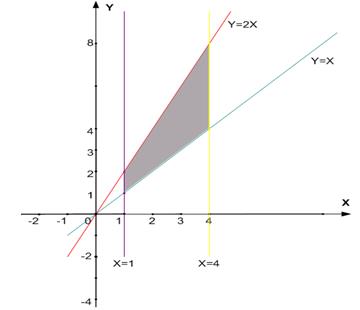Рис. 2.

Решение. В силу теоремы 1 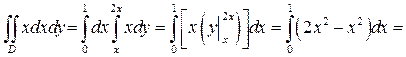= 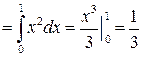. Заметим, что если кривая (или ) на промежутке [ a,b ]задается различными аналитическими выражениями, например, 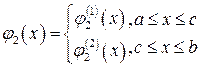, то интеграл справа в (3) записывается в виде суммы двух интегралов

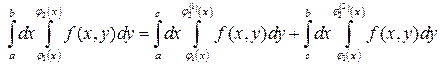. (4)

Пример 3. Вычислить двойной интеграл 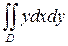, где область D ограничена линиями: 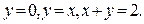ПЕРВЫЙ СПОСОБ РЕШЕНИЯ. Изобразим область D на плоскости (рис.3)

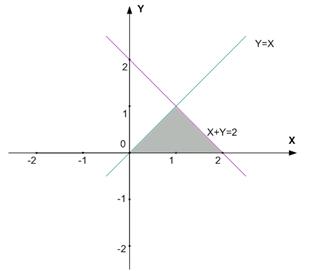Рис. 3.

Тогда 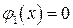и, если x меняется от 0 до 1, то 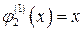, а если же если x меняется от 1 до 2, то 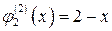и по формуле (4), имеем

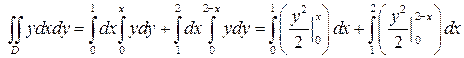
или

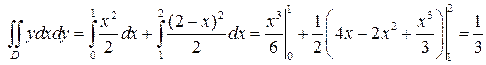Переменные x,y в двойном интеграле равноправны, то есть, если область D ограничена снизу и сверху горизонтальными прямыми y=c, y=d, а слева и справа - кривыми 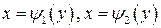, причем 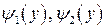непрерывны и 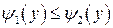на промежутке [ c,d ](Рис.4), то

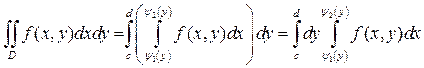(5)

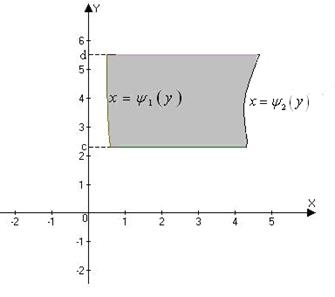Рис. 4.

Такая область называется правильной в направлении оси Ox.

ВТОРОЙ СПОСОБ. В этот раз воспользуемся формулой (5), тогда

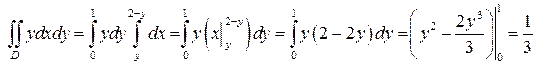Рассмотрим ещё один пример применения формул (3) и (5) в зависимости от вида области D.

Пример 4. Вычислить двойной интеграл 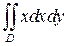, когда область интегрирования D ограничена линиями y= 2, y=x, y= 1 /x. Решение. Построим область интегрирования D (рис.5).

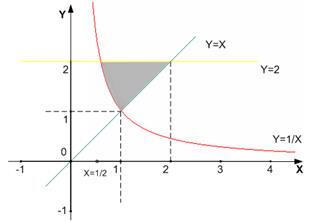Рис. 5.

ПЕРВЫЙ СПОСОБ. По формуле (4) получаем

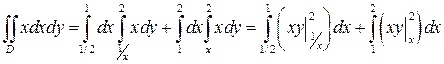или

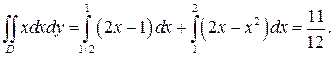
ВТОРОЙ СПОСОБ. Если же для вычисления данного интеграла применить формулу (5), то

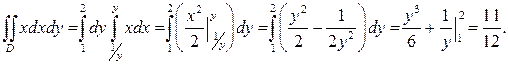
Теорема 2 (о замене переменных в двойном интеграле). Пусть выполняются условия:

1) функции x=x (u, v) и y=y (u, v)таковы, что каждой точке с координатами (x, y) из области D соответствует единственная точка с координатами (u, v) из области D ₁ и наоборот;

2) функции x=x (u, v) и y=y (u, v)имеют непрерывные частные производные по переменным u и v в области D ₁; 3) функция z=f (x, y) определена и интегрируема в области D.

Тогда справедлива формула: 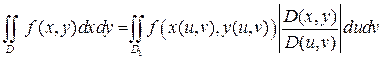, (6)

где 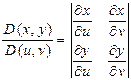- якобиан перехода от декартовых координат к криволинейным координатам. Частным случаем криволинейных координат для двойного интеграла являются полярные координаты: 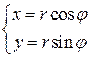, для которых якобиан равен 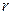и формула (6) примет вид:

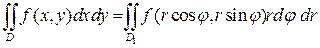(7)

ПРИМЕР 5. Перейдя к полярным координатам, вычислить интеграл: 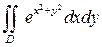по области D, заданной ограничениями 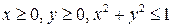. Решение. Положим 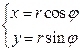и применим формулу (7). Так как 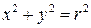, то 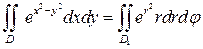. Областью интегрирования исходного интеграла является четверть круга радиуса R =1 с центром в начале координат (рис. 6). Следовательно, в области D ₁ переменная 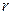изменяется от 0 до 1 и 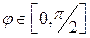. Таким образом, имеем:

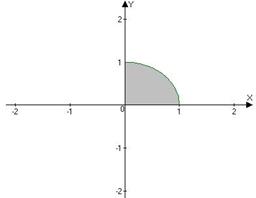Рис. 6.

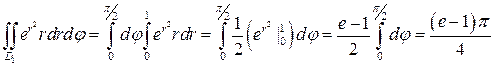Пример 6. Найти площадь фигуры, ограниченной линией, задаваемой уравнением: 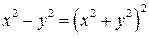. Решение. Площадь области S будет равна 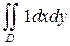, где область D ограничена линией: 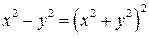. Отметим, что при замене переменной x (y) на – x (- y) уравнение линии не меняется, следовательно, область D будет симметричной относительно координатных осей.

Перейдем к полярным координатам: 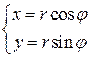. Подставив x,y в уравнение линии, получаем, что 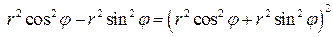или 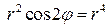. Таким образом, 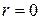и 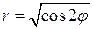, , 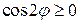тогда 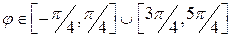. Искомая область D представлена на рисунке 7. 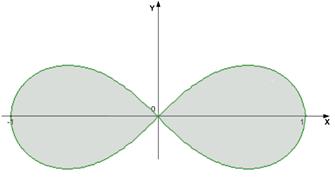Рис. 7.

Таким образом, .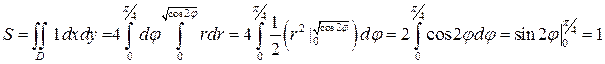

Дата добавления: 2015-12-20; просмотров: 11; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!