Основные выводы и результаты
· Сети Петри это инструмент для математического моделирования и исследования сложных систем. Они предназначены для моделирования систем, которые состоят из множества взаимодействующих друг с другом компонент.
· Используются два способа моделирования систем сетью Петри: строится система и моделируется сетью Петри; строится оптимальная модель системы в виде сети Петри, на основе которой разрабатывается система.
· Представление системы сетью Петри основано на понятиях событие и условие. Возникновением событий управляет состояние системы, которое может быть описано множеством условий.
· В сетях Петри отсутствует измерение времени. В них учитывается лишь важнейшее свойство времени – частичное упорядочение событий.
· Сети Петри удачно представляют структуру и управление программ. Они предназначены для моделирования упорядочения действий и потока информации, а не для вычисления значений.
· Cети Петри используют для моделирования параллельных систем взаимодействующих процессов. Они могут моделировать различные механизмы синхронизации процессов.
· Качество моделирования систем сетями Петри обусловлено возможностью исследования их поведения на основе анализа свойств моделирующей сети Петри.
· Существуют методы автоматического анализа свойств сетей Петри.
· Теорема. Дерево достижимости сети Петри конечно.
· На основе дерева достижимости осуществляется анализ свойств сетей Петри: анализ безопасности и ограниченности, сохранения, покрываемости, живости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, эквивалентности.
|
|
|
Контрольные вопросы и задания
1. Постройте граф сети Петри для следующей структуры сети Петри: P = { p1, p2, p3, p4 }, T = { t1, t2, t3, t4 }, I (t1) = {}, I (t2) = { p1 }, I (t3) = { p2, p4 }, I (t4) = {}, I (t5) = { p3 }, O (t1) = { p1 }, O (t2) = { p2 }, O (t3) = { p1, p3 }, O (t4) = { p3 }, O (t5) = { p4 }.
2. Изобразите граф сети Петри следующей структуры: P = { p1 p2 }, T = { t1, t2, t3 }, I (t1) = { p1 }, I (t2) = { p1 }, I (t3) = { p2 }, O (t1) = { p1, p2 }, O (t2) = { p2 }, O (t3) = {}.
3. Какое значение для сети Петри имеет маркировка?
4. Для структуры сети Петри: С = (P, T, I, O), P = { p1, p2, p3, p4, p5 }, T = { t1, t2, t3, t4 }, I (p1) = {}, I (p2) = { t1, t4 }, I (p3) = { t1, t4 }, I (p4) = { t3 }, I (p5) = { t1, t2 }, O (p1) = { t1 }, O (p2) = { t2 }, O (p3) = { t2, t3 }, O (p4) = { t4 }, O (p5) = { t2 }, I (t1) = { p1 }, I (t2) = { p2, p3, p5 }, I (t3) = { p3 }, I (t4) = { p4 }, O (t1) = { p2, p3, p5 }, O (t2) = { p5 }, O (t3) = { p4 }, O (t4) = { p2, p3 } изобразите граф сети Петри и укажите на графе маркировку m = <1, 0, 1, 1, 0, 0>.
5. Сеть Петри задания 3 имеет маркировку m = <1, 2, 0, 0, 1>. Какие переходы в ней разрешены?
6. Сеть Петри задания 3 имеет маркировку m = <1, 2, 0, 0, 1>. Какая маркировка получится при запуске перехода t1?
7. Охарактеризуйте класс сетей Петри, для которых последовательность маркировок не определяет единственную последовательность запусков.
|
|
|
8. Покажите, что "m 
Nn, 
R (C, m) = Nn.
9. Докажите, что если m’ R (C, m), то R (C, m’) 
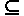R (C, m).
10. Докажите, что m’ R (C, m) тогда и только тогда, когда R (C, m’) 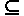R (C, m).
11. Разработайте теорию сетей Петри, разрешающую существование окрашенных фишек. Рассмотрите различия в определениях разрешенных переходов и запусков переходов.
12. Промоделируйте вычислительную систему с тремя процессами и четырьмя ресурсами: стример (устройство ввода с магнитной ленты), печатающее устройство, диск и два раздела памяти. Любой процесс может попасть в любой раздел. Использование ресурсов тремя процессами состоит в следующем:
а) процесс 1 запрашивает стример и печатающее устройство, а затем освобождает оба эти ресурса;
б) процесс 2 запрашивает стример и диск, а затем освобождает стример, запрашивает печатающее устройство и в конце концов, освобождает и печатающее устройство, и диск;
в) процесс 3 требует все три ресурса одновременно, и затем их освобождает.
13. Напишите программу, осуществляющую построение дерева достижимости по описанию сети Петри и начальной маркировке.
14. Постройте деревья достижимости для маркированной сети Петри, представленной заданием 4.
|
|
|
15. Какова цель анализа сети Петри? Какие вопросы о сети Петри можно задать?
| ЛИТЕРАТУРА Основная литература 1. Ершов А.П. Введение в теоретическое программирование. – М.: Наука, 1977. – 288 с. 2. Котов В. Е., Сабельфельд В.Н. Теория схем программ. - М.: Наука, 1991. – 248 с. 3. Андерсон Р. Доказательство правильности программ. - М.: Мир, 1982. – 168 с. 4. Себеста Р. Основные концепции языков программирования. – М.: Изд. дом «Вильямс», 2001. – 672 с. 5. Хоар Ч. Взаимодействующие последовательные процессы. - М.: Мир, 1989. – 264 с. 6. Котов В. Е. Сети Петри. - М.: Наука, 1984. – 160 с. 7. Питерсон Дж. Теория сетей Петри и моделирование систем. – М.: Мир, 1984. – 264 с. Рекомендуемая литература 8. Грис Д. Наука программирования. - М.: Мир, 1984. - 416 с. 9. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов – М.: Мир, 1979. – 536 с. 10. Барон Д. Рекурсивные методы в программировании. – М.: Мир, 1974. – 80 с. 11. Дал У., Дейкстра Э., Хоор К. Структурное программирование. – М.: Мир, 1975. – 248 с. 12. Непомнящий В.А., Рякин О.М. Прикладные методы верификации программ. Под ред. А.П.Ершова. - М.: Радио и связь, 1988. - 256 с. 13. Кнут Д. Искусство программирования для ЭВМ. Т.1, 2, 3. – М.: Мир, 1976 (1978). 14. Дейтл Г. Введение в операционные системы. Т.1. - М.: Мир, 1987. - 360 с. 15. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. 2 изд., - М.: Энергоиздат, 1988. - 480 с. 16. Шоломов Л.А. Основы теории дискретных логических и вычислительных устройств. - М: Наука, 1989. - 400 с. 17. Харари Ф. Теория графов – М: Мир, 1973. – 300 с. |
|
|
|
Дата добавления: 2015-12-20; просмотров: 25; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!