Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
AC = xb - xa;
BC = yb - ya.
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
AB = √AC2 + BC2.
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Пусть на плоскости введена прямоугольная декартова система координат Oxy и заданы координаты двух несовпадающих точек  и
и  . Нам требуется найти координаты
. Нам требуется найти координаты  и
и  точки С, которая делит отрезок АВ в отношении
точки С, которая делит отрезок АВ в отношении  , где
, где  - некоторое положительное действительное число.
- некоторое положительное действительное число.
Поясним смысл фразы: «точка С делит отрезок АВ в отношении  ». Это выражение означает, что точка С лежит на отрезке АВ (является внутренней точкой отрезка АВ) и отношение длин отрезков АС и СВ равно
». Это выражение означает, что точка С лежит на отрезке АВ (является внутренней точкой отрезка АВ) и отношение длин отрезков АС и СВ равно  (то есть, выполняется равенство
(то есть, выполняется равенство  ). Обратите внимание, что в этом случае точка А является как бы началом отрезка, а точка В – его концом. Если же сказано, что точка С делит отрезок ВА (а не АВ) в отношении
). Обратите внимание, что в этом случае точка А является как бы началом отрезка, а точка В – его концом. Если же сказано, что точка С делит отрезок ВА (а не АВ) в отношении  , то будет выполняться равенство
, то будет выполняться равенство 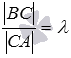 . Очевидно, что при
. Очевидно, что при  точка С является серединой отрезка АВ.
точка С является серединой отрезка АВ.
Поставленная задача может быть решена с помощью векторов.
Изобразим в прямоугольной декартовой системе координат некоторый отрезок АВ, точку С на нем и построим радиус-векторы точек А, В и С, а также векторы  и
и  . Будем считать, что точка С делит отрезок АВ в отношении
. Будем считать, что точка С делит отрезок АВ в отношении  .
.
|
|
|

Мы знаем, что координаты радиус-вектора точки равны соответствующим координатам этой точки, поэтому,  и
и  . Найдем координаты вектора
. Найдем координаты вектора  , которые будут равны искомым координатам точки С, делящей отрезок АВ в заданном отношении
, которые будут равны искомым координатам точки С, делящей отрезок АВ в заданном отношении  .
.
В силу операции сложения векторов можно записать равенства  и
и  . Их мы используем в следующем абзаце.
. Их мы используем в следующем абзаце.
Так как точка С делит отрезок АВ в соотношении  , то
, то  , откуда
, откуда  . Векторы
. Векторы  и
и  лежат на одной прямой и имеют одинаковое направление, а выше мы отметили, что
лежат на одной прямой и имеют одинаковое направление, а выше мы отметили, что  , поэтому, по определению операции умножения вектора на число справедливо равенство
, поэтому, по определению операции умножения вектора на число справедливо равенство  . Подставив в него
. Подставив в него 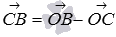 , имеем
, имеем  . Тогда равенство
. Тогда равенство  можно переписать как
можно переписать как 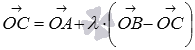 , откуда в силу свойств операций над векторами получаем
, откуда в силу свойств операций над векторами получаем  .
.
Осталось вычислить координаты вектора  , выполнив необходимые операции над векторами
, выполнив необходимые операции над векторами  и
и 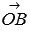 в координатах. Так как
в координатах. Так как  и
и  , то
, то  , следовательно,
, следовательно,  .
.
Таким образом, на плоскости координаты точки С, которая делит отрезок АВ в отношении  , находятся по формулам
, находятся по формулам  и
и  .
.
При рассмотрении линий используется термин текущая точка линии – переменная точка М(х,у), перемещающаяся вдоль этой линии. Координаты х и у текущей точки называются текущими координатами точки линии.
|
|
|
Если из уравнения (2.1) можно явным образом выразить у
через х, т. е. записать уравнение (2.1) в виде  , то кривую, определяемую таким уравнением, называют графиком функции f(х).
, то кривую, определяемую таким уравнением, называют графиком функции f(х).
Примеры.
1. Дано уравнение:  , или
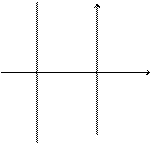
, или  . Если х принимает произвольные значения, то у принимает значения, равные х. Следовательно, линия, определяемая этим уравнением, состоит из точек, равноотстоящих от координатных осей Ох и Оу – это биссектриса I–III координатных углов (прямая
. Если х принимает произвольные значения, то у принимает значения, равные х. Следовательно, линия, определяемая этим уравнением, состоит из точек, равноотстоящих от координатных осей Ох и Оу – это биссектриса I–III координатных углов (прямая  на рис. 2.1).
на рис. 2.1).
Уравнение  , или
, или 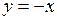 , определяет биссектрису II–IV координатных углов (прямая
, определяет биссектрису II–IV координатных углов (прямая  на рис. 2.1).
на рис. 2.1).


 у
у  у
у  у
у
С 
0 х 0 х С 0 х
рис. 2.1 рис. 2.2 рис. 2.3
2. Дано уравнение:  , где С – некоторая постоянная. Это уравнение можно записать иначе:
, где С – некоторая постоянная. Это уравнение можно записать иначе:  . Этому уравнению удовлетворяют те и только те точки, ординаты у которых равны С при любом значении абсциссы х. Эти точки лежат на прямой, параллельной оси Ох (рис. 2.2). Аналогично, уравнение
. Этому уравнению удовлетворяют те и только те точки, ординаты у которых равны С при любом значении абсциссы х. Эти точки лежат на прямой, параллельной оси Ох (рис. 2.2). Аналогично, уравнение  определяет прямую, параллельную оси Оу (рис. 2.3).
определяет прямую, параллельную оси Оу (рис. 2.3).
Не всякое уравнение вида F(x,y)=0 определяет линию на плоскости: уравнению  удовлетворяет единственная точка – О(0,0), а уравнению
удовлетворяет единственная точка – О(0,0), а уравнению  не удовлетворяет ни одна точка на плоскости.
не удовлетворяет ни одна точка на плоскости.
В приведенных примерах мы по заданному уравнению строили определяемую этим уравнением линию. Рассмотрим обратную задачу: составить по заданной линии ее уравнение.
|
|
|
3. Составить уравнение окружности с центром в точке Р(a,b) и
радиусом R.
○ Окружность с центром в точке Р и радиусом R есть совокупность точек, отстоящих от точки Р на расстоянии R. Это значит, что для любой точки М, лежащей на окружности, МР= R, если же точка М не лежит на окружности, то МР ≠ R.
Возьмем на окружности произвольную (текущую) точку М(х,у).
Тогда расстояние от М до Р, или длина вектора
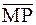 = –
= –  =(
=( ), равно R, т.е.
), равно R, т.е.
 . (2.2)
. (2.2)
Это и есть уравнение окружности, так как:
1) если точка М(х,у) принадлежит окружности, то ее координаты х и у удовлетворяют уравнению (2.2), поскольку  = R.
= R.
2) если точка N(x,y) не лежит на окружности, то ее координаты не удовлетворяют уравнению (2.2), поскольку в этом случае расстояние от N до Р не равно R.
Уравнение (2.2) можно упростить, возведя в квадрат правую и левую части:  .
.
Если центр Р окружности совпадает с началом координат, то  и уравнение принимает вид
и уравнение принимает вид 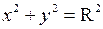 . ●
. ●
 рис. 69 рис. 69
| Если через некоторую точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве. Ох, Оу, Оz - оси абсцисс, ординат и аппликат. Координаты точки М записываются так: М (х; у; z). |
 рис. 70 рис. 70
| Зададим в пространстве прямоугольную систему координат Оxyz. На каждой из положительных полуосей отложим от начала координат единичные векторы (длины которых равны единице):
 .
Эти векторы назовем координатными векторами, они не компланарны. Поэтому любой вектор а можно разложить по координатным векторам, т.е. представить в виде: .
Эти векторы назовем координатными векторами, они не компланарны. Поэтому любой вектор а можно разложить по координатным векторам, т.е. представить в виде:
 причем коэффициенты разложения х, у, z определяются единственным образом.
причем коэффициенты разложения х, у, z определяются единственным образом.
|
Коэффициенты x, y и z в разложении называются координатами вектора  в данной системе координат.
в данной системе координат.
|
|
|
Координаты вектора  будем записывать в фигурных скобках после обозначения вектора:
будем записывать в фигурных скобках после обозначения вектора:  {x; y; z}.
{x; y; z}.
Координаты равных векторов равны.
Дата добавления: 2016-01-06; просмотров: 23; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
