Погрешности измерений. 3 страница
| (5.4) |
называемым дробью Стьюдента. Входящие в нее величины 
и 
вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений.
Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением:
| (5.5) |
где S(t, k) - плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна n - 1. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале 
, согласно выражению (5.5), вычисляется по формуле
или, поскольку S(t, k) является четной функцией аргумента t,
Подставив вместо дроби Стьюдента t ее выражение через 
и 
, получим окончательно
| (5.6) |
Величины 
, вычисленные по формулам (5.5) и (5.6), были табулированы Фишером для различных значений доверительной вероятности Р в пределах 0.10 - 0.99 при 
В табл.5.1 приведены значения для наиболее часто употребляемых доверительных вероятностей Р.
Таким образом, с помощью распределения Стьюдента по формуле (5.6) может быть найдена вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает 
, например 
и т.д. Итог измерений записывается в виде
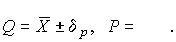
ПРИМЕР
При измерении ЭДС нормального элемента полечены следующие результаты:
| N опыта | ||||||
| ЭДС | 1,018456 | 1,018452 | 1,018453 | 1,018457 | 1,018455 | 1,018457 |
| N опыта | ||||||
| ЭДС | 1,018521 | 1,018456 | 1,018455 | 1,018454 | 1,018458 | 1,018457 |
Приняв доверительную вероятность р=0.99, определить результат, оценить случайную и относительную погрешности.
|
|
|
Для решения данной задачи предлагается следующая методика:
1. определяется неисправленный результат измерения
2. определяется относительная погрешность неисправленного результата измерений
3. вычисляем СКО погрешности неисправленного результата
3. исключаем явные промахи (аномальные результаты). Они не должны удовлетворять условию:
После исключения промахов (допустим, что их количество получилось r) определяем те же величины для исправленного результата измерений.
Математическое ожидание:
Относительная погрешность:
СКО результата:
Вычисляем результат измерений, как:
,
где tp - коэффициент Стьюдента.
Некоторые значения коэффициентов Стьюдента приведены в таблице:
Таблица 5.1
| Число измерений | Доверительная вероятность | ||
| 0.9 | 0.95 | 0.99 | |
| 6,31 | 12,72 | 63,7 | |
| 2,92 | 4,3 | 9,92 | |
| 2,35 | 3,18 | 5,84 | |
| 2,13 | 2,78 | 4,6 | |
| 2,02 | 2,57 | 4,03 | |
| 1,94 | 2,48 | 3,71 | |
| 1,9 | 2,37 | 3,5 | |
| 1,86 | 2,31 | 3,36 | |
| 1,83 | 2,26 | 3,25 | |
| 1,75 | 2,15 | 2,92 | |
| 1,72 | 2,08 | 2,84 | |
| 1,7 | 2,05 | 2,73 | |
| Более 30 | 1,65 | 1,96 | 2,58 |
По приведенной методике определяем математическое ожидание неисправленного результата:
|
|
|
m’=12.221531/12=1.0184609.
Определяем относительную погрешность неисправленного результата 
i’:
| 1’
| -4.8*10-6 | 5’
| -5,79*10-6 | 9’
| -5,79*10-6 |
| 2’
| -8.74*10-6 | 6’
| -3,83*10-6 | 10’
| -6,77*10-6 |
| 3’
| -7,76*10-6 | 7’
| 5,9*10-5 | 11’
| -2,85*10-6 |
| 4’
| -3,83*10-6 | 8’
| -4,8*10-6 | 12’
| -3,83*10-6 |
Определяем СКО неисправленного результата:
( ')=1,865*10-5.
Определяем границы, в которых находится результат измерения (выявляем явные промахи):
m’-m’*3 ( ')=1.0184039
m’+m’*3 ( ')=1.0185179.
По результатам измерений делаем вывод, что измерение № 7 является явным промахом и должно быть исключено из вычислений.
Определяем математическое ожидание исправленного результата:
m=1.0184553.
Определяем относительную погрешность исправленного результата di:
| 1
| 6.873*10-7 | 5
| -2.95*10-7 | 9
| -2.95*10-7 |
| 2
| -3.24*10-6 | 6
| 1.67*10-6 | 10
| -1.87*10-7 |
| 3
| -2.26*10-6 | 7
| -“- | 11
| 2.65*10-6 |
| 4
| 1.67*10-6 | 8
| 6.873*10-7 | 12
| 1.67*10-6 |
Определяем СКО исправленного результата:
( ')=1,837*10-6.
Определяем результат измерения:
Х=1.837±5.7*10-8, при доверительной вероятности р=0.99.
Моменты случайных погрешностей
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.
|
|
|
Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами.
Начальным моментом n-го порядка результатов наблюдений называется интеграл вида
| (6.1) |
представляющий собой математическое ожидание степени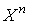 
.
При n=1
т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений.
Центральным моментом n-го порядка результатов наблюдений называется интеграл вида
| (6.2) |
Вычислим первый центральный момент:
| (6.3) |
Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю.
Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений.
|
|
|
| (6.4) |
При n=2
Дисперсия D[X] случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания.
Если математическое ожидание результатов наблюдений можно рассматривать в механической интерпретации как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести.
Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений:
| (6.5) |
С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины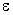 
, т. е. вероятность 
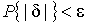. Для этого рассмотрим формулу, известную как неравенство Чебышева:
или 
Полагая 
, можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т. е. вероятность того, что случайная погрешность окажется больше 
:
Вероятность того, что погрешность измерения не превысит , составит соответственно
Неравенство Чебышева дает только нижнюю границу для вероятности 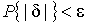, меньше которой она не может быть ни при каком распределении. Обычно 
значительно больше 0.89. Так, например, в случае нормального распределения погрешностей эта вероятность составляет 0.9973.
Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют наиболее важные черты распределения: положение центра распределения и степень его разбросанности. Для более подробного описания распределения используются моменты более высоких порядков.
Третий момент случайных погрешностей служит характеристикой асимметрии, или скошенности распределения. В общем случае любой нечетный момент случайной погрешности характеризует асимметрию распределения. Действительно, если распределение обладает свойством симметрии, то все функции вида 
, где s = l, 3, 5..., являются нечетными функциями 
(см. рисунок).
Поэтому все нечетные моменты, являющиеся интегралами этих функций в бесконечных пределах, должны равняться нулю. Отличие этих моментов от нуля как раз и указывает на асимметрию распределения. Простейшим из нечетных моментов является третий момент 
. Чтобы получить безразмерную характеристику, третий момент делят на третью степень среднеквадратического отклонения и получают коэффициент асимметрии, или просто асимметрию Sk распределения:
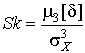
| (6.6) |
Рис. 6.1
Для иллюстрации сказанного на рис.6.1 приведены три кривые распределения случайных погрешностей с положительной, отрицательной и нулевой асимметрией.
Четвертый момент служит для характеристики плосковершинности или островершинности распределения случайных погрешностей. Эти свойства описываются с помощью эксцесса - безразмерной характеристики, определяемой выражением
| (6.7) |
Число 3 вычитают из отношения 
потому, что для широко распространенного нормального распределения погрешностей 
. Таким образом, для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные - положительным (см. рисунок 6.2).
Рис. 6.2.
АНАЛОГОВЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ.
АНАЛОГОВЫЕ ЭЛЕКТРОМЕХАНИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ.
Общие сведения.
Задачей электрических измерений является нахождение значений физических величин опытным путем с помощью специальных электрических средств и выражение этих значений в принятых единицах.
Средствами электрических измерений называют технические средства, используемые при электрических измерениях и имеющие нормированные метрологические характеристики.
Структурную схему аналогового электромеханического прибора в общем виде можно представить как:
Измерительная цепь – обеспечивает преобразование электрической величины Х в промежуточную электрическую величину Y, функционально связанную с величиной Х и пригодную для непосредственной обработки измерительным механизмом.
Измерительный механизм – основная часть прибора, предназначенная для преобразования электромагнитной энергии в механическую, необходимую для создания угла поворота a.
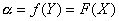
Отсчетное устройств о – состоит из указателя, связанного с измерительным механизмом и шкалы.
Указатели – бывают стрелочные (механические) и световые.
Шкала – совокупность отметок, представляющих ряд последовательных чисел вдоль какой либо линии.
По начертанию шкалы бывают прямолинейные (горизонтальные или вертикальные), дуговые (при дуге 
180°) и круговые (при дуге > 180°).
Цена деления шкалы определяются как:
где: Х – конечное значение шкала на данном пределе измерения,
N. число отметок шкалы.
Рассмотрим общий принцип действия измерительного механизма.
Обобщенная механическая схема измерительного механизма представлена на рисунке.
1 – ось, 2 – электромеханический преобразователь, приведенный к общему центру масс, 3 – стрелка, 4 – пружина, 5 – подшипниковые опоры.
Дифференциальное уравнение моментов, описывающее работу измерительного механизма, имеет вид:
где J – момент инерции подвижной части измерительного механизма,
- угол отклонения подвижной части,
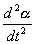- угловое ускорение.
На подвижную часть (при движении) воздействуют следующие составляющие моментов:
Вращающий момент – М- определяется скоростью изменения энергии электромагнитного поля 
, сосредоточенной в механизме, по углу отклонения .
Противодействующий момент - М - создается, как правило, при помощи спиральных пружин и растяжек
где: W – удельный противодействующий момент на единицу угла закручивания пружины (определяется её материалом, длиной и т.д.).
Момент успокоения – Мусп- момент сил сопротивления движению. Всегда направлен встречно вращающему моменту.
р- коэффициент успокоения (демпфирования) подвижной части.
После подстановки всех составляющих момента в основное уравнение получим:
или 
В статическом режиме, т.е когда стрелка прибора находится в неподвижном состоянии при каком то угле отклонения a, можно записать:
М=Мa.
По типу измерительного механизма приборы делятся на:
магнитоэлектрический механизм;
магнитоэлектрический механизм логометрического типа;
электромагнитный механизм;
электромагнитный механизм логометрического типа;
электромагнитный поляризованный механизм;
электродинамический механизм;
электродинамический механизм логометрического типа;
ферродинамический механизм;
ферродинамический механизм логометрического типа;
электростатический механизм:
измерительный механизм индукционного типа.
Общие технические требования ко всем электроизмерительным приборам нормируются ГОСТ 22261-82.
Условные обозначения определены в ГОСТ 23217-78.
ПРИБОРЫ МАГНИТОЭЛЕКТРИЧЕСКОГО ТИПА.
Общее устройство прибора электромагнитного типа показано на рисунке:
| a | б |
На рисунке (а) показана схема магнитоэлектрического механизма с подвижным магнитом, а на рисунке (б) - с неподвижным магнитом.
На рисунке приняты следующие обозначения:
стрелка; 2- катушка; 3- постоянный магнит; 4- пружина; 5- магнитный шунт; 6- полюсные наконечники.
Вывод уравнения шкалы прибора.
Уравнением шкалы называется математическая зависимость, дающая связь между измеряемой величиной и углом отклонения стрелки прибора.
Обозначим потокосцепление, связанное с катушкой как 
, тогда:
= I, где - энергия электромагнитного поля запасенной в измерительном механизме, I- величина тока, протекающего по катушке.
Если катушка имеет n витков, длина и ширина катушки соответственно l и b, магнитная индукция пронизываюшая катушку –В уравнение для потокосцепления в полном виде можно записать как:
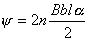или 
где S активная площадь катушки.
Подставив эти уравнения в уравнение для статики получим:
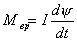
После подстановки имеем:
Тогда установившийся угол отклонения aу можно записать как:
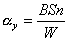или 
где Sп- чувствительность прибора.
Уравнение шкалы показывает, что шкала магнитоэлектрического измерительного механизма - линейна.
Следует отметить, что подвижная часть магнитоэлектрического механизма обладает относительно большим моментом инерции. Поэтому при включении в цепь переменного синусоидального тока, среднее значение которого за период равно нулю, средний вращающий момент также
равен нулю. Следовательно, данный механизм, примененный непосредственно может измерять только постоянные токи.
Магнитоэлектрический механизм логометрического типа.
Механизм устроен следующим образом: первая и вторая катушки формируют вращающие моменты М1 и М2 направленные всегда встречно друг другу.
Индексами 1- обозначены параметры, относящиеся к первой катушке, а индексами 2- ко второй.
Если моменты окажутся равными, тогда можно записать:
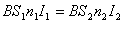
Откуда можно записать уравнение шкалы магнитоэлектрического логометра.
или 
Применяются логометрические механизмы, например в омметрах.
Необходимо отметить, что в некоторых типах логометров в отключенном состоянии стрелка может находиться в произвольном положении.
Достоинства магнитоэлектрических приборов:
Большой вращающий момент при малых токах, высокие классы точности, малое самопотребление.
Недостатки магнитоэлектрических приборов:
Сложность конструкции, высокая стоимость, невысокая перегрузочная способность,
Применение магнитоэлектрических измерительных механизмов.
Магнитоэлектрические гальванометры.
Гальванометрами называются приборы с высокой чувствительностью.
Устройство гальванометра показано на рисунке:
В общем, виде угол поворота подвижной части гальванометра можно записать как
Траектория движения подвижной части гальванометра во времени определяется показателем b, который называется степенью успокоения и определяется соотношением внутренних сопротивлений электрической части прибора и сопротивлением внешней цепи.
где: Rг- сопротивление рамки (катушки) гальванометра;
Rвн. кр- Критическое сопротивление внешней цепи;
Дата добавления: 2016-01-05; просмотров: 14; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!