Введение в математический анализ.
Приложение 1
Методические указания и задания на контрольные работы № 1 – 6
Задачи, включенные в контрольную работу, взяты из сборника задач, подготовленного коллективом преподавателей кафедры «Высшая и прикладная математика». Все задачи имеют тройную нумерацию, которая включает номер раздела из сборника задач, уровень сложности задачи и порядковый номер задачи. Студент выполняет те задачи, последняя цифра номера которых совпадает с последней цифрой его учебного шифра.
Перед выполнением контрольной работы студент должен ознакомиться с содержанием разделов рабочей программы, на освоение которых ориентирована выполняемая контрольная работа. Необходимую учебную литературу студент может найти в рабочей программе (в программе указана как основная, так и дополнительная литература).
Каждая контрольная работа выполняется в отдельной тетради, на обложке которой должны быть указаны: дисциплина, номер контрольной работы, шифр студента, курс, фамилия, имя и отчество студента. На обложке вверху справа указывается фамилия и инициалы преподавателя-рецензента. В конце работы студент ставит свою подпись и дату выполнения работы.
В каждой задаче надо полностью выписать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
Решение каждой задачи должно содержать подробные вычисления, пояснения, ответ, а также, в случае необходимости, и рисунки. После каждой задачи следует оставлять место для замечаний преподавателя-рецензента. В случае невыполнения этих требований преподаватель возвращает работу для доработки без ее проверки.
КОНТРОЛЬНАЯ РАБОТА № 1
Элементы векторной алгебры, аналитической геометрии и линейной алгебры
1.1.1. Найти косинус угла между векторами 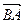 и
и 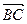 , если
, если 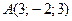 ;
; 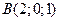 ;
; 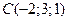 . Сделать чертеж.
. Сделать чертеж.
1.1.2. Найти косинус угла между векторами 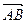 и
и 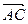 , если
, если 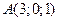 ;
; 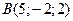 ;
; 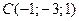 . Сделать чертеж.
. Сделать чертеж.
1.1.3. Найти угол между векторами 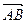 и
и 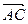 , если
, если 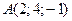 ;
; 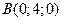 ;
; 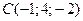 . Сделать чертеж.
. Сделать чертеж.
1.1.4. Найти угол между векторами 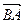 и
и 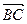 , если
, если 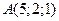 ;
; 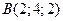 ;
; 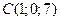 . Сделать чертеж.
. Сделать чертеж.
1.1.5. Найти угол между векторами 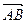 и
и 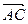 , если
, если 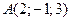 ;
; 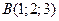 ;
; 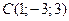 . Сделать чертеж.
. Сделать чертеж.
1.1.6. Найти угол между векторами 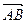 и
и 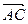 , если
, если 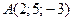 ;
; 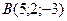 ;
; 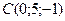 . Сделать чертеж.
. Сделать чертеж.
1.1.7. Найти косинус угла между 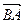 и
и 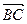 , если
, если 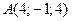 ;
; 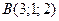 ;
; 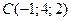 . Сделать чертеж.
. Сделать чертеж.
1.1.8. Найти косинус угла между 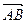 и
и 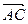 , если
, если 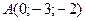 ;
; 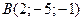 ;
; 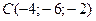 . Сделать чертеж.
. Сделать чертеж.
1.1.9. Найти угол между 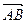 и
и 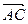 , если
, если 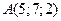 ;
; 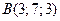 ;
; 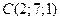 . Сделать чертеж.
. Сделать чертеж.
1.1.10. Найти угол между 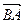 и
и 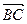 , если
, если 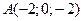 ;
; 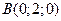 ;
; 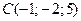 . Сделать чертеж.
. Сделать чертеж.
2.1.11.Уравнение одной из сторон квадрата х+3у–5= 0. Составить уравнения трех остальных сторон квадрата, если Р(–1; 0) – точка пересечения его диагоналей. Сделать чертеж.
2.1.12.Даны уравнения одной из сторон ромба х–3у+10=0 и одной из ее диагоналей х+4у–4=0; диагонали ромба пересекаются в точке Р(0; 1). Найти уравнения остальных сторон ромба. Сделать чертеж.
2.1.13.Уравнения двух сторон параллелограмма х+2у+2=0 и х+у–4=0, а уравнение одной из его диагоналей х–2=0. Найти координаты вершин параллелограмма. Сделать чертеж.
2.1.14.Даны две вершины А(–3; 3) и В(5; –1) и точка D(4; 3) пересечения высот треугольника. Составить уравнения его сторон. Сделать чертеж.
2.1.15.Даны вершины А(3; –2), В(4; –1), С(1; 3) трапеции ABCD (AD || BC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж.
2.1.16.Даны уравнения двух сторон треугольника 5х–4у+15=0 и
4х+у–9=0. Его медианы пересекаются в точке Р(0; 2). Составить уравнение третьей стороны треугольника. Сделать чертеж.
2.1.17.Даны две вершины А(2; –2) и В(3; –1) и точка Р(1; 0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С. Сделать чертеж.
2.1.18.Даны уравнения двух высот треугольника х+у=4 и у=2х и одна из его вершин А(0; 2). Составить уравнения сторон треугольника. Сделать чертеж.
2.1.19.Даны уравнения двух медиан треугольника х–2у+l = 0 и у–1=0 и одна из его вершин А(1; 3). Составить уравнения его сторон. Сделать чертеж.
2.1.20.Две стороны треугольника заданы уравнениями 5х–2у–8=0 и
3х–2у–8=0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны. Сделать чертеж.
2.2.11. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
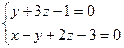
а) 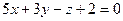 ; б)
; б) 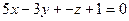 ; в)
; в) 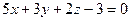 ;
;
г) 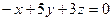 ; д)
; д) 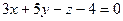 .
.
Сделать схематический чертеж.
2.2.12. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
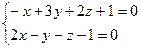
а) 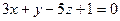 ; б)
; б) 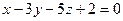 ; в)
; в) 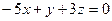 ;
;
г) 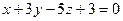 ; д)
; д) 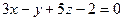 .
.
Сделать схематический чертеж.
2.2.13. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
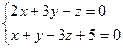
а) 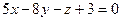 ; б)
; б) 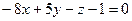 ; в)
; в) 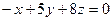 ;
;
г) 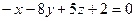 ; д)
; д) 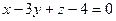 .
.
Сделать схематический чертеж.
2.2.14. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
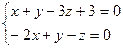
а) 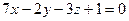 ; б)
; б) 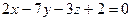 ; в)
; в) 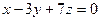 ;
;
г) 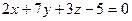 ; д)
; д) 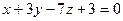 .
.
Сделать схематический чертеж.
2.2.15. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
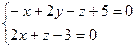
а) 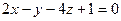 ; б)
; б) 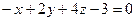 ; в)
; в) 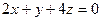 ;
;
г) 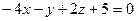 ; д)
; д) 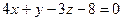 .
.
Сделать схематический чертеж.
2.2.16. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
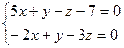
а) 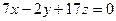 ; б)
; б) 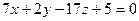 ; в)
; в) 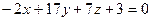 ;
;
г) 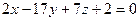 ; д)
; д) 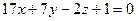 .
.
Сделать схематический чертеж.
2.2.17. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
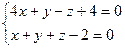
а) 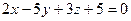 ; б)
; б) 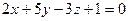 ; в)
; в) 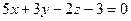 ;
;
г) 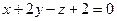 ; д)
; д) 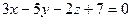 .
.
Сделать схематический чертеж.
2.2.18. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
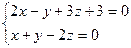
а) 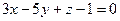 ; б)
; б) 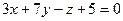 ; в)
; в) 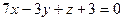 ;
;
г) 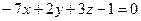 ; д)
; д) 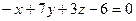 .
.
Сделать схематический чертеж.
2.2.19. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
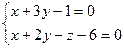
а) 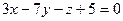 ; б)
; б) 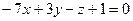 ; в)
; в) 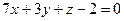 ;
;
г) 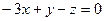 ; д)
; д) 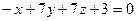 .
.
Сделать схематический чертеж.
2.2.20. Указать какой из данных плоскостей а); б); в); г); д) перпендикулярна прямая:
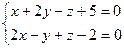
а) 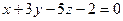 ; б)
; б) 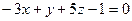 ; в)
; в) 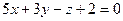 ;
;
г) 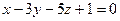 ; д)
; д) 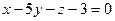 .
.
Сделать схематический чертеж.
3.1.41–3.1.70. Решить систему линейных уравнений матричным методом и методом Гаусса. Сделать проверку.
3.1.41. 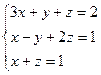 3.1.42.
3.1.42. 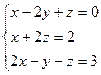
3.1.43. 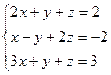 3.1.44.
3.1.44. 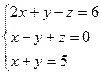
3.1.45. 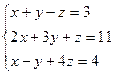 3.1.46.
3.1.46. 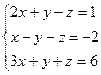
3.1.47. 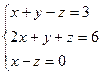 3.1.48.
3.1.48. 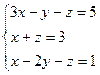
3.1.49. 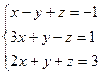 3.1.50.
3.1.50. 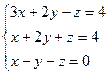
Введение в математический анализ.
Производная и ее приложения.
6.2.31–6.2.40. Найти пределы функций, не пользуясь правилом Лопиталя.
6.2.31. а) 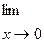
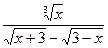 ; б)
; б) 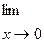
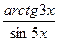 ;
;
в) 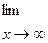
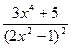 ; г)
; г) 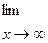
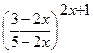 .
.
6.2.32. а) 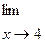
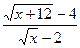 ; б)
; б) 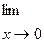
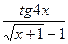 ;
;
в) 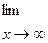
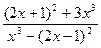 ; г)
; г) 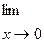
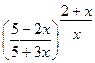 .
.
6.2.33. а) 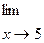
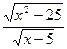 ; б)
; б) 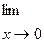
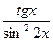 ;
;
в) 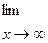
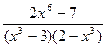 ; г)
; г) 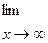
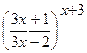 .
.
6.2.34. а) 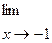
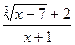 ; б)
; б) 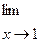
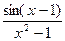 ;
;
в) 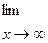
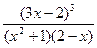 ; г)
; г) 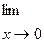
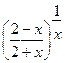 .
.
6.2.35. а) 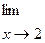
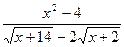 ; б)
; б) 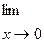
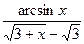 ;
;
в) 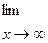
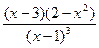 ; г)
; г) 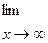
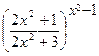 .
.
6.2.36. а) 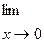
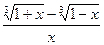 ; б)
; б) 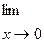
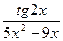 ;
;
в) 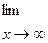
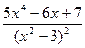 ; г)
; г) 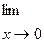
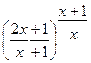 .
.
6.2.37. а) 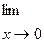
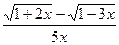 ; б)
; б) 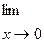
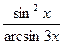 ;
;
в) 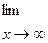
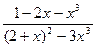 ; г)
; г) 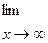
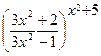 .
.
6.2.38. а) 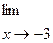
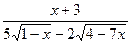 ; б)
; б) 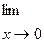
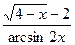 ;
;
в) 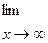
 ; г)
; г) 
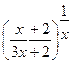 .
.
6.2.39. а) 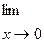
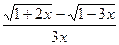 ; б)
; б) 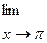
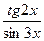 ;
;
в) 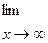
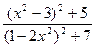 ; г)
; г) 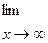
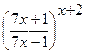 .
.
6.2.40. а) 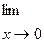
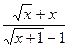 ; б)
; б) 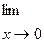
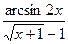 ;
;
в) 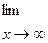
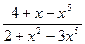 ; г)
; г) 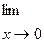
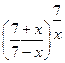 .
.
6.3.11–6.3.20. Задана функция у= f (х). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж.
6.3.11. 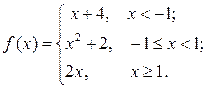
6.3.12. 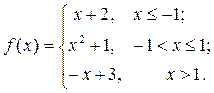
6.3.13. 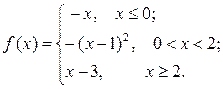
6.3.14. 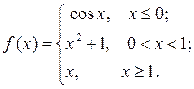
6.3.15. 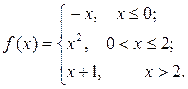
6.3.16. 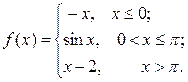
6.3.17. 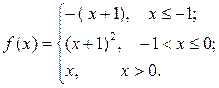
6.3.18. 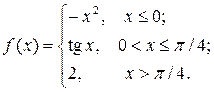
6.3.19. 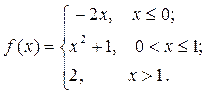
6.3.20. 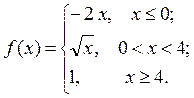
7.1.1–7.1.10. Найти производные 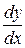 данных функций.
данных функций.
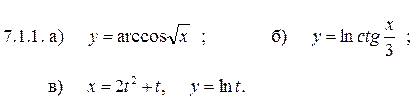
7.1.2. 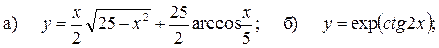
в) 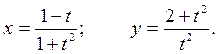
7.1.3. а) 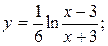 б) y = arcctg [exp(5x)] ;
б) y = arcctg [exp(5x)] ;
в) x = sin23t, y = cos23t .
7.1.4. 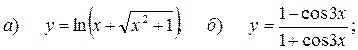
в) x = t4 + 2t, y = t2 + 5t .
7.1.5. 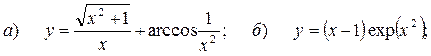
в) x = t – ln sint, y = t + ln cost .
7.1.6. a) 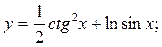 б) y = exp(cos3x) .
б) y = exp(cos3x) .
в) x = tg t , 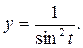
7.1.7. a) 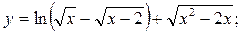 б) y = 3x exp(-x-2) ;
б) y = 3x exp(-x-2) ;
в) x = t2 – t3 , y = 2t3 .
7.1.8. a) y = ln cos2x – ln sin2x ; б) 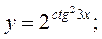
в) x = cos3t , y = sin3t .
7.1.9. a) 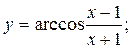 б)
б) 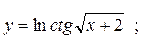
в) x = 3sint, y = 3cos2t .
7.1.10. 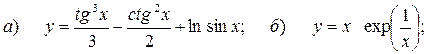
в) x = 2t – t2 , y = 2t3 .
7.3.21–7.3.30. Методами дифференциального исчисления: а) исследовать функцию y = f (x) для 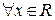 и по результатам исследования построить ее график; б) Найти наименьшее и наибольшее значения заданной функции на отрезке [a; b].
и по результатам исследования построить ее график; б) Найти наименьшее и наибольшее значения заданной функции на отрезке [a; b].
7.3.21. а) 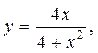 б) [–3; 3] .
б) [–3; 3] .
7.3.22. а) 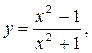 б) [–1; 1] .
б) [–1; 1] .
7.3.23. а) 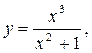 б) [–2; 2 ] .
б) [–2; 2 ] .
7.3.24. а) 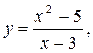 б) [–2; 2] .
б) [–2; 2] .
7.3.25. а) 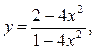 б) [ 1; 4] .
б) [ 1; 4] .
7.3.26. а) 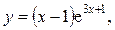 б) [ 0; 1] .
б) [ 0; 1] .
7.3.27. а) 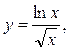 б) [ 1; 9] .
б) [ 1; 9] .
7.3.28. а) 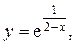 б) [–1; 1] .
б) [–1; 1] .
7.3.29. а) 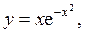 б) [–2; 2] .
б) [–2; 2] .
7.3.30. а) 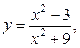 б) [–2; 2] .
б) [–2; 2] .
Дата добавления: 2023-01-08; просмотров: 84; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
