Определенный интеграл с переменным верхним
Замечание о неберущихся интегралах
Имеется большая группа интегралов, которые не выражаются через элементарные функции. Вот некоторые из них:
1) Интеграл вероятностей: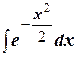 
.
2) Интегральный логарифм: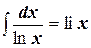 
.
3) Интегральный синус: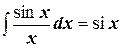 
.
4) Интегральный косинус: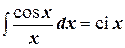 
.
5) Интегралы Френеля: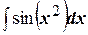 
и 
.
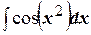6) Большей частью не берутся интегралы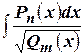 
, если 
.
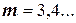Задача о вычислении площади криволинейной
Трапеции
Пусть функция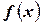 
непрерывна на отрезке 
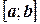и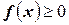 
. Рассмотрим фигуру, ограниченную графиком 
, отрезком 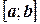оси абсцисс и линиям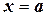и 
и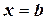 
. Такую фигуру назовём криволинейной трапецией (рис. 4.3).
Рис. 4.3.
Вычислим площадь этой фигуры. Для этого точками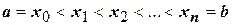 
разобьем отрезок 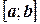на частичные отрезки 
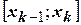и обозначим 
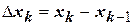. Для каждого отрезка 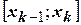выберем произвольную точку 
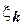и построим прямоугольник с основанием 
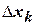и высотой 
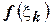как показано на рисунке. Площадь такого прямоугольника будет равна 
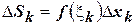. А площадь всей фигуры соответственно 
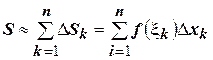. Это равенство будет тем точнее, чем на большее количество отрезков 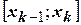разбит отрезок 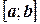, то есть 
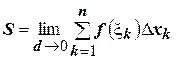(где 
).
К необходимости вычисления таких пределов приводит целый ряд других задач, таких как вычисление длины линии, вычисление объема тела, вычисление площади поверхности вращения, вычисление работы и др.
Определенный интеграл и его свойства
Пусть на отрезке 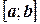задана непрерывная функция 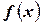. Разобьем точками 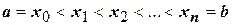отрезок 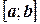на частичные отрезки 
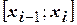и примем 
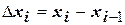. На каждом частичном отрезке выберем точку 
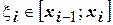. Сумму
|
|
|
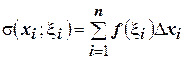(4.21)
называют интегральной суммой, соответствующей данному способу разбиения отрезка 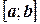на части и данному способу выбора точек 
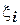на каждом из частичных отрезков.
Если существует предел суммы (4.21), не зависящий от способа разбиения отрезка 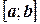и способа выбора точек 
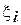, то его называют определенным интегралом от функции 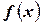по отрезку 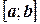и записывают
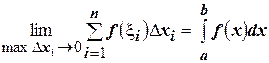. (4.22)
Справедливо утверждение: если функция 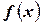непрерывна на 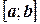, то определенный интеграл 
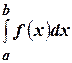всегда существует.
Замечание:
1). Вообще – то интеграл (4.22) существует и при менее жестких требованиях, накладываемых на функцию 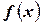. Однако в нашем курсе будем предполагать, что функция 
.
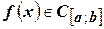2). В соответствии с (4.22) площадь криволинейной трапеции (см. п. 4.14) вычисляется по формуле
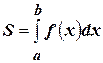(4.23)
Отметим основные свойства определённых интегралов:
1) 
Доказательство:
Так как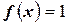 
, то интегральная сумма для интеграла 
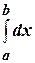примет вид 
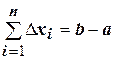. Переходя к пределу, получим
. ☻
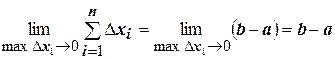2) 
, где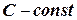 
.
Доказательство:
Составим интегральную сумму и перейдем к пределу: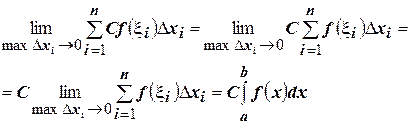 
☻
|
|
|
3) Если существуют 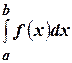и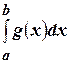 
, то существует и 
.
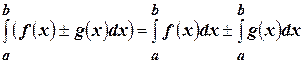Доказательство:
Составим интегральную сумму для интеграла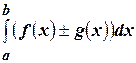 
и перейдем в ней к пределу. Получим
☻
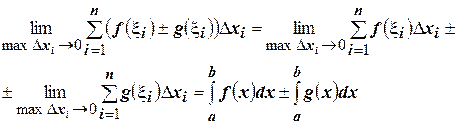4) По соглашению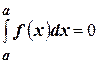 
5) По соглашению 
6) Если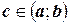 
, то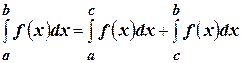 
.
Доказательство:
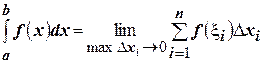
Поскольку этот предел не зависит от способа разбиения отрезка 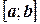, то возьмем такой способ разбиения, чтобы точка 
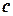была одной из точек разбиения отрезка 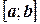. Тогда:
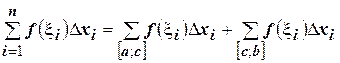
И переходя к пределу, получим:
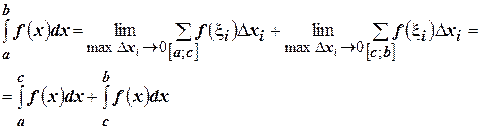
Это свойство остаётся в силе и при любом расположении точек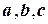 
.
Например, если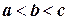 
и функция 
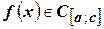, то
. ☻
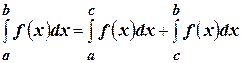7) Если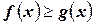 
, то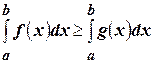 
, причем равенство будет только в том случае, если 
.
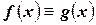Доказательство:
Имеем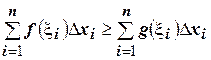 
, т.к. слагаемые в сумме, стоящей в левой части неравенства, не меньше соответствующих слагаемых правой суммы. Переходя к пределу в неравенстве, получим требуемый результат. ☻
8) Если 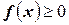, то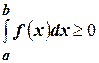 
,
а если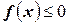 
, то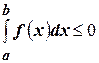 
.
Это свойство определённых интегралов является следствием предыдущего свойства.
9) 
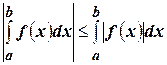
Доказательство:
Проинтегрируем неравенство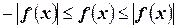 
и получим
,
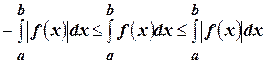что как раз и означает, что
.☻
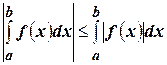Теорема о среднем значении
Теорема о среднем значении: Пусть функци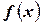и и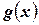 
непрерывны на отрезке 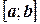и 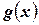знакопостоянна на этом отрезке. Тогда 
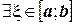, такая что
|
|
|
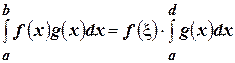. (4.24)
Доказательство:
Пусть для определённости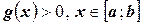 
. Функция 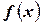на отрезке 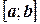удовлетворяет условиям теоремы Вейерштрасса. Следовательно, на этом отрезке она достигает своих наибольшего и наименьшего значений, т. е. 
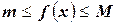. Умножим это неравенство на 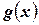. В результате получим 
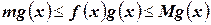. Теперь проинтегрируем это неравенство:
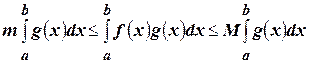. (4.25)
Анализируя (4.25), приходим к выводу, что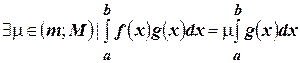 
. По теореме о принятии функцией, непрерывной на отрезке, любого промежуточного значения: 
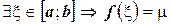. Подставим вместо 
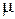значение 
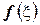, получим
. ☻
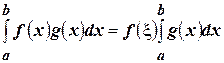Замечания:
1). Если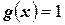 
, то соотношение (4.24) принимает вид
.
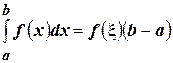Следовательно,
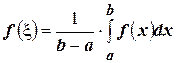. (4.26)
Значение функции 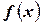, вычисленное по формуле (4.26), принято называть средним значением функции 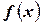на отрезке .
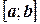2). Если 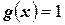, то неравенство (4.25) принимает вид
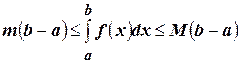. (4.27)
Неравенство (4.27) может использоваться для оценки значения определённого интеграла. Например, требуется оценить значение интеграла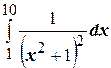 
. Легко определить, что наибольшее на отрезке 
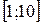значение подынтегральной функции равно 0,25, а наименьшее - 
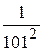. Поэтому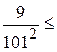 
.
|
|
|
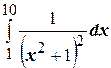
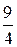Определенный интеграл с переменным верхним
Пределом. Теорема Барроу
Пусть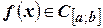 
и 
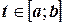. Рассмотрим определённый интеграл с переменным верхним пределом
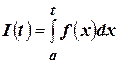. (4.28)
Теорема Барроу: Интеграл (4.28) является первообразной для подынтегральной функции, т.е.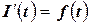 
.
Доказательство:
По определению производной:
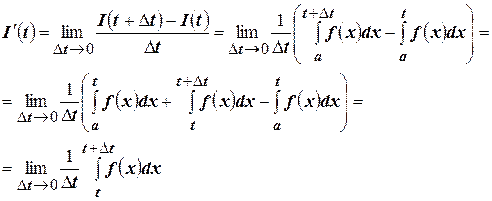
Воспользуемся теоремой о среднем значении:
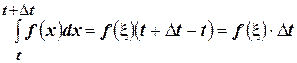
Так как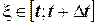 
, то пр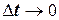и 
и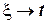 
. Тогда
,
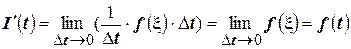что и требовалось доказать. ☻
Замечание:
Пусть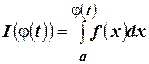 
, тогда по теореме о дифференцировании сложной функции 
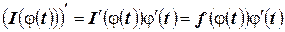. Например, производная от интеграла 
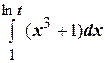равна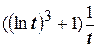 
.
Формула Ньютона-Лейбница
Пусть 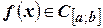и 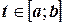. И пусть 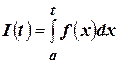. Если функция 
- некоторая первообразная для подынтегральной функции, то по теореме об общем виде первообразных: 
. Положим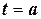 
, тогда 
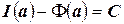. Но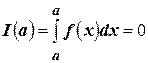 
, следовательно, 
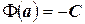. Получили соотношение 
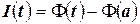. Положим теперь в этом выражении 
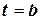. В итоге получаем формулу
. (4.29)
Формулу (4.29) называют формулой Ньютона-Лейбница. Эта формула является основной при вычислении определённых интегралов.
Пример: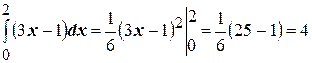 
Дата добавления: 2022-12-03; просмотров: 36; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!