Исследуем количество решений уравнения с параметром самостоятельно.

⇐ ПредыдущаяСтр 2 из 2

А теперь я предлагаю вам решить следующую задачу на исследование числа решений уравнения с параметром самостоятельно. Однако я не брошу вас на “произвол судьбы”, мы будем работать вместе с вами следующим образом. Я разобью решение задачи на несколько этапов и буду формулировать цель, которую вы должны достичь на очередном этапе решения. Вы пробуете эту цель реализовать. Получается – хорошо, не получается – смотрите (подглядывайте) в мое решение и снова продолжайте решать задачу самостоятельно.

Итак, начали!

Задача 3. Определите, сколько корней в зависимости от значения параметра a имеет уравнение

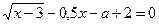Первый этап.

Сначала нужно представить исходное уравнение в виде

f(x) = g(x),

где в записи формулы функции f(x) не содержится параметр, а в записи формулы функции g(x), наоборот, содержится.

Мое решение.

Исходное уравнение можно переписать следующими способами:

(1): 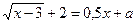, тогда , .

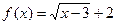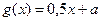(2): 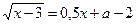, тогда , .

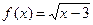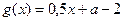(3): 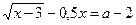, тогда , .

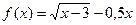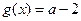Последний вариант явно не подходит, так как построить график функции 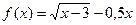проблематично. Варианты (1) и (2) равноценны. Лично я предпочту выбрать первый из них.

Второй этап.

Теперь нужно построить график функции y = f(x) и представить, как будет выглядеть график функции y = g(x) при конкретном значении параметра a, что будет с этим графиком происходить, если значение параметра a будет изменяться.

Мое решение.

График функции 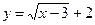изображен на рис. 8. Он получается при параллельном переносе графика функции 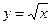на 3 единицы вправо и 2 единицы вверх.

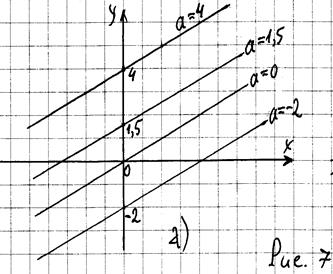
На рис. 7(а) показан график функции 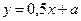для некоторых значений параметра а. По поводу этого графика можно сказать следующее:

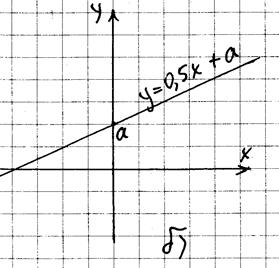
1. При конкретном значении a график функции 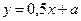является прямой с угловым коэффициентом 0,5, пересекающей ось y в точке с ординатой a (см. рис. 7(б)).

2. С увеличением значения параметра a прямая 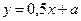смещается параллельно вверх, с уменьшением значения параметра a эта прямая смещается параллельно вниз.

Третий этап.

Построим графики функций y = f(x) и y = g(x) в одной системе координат. Для каждого возможного расположения параметрического графика y = g(x) определим число его общих точек с графиком функции y = f(x).

Мое решение.

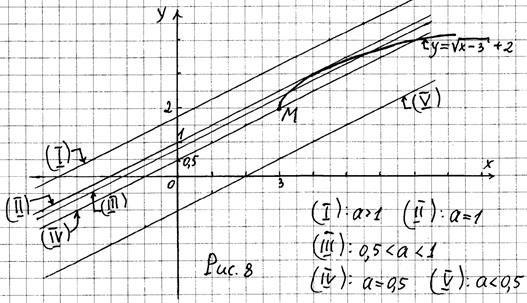
Прямая 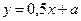может занимать пять основных положений (см. рис. 8):

( I) – в этом положении прямая лежит выше графика функции 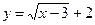и не имеет с ним общих точек;

( II) – в этом положении прямая касается графика функции 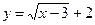и имеет с ним одну общую точку;

( III) и ( IV) – в этом положении прямая и график функции 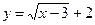имеют две общие точки;

( V) – в этом положении прямая пересекает график функции 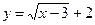в одной точке, то есть имеет с ним одну общую точку.

Четвертый этап.

Выделяем особые расположения параметрического графика y = g(x). Определяем значения параметра a, при которых график функции y = g(x) эти положения занимает.

Мое решение.

Прямая 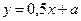может занимать два особых положения: ( II) и ( IV).

Сначала определим значение параметра a, при котором прямая 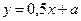занимает положение ( II). Здесь ключевым моментом является то, что при таком расположении прямая касается графика функции .

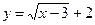Пусть x и y – координаты точки касания прямой с графиком функции 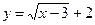. Найдем значения x, y и a из системы уравнений:

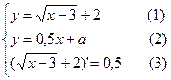Уравнения (1) и (2) системы означают, что точка касания принадлежит обоим графикам, то есть является их общей точкой. А вот уравнение (3) выражает геометрический смысл производной:

производная функции в некоторой точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Итак, начинаем решение системы с уравнения (3):

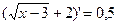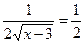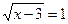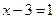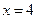Теперь подставляя 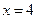в уравнение (1), получим:

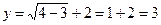Таким образом, мы нашли координаты точки касания: 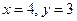. Подставляя далее эти координаты в уравнение (2), находим значение параметра a:

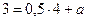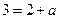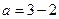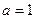Итак, прямая 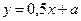занимает положение ( II) при .

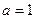Теперь нужно найти значение параметра a, при котором прямая 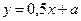занимает положение ( IV). Здесь ключевым моментом является то, что при таком расположении прямая проходит через начальную точку М (3; 2) графика функции .

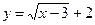Подставляя в уравнение прямой координаты точки М, находим значение параметра a:

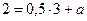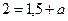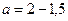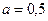Таким образом, прямая 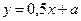занимает положение ( IV) при .

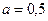Пятый этап.

Определяем значения параметра a, при которых график функции y = g(x) занимает положения, не вошедшие в число особых.

Мое решение.

Здесь можно исходить из следующего свойства параметрического графика:

прямая 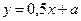пересекает ось y в точке с ординатой, равной a.

Ордината точки пересечения прямой 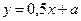с осью y в положении ( I) больше, чем в положении ( II). Следовательно, эта прямая занимает положение ( I) при значениях параметра .

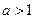Аналогично этому определяем, что прямая 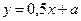занимает положение ( III) при значениях параметра 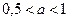и положение ( V) при значениях параметра .

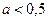Шестой (заключительный) этап.

Собирая полученные ранее результаты воедино, даем к задаче ответ.

Теперь осталось вспомнить, что количество общих точек графиков 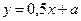и 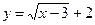равно числу корней исходного уравнения с параметром, и написать ответ к задаче.

Ответ: уравнение не имеет решений при 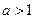; имеет один корень при 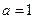, 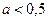; имеет два корня при .

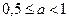Заключение.

Давайте же вспомним, что мы узнали в процессе изучения данного пособия и чему научились.

● Сначала мы узнали, что такое параметр и что такое задача с параметром, а также приобрели поверхностное представление о том, как решаются задания с параметром аналитическим способом.

● Далее мы познакомились с графическим методом решения обычного (не содержащего параметр) уравнения вида f(x) = g(x).

● И, наконец, мы довольно подробно познакомились с тем, как, применяя графический способ, находить число корней параметрического уравнения в зависимости от значений параметра.

Конечно, полученных вами в процессе изучения данного пособия знаний ещё недостаточно для того, чтобы справиться с экзаменационной задачей с параметром, и даже для того, чтобы решать некоторые задания с параметром более низкого уровня сложности, чем данная экзаменационная задача. Но продолжайте изучать методы решения заданий с параметром самостоятельно (по книгам), на курсах или в контакте с преподавателем. Добивайтесь ответа на любой, даже самый незначительный вопрос. И тогда вам будет сопутствовать удача.

Желаю успехов!

Литература для изучения методов решения задач с параметрами
на начальном этапе (с комментариями).

Ниже дается список книг, по которым, по мнению автора, проще изучать методы решения задач с параметрами на начальном этапе:

[1]. Алгебра. Нестандартные задачи. Экспресс-репетитор для подготовки к ГИА. 9-й кл. / Г.В. Сычёва, Н.Б. Гусева, В.А. Гусев. – М.: Астрель, 2010 (и более поздние издания).

[2]. Сборник задач по алгебре: учебное пособие для 8-9 классов с углубленным изучением математики / М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич.

В книге [1] приводится множество примеров решений несложных заданий с параметром. Даются задания для самостоятельной работы, к которым приводится решение.

Книга [2] – это сборник задач. При помощи таблицы, приведенной на следующей странице, вы сможете быстро найти в этом сборнике подходящие упражнения на каждый тип заданий с параметром.

К сборнику вышел решебник.

Тип задания	Номера упражнений
Определение количества решений уравнения с параметром.	9.18-9.21 9.39-9.45
Решение квадратного уравнения с параметром путем подбора его корней.	5.32-5.34 5.77
Решение уравнений с параметром, сводящихся к квадратному.	5.68 9.13
Соотношение между переменными. Разложение на множители.	5.35-5.36 8.5, 8.9-8.10
Дробно-рациональное уравнение с параметром.	5.60
Задачи на исследование линейного уравнения с параметром.	6.150-6.153
Системы линейных уравнений с параметром и задачи к ним сводящиеся.	9.101-9.107
Задачи на исследование систем линейных уравнений с параметром.	6.179-6.181
Системы нелинейных уравнений с параметром и задачи к ним сводящиеся.	9.119-9.120 9.195-9.215
Линейное неравенство с параметром.	6.143 6.200
Исследование системы линейных неравенств с параметром.	6.158-6.163
Простейшее исследование квадратного уравнения с параметром.	6.146-6.148 6.225-6.226
Задачи на расположение корней квадратного трехчлена на координатной прямой.	6.170-6.178 8.42-8.46 8.110 8.117-8.119 8.126
Задачи на расположение чисел, заданных в параметрической форме, на координатной прямой.	8.92-8.95
Исследование квадратного неравенства с параметром.	8.111-8.112
Решение квадратного или дробно-рационального неравенства с параметром.	8.113-8.115
Разные задачи на квадратное неравенство с параметром.	6.224, 6.230 8.56, 8.64-8.71 8.116, 8.120-8.125
Решение неравенства с параметром методом интервалов.	6.231 8.115
Решение иррациональных уравнений и неравенств с параметром.	11.133 11.147

Дата добавления: 2022-11-11; просмотров: 64; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!