Решение заданий с параметром графическим методом.

Об авторе.

Автор данного пособия – опытный репетитор по математике, школьный учитель. Закончил физический факультет МГУ и физико-математическую школу им. А. Н. Колмогорова (ныне СУНЦ при МГУ).

Им написано множество хороших пособий по математике, одно из которых издано в форме книги:

Волков Д.А. ЕГЭ по математике. Практическая подготовка к заданию С3. – М.:ИЛЕКСА, 2014.

В данном пособии излагаются некоторые ключевые моменты, связанные с решением задач с параметром, не поняв которые вряд ли можно рассчитывать на успешное решение этого задания на экзамене. Именно поэтому автор предпочел привести разбор решений всего нескольких задач, но с подробным описанием применяемых идей (как это обычно делается на репетиторских занятиях), вместо того, чтобы писать краткое решение множества задач (как это делается в большинстве пособий по математике), полагая, что читатель до всего несказанного додумается сам.

Пособие адресовано старшеклассникам, готовящимся к ЕГЭ, учащимся физико-математических классов и преподавателям математики.

Содержание документа:

Предисловие автора. – стр. 1

Что такое параметр. Аналитический метод решения заданий с параметром. – стр. 2

Графический метод решения уравнения вида f( x) = g( x). – стр. 2-3

Решение заданий с параметром графическим методом. – стр. 3-5

Использование геометрического смысла производной при решении заданий с параметром. – стр. 5-7

Исследование количество решений уравнения с параметром. Общий случай. – стр. 7-8

Особые расположения графика с параметром при исследовании параметрического уравнения. – стр. 9

Исследуем количество решений уравнения с параметром самостоятельно. – стр. 7-12

Заключение. – стр. 12

Литература для изучения методов решения задач с параметрами на начальном этапе (с комментариями). – стр. 12

Предисловие автора.

Задача с параметром – одна из самых сложных в ЕГЭ по математике. Такие задачи, как правило, не проходят в общеобразовательных школах (или проходят очень поверхностно). Материал, относящийся к заданиям с параметром, изучается в основном в физико-математических школах. Поэтому неудивительно, когда даже сильные учащиеся общеобразовательных классов, занимающиеся на подготовительных курсах по математике, плохо воспринимают на них материал по задаче с параметром, в то время как материал по другой сложной задаче ЕГЭ – задаче по планиметрии – ими может восприниматься отлично.

Занимаясь подготовкой к ЕГЭ по математике учащихся общеобразовательных классов, я разработал целую систему обучения задачи с параметром с “нуля”, то есть в предположении, что ученик вообще не имеет понятия о задачах с параметром и как их решать. Часть этой системы (притом крошечная) и отражена в предлагаемом вашему вниманию пособии.

Однако я уверен, что даже эта крошечная часть поможет многим читателям узнать и понять самое существенное о задачах с параметром и методах их решения. А, имея в своем сознании это существенное, читатель в дальнейшем уже быстро и осмысленно сможет продолжить изучение материала по методам решения задания с параметром любым удобным ему способом.

Прежде чем изучать методы решения заданий с параметром, разумеется, нужно разобраться в том, что означают термины “параметр” и “задача с параметром”. Это мы и выясним в следующем пункте.

Что такое параметр. Аналитический метод решения заданий с параметром.

Для того чтобы понять, что такое задача с параметром и что такое параметр, разберем конкретный пример.

Рассмотрим обычную задачу: решить уравнение 3х = 2. После деления обеих частей уравнения на 3 получим ответ: х = 2/3.

Теперь заменим коэффициент 3 при переменной х буквой а и решим уравнение aх = 2, предполагая, что буква a обозначает какое-то известное число. После деления обеих частей уравнения на а получим х = 2/а. Однако выполнять деление обеих частей уравнения на a можно лишь при a ≠ 0. Поэтому случай a = 0 придется рассмотреть отдельно: тогда уравнение принимает вид 0х = 2 и не имеет решений. Итак, уравнение не имеет решений при a = 0 и имеет решение х = 2/a при a ≠ 0.

Буква, обозначающая в математической задаче известное число (то есть, буква, значение которой предполагается заданным), называется параметром. Задача же в этом случае будет называться задачей с параметром.

Решение задачи с параметром, как правило, связано с грамотным перебором возможных значений параметра.

Пусть, например, требуется решить неравенство с параметром: (а – 2)х < –5. Решать линейное неравенство мы привыкли путем деления его обеих частей на коэффициент при переменной х, который в данном случае равен а – 2. Но, если этот коэффициент равен нулю, то делить на него обе части неравенства нельзя. Таким образом, придется рассмотреть два случая: а – 2 = 0 и а – 2 ≠ 0. Пусть теперь а – 2 ≠ 0. Тогда вспомним, что при делении обеих частей неравенства на положительное число знак неравенства сохраняется, а при делении на отрицательное число – меняется на противоположный. Значит, случай а – 2 ≠ 0 разбивается ещё на два: а – 2 > 0 и а – 2 < 0.

Итак, у нас получились три варианта возможных значений параметра. Для каждого из этих вариантов получим ответ.

1. а – 2 = 0, то есть a = 2.

Тогда неравенство приобретает вид 0х < –5 и не имеет решений.

2. а – 2 > 0, то есть a > 2.

Тогда после деления обеих частей неравенства на положительное число а – 2 получаем х < –5/(а – 2).

3. а – 2 < 0, то есть a < 2.

Тогда после деления обеих частей неравенства на отрицательное число а – 2 получаем х > –5/(а – 2).

Окончательный ответ к задаче собирается из ответов, полученных при рассмотрении каждого из случаев. К каждому ответу обязательно указываются соответствующие ему значения параметра.

Ответ: если a = 2, то решений нет; если a > 2, то 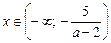; если a < 2, то .

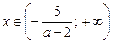При решении уравнения с параметром aх = 2 и неравенства с параметром (a – 2)х < –5 мы применили аналитический метод, то есть выполняли вычисления и алгебраические преобразования, не опираясь на графические построения. Однако при решении многих задач с параметром принято опираться на графические построения, так как это существенно облегчает решение. Знакомство с графическим методом решения заданий с параметром и является нашей главной целью.

Графический метод решения уравнения вида
f( x) = g( x).

Графический метод решение уравнения вида f(x) = g(x) основывается на следующем утверждении.

Пусть в системе координат построены графики функций y = f(x) и y = g(x) . Тогда абсциссы общих точек этих графиков являются корнями уравнения f(x) = g(x). Если же графики функций y = f(x) и y = g(x) не имеют общих точек, то уравнение f(x) = g(x) не имеет решений.

Не будем доказывать данное утверждение ввиду его очевидности, а сразу рассмотрим пример его практического применения.

Предположим, требуется найти корни уравнения

x² = – 2x +3.

Графический метод решения этого задания предполагает следующее:

1) строим в одной системе координат графики функций y = x² и y = – 2x +3 (см. рис. 1);

2) видим, что эти графики пересекаются в точках (– 3; 9) и (1; 1);

3) тогда абсциссы этих точек, то есть числа x = – 3 и x = 1, и будут корнями исходного уравнения.

Правильность найденных корней можно проверить путем непосредственной подстановки их в уравнение.

Уже при решении этого примера видны недостатки графического метода. Во-первых, этот метод предполагает, что графики функций y = f(x) и y = g(x) имеют “хорошие” общие точки, то есть такие, которые можно точно построить в системе координат. Во-вторых, малейшие неточности при построении графиков функций y = f(x) и y = g(x) могут привести к тому, что они не пересекутся в нужной точке, а пересекутся где-то поблизости от нее.

Однако у графического метода решения уравнения вида f(x) = g(x) есть одно несомненное преимущество: при помощи этого метода можно увидеть, имеет ли данное уравнение корни или, наоборот, не имеет их; в том же случае, когда уравнение имеет корни, можно сосчитать их количество. При этом необязательно строить графики функций y = f(x) и y = g(x) точно, достаточно построить их эскизы.

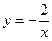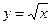Так, построив эскизы графиков функций и , можно увидеть, что они не пересекаются, а это значит, что уравнение

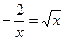
не имеет решений. Выполните соответствующие построения самостоятельно.

Решение заданий с параметром графическим методом.

Теперь давайте посмотрим, как рассмотренный в предыдущем пункте графический метод решения уравнения вида f(x) = g(x) применяется при решении следующей задачи с параметром.

Задача 1. Определите, при каких значениях параметра a уравнение

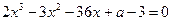
имеет ровно два корня.

Решение.

Перепишем уравнение в виде

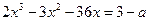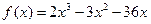
Введем две функции:

Тогда исходное уравнение можно переписать в виде

f(x) = g(x)

и переформулировать задачу в равносильной форме:

определите, при каких значениях параметра a графики функций f(x) и g(x) имеют ровно две общие точки.

Задача в последней формулировке уже подразумевает графический метод решения, так как требует построение графиков функций.

Пусть вас не смущает, что в записи формулы функции g(x) не написана явно переменная х, эту переменную можно ввести в запись функции искусственно:

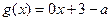Однако функция g(x) смущает наличием в записи ее формулы параметра а. Поэтому давайте посмотрим, как выглядит формула функции для конкретных значений параметра:

Значение параметра а	Вид функции y = 3 – а
– 3	y = 6
0,5	y = 2,5
3	y = 0
5	y = – 2
8,5	y = – 5,5

Итак, всё прояснилось: функция y = 3 – а при известном значении параметра a принимает постоянное значение (такая функция называется константой), а графиком этой функции является горизонтальная прямая.

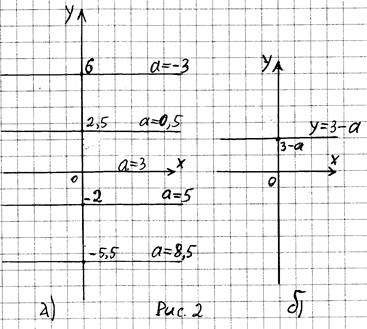
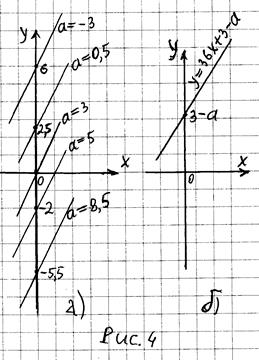
На рис. 2 (а) показан график функции y = 3 – a для значений параметра a, взятых из выше приведенной таблицы. По поводу этого графика можно сказать следующее:

1. При конкретном значении a график функции y = 3 – a является горизонтальной прямой, пересекающей ось y в точке с ординатой 3 – a (см. рис. 2(б))

2. С увеличением значения параметра a прямая y = 3 – a смещается параллельно вниз, с уменьшением значения параметра a эта прямая смещается параллельно вверх.

Последнее утверждение связано с тем, что при увеличении значения a значение выражения 3 – a уменьшается, и, обратно, при уменьшении значения a значение выражения 3 – a увеличивается.

Эскиз графика функции (он изображен на рис. 3) нетрудно получить, проведя исследование этой функции при помощи производной. Характерными токами графика являются: точка максимума А (– 2; 44) и точка минимума В (3; – 81). Ещё можно заметить, что график функции проходит через начало системы координат О (0; 0).

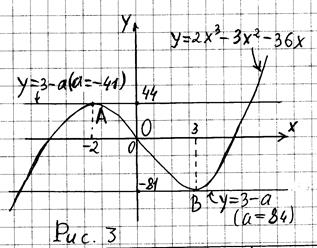
Изобразив прямую y = 3 – а в различных положениях (см. рис. 6), можно увидеть, что она имеет с графиком функции ровно две общие точки только в том случае, если проходит или через точку А, или через точку В.

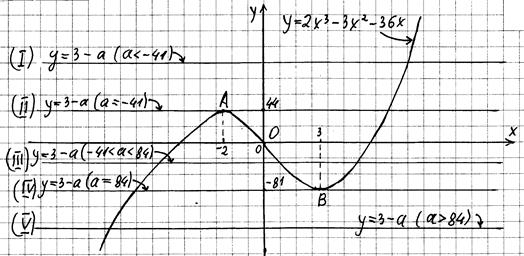
Рис. 6

Если эта прямая проходит через точку А, то выполнятся равенство

3 – а = 44

(это равенство означает, что ордината точки пересечения прямой y = 3 – а с осью y равна ординате точки А, то есть числу 44). Из равенства находим:

а = – 41.

Если же прямая проходит через точку А, то выполнятся равенство

3 – а = – 81,

(это равенство означает, что ордината точки пересечения прямой y = 3 – а с осью y равна ординате точки В, то есть числу – 81). Из равенства находим:

а = 84.

Итак, при a = – 41 или a = 84 графики функци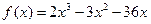й и имеют ровно две общие точки, а значит уравнение

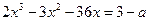
и равносильное ему уравнение

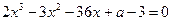
имеют ровно два корня.

Задача решена.

Ответ: a = – 41, а = 84.

Использование геометрического смысла производной
при решении заданий с параметром.

При решении задачи 1 уравнение с параметром

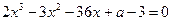
можно было переписать и в другом виде, например, таком:

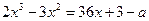Тогда нам придется ввести две функции

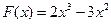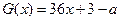
и найти значения параметра а, при каждом из которых графики этих функций имеют ровно две общие точки.

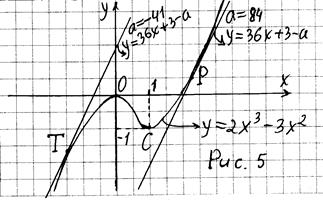
Эскиз графика функции 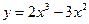(он изображен на рис. 5) нетрудно получить, проведя исследование этой функции при помощи производной. Характерными точками графика являются: точка максимума О (0; 0) и точка минимума С (1; – 1).

Чтобы узнать, что представляет собой функция 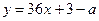, посмотрим, как выглядит её формула для конкретных значений параметра:

Значение параметра а	Вид функции y = 36х + 3 – а
–3	y = 36х + 6
0,5	y = 36х + 2,5
3	y = 36х
5	y = 36х – 2
8,5	y = 36х – 5,5

Итак, функция 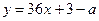является линейной. При этом ее угловой коэффициент постоянен и равен числу 36, а свободный коэффициент, равный 3 – a, зависит от значения параметра a (напомню, что линейной называется функция вида y = kx + b, при этом число k называется угловым коэффициентом, а число b – свободным коэффициентом).

На рис. 4(а) показан график функции 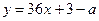для значений параметра а, взятых из выше приведенной таблицы.

По поводу этого графика можно сказать следующее:

1. При конкретном значении a график функции 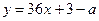является прямой с угловым коэффициентом 36, пересекающей ось y в точке с ординатой 3 – a (см. рис. 4(б)).

2. С увеличением значения параметра a прямая 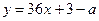смещается параллельно вниз, с уменьшением значения параметра a эта прямая смещается параллельно вверх.

На рис. 5 видно, что прямая 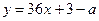имеет с графиком функции 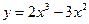ровно две общие точки только в том случае, если касается этого графика в одной из этих точек и пересекает его в другой.

Поэтому задача фактически сводится к тому, чтобы узнать значения параметра а, при каждом из которых прямая 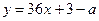является касательной к графику функции .

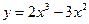Пусть x и y – координаты точки касания прямой с графиком функции 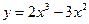. Найдем значения x, y и a из системы уравнений:

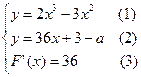Уравнения (1) и (2) системы означают, что точка касания принадлежит обоим графикам, то есть является их общей точкой. А вот уравнение (3) выражает геометрический смысл производной:

производная функции в некоторой точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Итак, начинаем решение системы с уравнения (3):

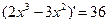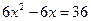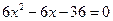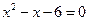Корнями данного квадратного уравнения являются числа:

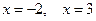Подставляя 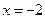в уравнение (1), получим:

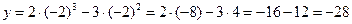Таким образом, мы нашли первую точку касания: T (– 2; – 28). Подставляя далее ее координаты в уравнение (2), находим значение параметра a:

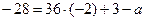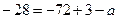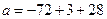
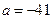Подставляя в уравнение (1) 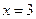и действуя аналогичным образом, можно найти координаты второй точки касания, а также значение параметра 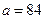. Проделайте соответствующие выкладки самостоятельно. Разумеется, найденные ответы a = – 41 и а = 84 совпали с теми, которые были получены в предыдущем пункте.

Исследование количество решений уравнения с параметром.
Общий случай.

Решим следующую задачу.

Задача 2. Определите, сколько корней в зависимости от значения параметра a имеет уравнение

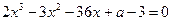Решение.

Прежде всего, обратим внимание на то, что эта задача по своему условию соответствует уже разобранной нами ранее задаче 1, только вопрос на этот раз ставится в более общей форме. Поэтому будем решать задачу 2 так же, как и задачу 1.

Перепишем уравнение в виде

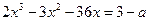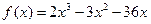
Введем две функции:

Тогда исходное уравнение можно переписать в виде

f(x) = g(x)

и переформулировать задачу в равносильной форме:

определите, сколько общих точек в зависимости от значения параметра a имеют графики функций f(x) и g(x).

Эскиз графика функции изображен на рис. 6. По поводу графика функции y = 3 – a мы уже высказывались ранее, но будет совсем не лишним повторить эту информацию:

1. При конкретном значении a график функции y = 3 – a является горизонтальной прямой, пересекающей ось y в точке с ординатой 3 – a (см. рис. 2 (б)).

2. С увеличением значения параметра a прямая y = 3 – a смещается параллельно вниз, с уменьшением значения параметра a эта прямая смещается параллельно вверх (см. рис. 2 (а)).

Из всевозможных расположений прямой y = 3 – a можно выделить всего пять (см. рис. 6):

( I) и ( V) – в этих положениях прямая и график функции имеют одну общую точку;

( II) и ( IV) – в этих положениях прямая и график функции имеют две общие точки;

( III) – в этом положении прямая и график функции имеют три общие точки.

Заметим, что значения параметра a, соответствующие положениям ( II) и ( IV), нами уже были найдены при решении задачи 1: значение a = – 41 соответствует положению ( II), значение a = 84 соответствует положению ( IV).

Теперь нетрудно определить значения параметра a для других расположений прямой, если применить свойства графика функции y = 3 – a, о которых мы упомянули выше.

Чтобы попасть в положение ( I), надо сместить прямую y = 3 – a из положения ( II) параллельно вверх. Тогда значение параметра a уменьшится. Так как в положение ( II) значение параметра было равно a = – 41, то в положение ( I) оно будет удовлетворять условию .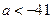

Чтобы попасть в положение ( V), надо сместить прямую y = 3 – a из положения ( IV) параллельно вниз. Тогда значение параметра a увеличится. Так как в положение ( IV) значение параметра было равно a = 84, то в положение ( V) оно будет удовлетворять условию .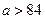

В обоих случаях мы воспользовались свойством:

с увеличением значения параметра a прямая y = 3 – a смещается параллельно вниз, с уменьшением значения параметра a эта прямая смещается параллельно вверх.

Давайте для определения значений параметра a в положение ( III) воспользуемся другим свойством:

прямая y = 3 – a пересекает ось y в точке с ординатой, равной 3 – a.

Итак, в положение ( II) прямая пересекает ось y в точке с ординатой 44, а в положение ( IV) – в точке с ординатой – 81. Значит, в положение ( III) ордината точки пересечения прямой с осью y, равная 3 – a, должна колебаться между числами – 81 и 44, то есть удовлетворять условию

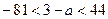Решая это двойное неравенство, получаем

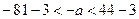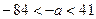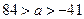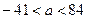И, наконец, вспомнив, что количество общих точек графиков y = 3 – a и равно числу корней исходного уравнения с параметром, напишем ответ к задаче.

Ответ: уравнение имеет один корень при 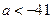, 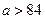; два корня при a = – 41, а = 84; три корня при .

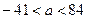Особые расположения графика с параметром при
исследовании параметрического уравнения.

Обратите внимание, что при решении задачи 2 ключевым вопросом является информация о том, при каких значениях параметра a прямая y = 3 – a занимает положения ( II) и ( IV). Эти расположения графика с параметром я называю особыми. Любую задачу на нахождение числа решений уравнения в зависимости от значений параметра нужно начинать именно с исследования таких положений.

Особое положение графика с параметром удовлетворяет следующим условиям:

1) оно фиксировано; 2) при малейшем отклонении от этого положения хотя бы в одну сторону изменяется число общих точек пересечения графика с параметром и обычного графика, то есть изменяется число решений уравнения с параметром.

Так положение ( II) прямой y = 3 – a (см. рис. 6) особое по следующим причинам:

1) оно фиксировано (прямая проходит через точку А); 2) малейшее отклонение прямой от этого положения приводит к изменению количества общих точек этой прямой и графика функции . Если прямая отклоняется немного вверх, количество общих точек уменьшается до одной. Если же прямая отклоняется от положения ( II) немного вниз, то количество общих точек увеличивается до трех.

Дата добавления: 2022-11-11; просмотров: 36; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!