Степени подвижности и класс механизма
Манипулятором называется техническое устройство, предназначенное для воспроизведения рабочих функций руки человека. Первые конструкции манипуляторов не только по назначению, но и по внешнему виду напоминали руку человека.
В задачу структурного анализа пространственных механизмов (манипуляторов)
входит определение числа степеней свободы и маневренности манипулятора. Манипуляторы как исполнительные устройства промышленных роботов представляют собой пространственные механизмы различных структурных схем с несколькими степенями подвижности, выполняемые в виде незамкнутых кинематических цепей.
Обычно манипулятор имеет шесть или большее число степеней свободы (подвижности), из которых три используются для перемещения (переноса) объекта из одной точки пространства в другую по заданной траектории с регламентированным законом движения; три других обеспечивают требуемую ориентацию объекта в пространстве [4].
В роботе-манипуляторе Dobot Magikian имеется 5 степеней свободы, что является 4 классом механизма.
Движение по осям:
§ Диапазон / Макс. скорость (при нагрузке 250 г.)
§ Соединение 1 база: от –135° до +135° / 320°
§ Соединение 2 задний рычаг: от –0° до +85° / 320°
§ Соединение 3 передний рычаг: от –10° до +95° / 320°
§ Соединение 4 поворотный серводвигатель: от +90° до –90° / 480°
Кинематическая схема манипулятора
Полное математическое описание должно состоять из трех моделей:
|
|
|
1. Кинематической, отображающей кинематическую структуру манипулятора.
2. Динамической, описывающей динамическую структуру, необходимую для реализации и оценки динамических уравнений.
3. Электромеханической, описывающую связь механической и электрической частей манипулятора.
Кинематическая схема пятизвенного манипулятора Dobot Magician представленна на рисунке 3.
Кинематическая модель робота была составлена с помощью представления Денавита-Хартенберга, так же была составлена кинематическая модель робота и произведено моделирование работы в программном комплексе MATLAB.
Рабочая область манипулятора приведена на рисунке 2:
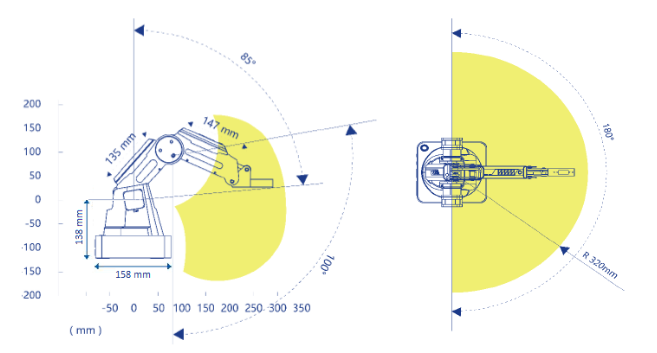
Рисунок 2. Рабочая часть манипулятора.
РЕШНИЕ ПРЯМОЙ И ОБРАТНОЙ ЗАДАЧИ КИНЕМАТИКИ
Кинематический анализ манипулятора включает в себя решение прямой и обратной задача кинематики. За счет решения этих задач определяется взаимосвязь между координатами в пространстве.
Dobot Magician состоит из пяти звеньев, связанных между собой вращательными и поступательными сочленениями. На рисунке 3 изображена нулевая конфигурация, то есть положение, при котором все обобщенные координаты равны нулю и размеры каждого звена, приведенные в мм.
|
|
|
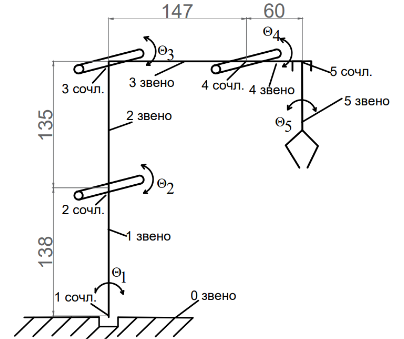
Рисунок 3. Схема кинематическая пятизвенного манипулятора Dobot Magician.
Прямая задача кинематики
Использование метода Денавита-Хартенберга позволяет сократить число координат, определяющих положение и ориентацию твердого тела в пространстве, с шести до четырех [2].
Метод Денавита-Хартенберга состоит из нескольких этапов:
1. На первом этапе необходимо привязать системы координат к звеньям.
2. Определение параметров Денавита-Хартенберга.
3. Построение матриц однородного преобразования.
Для привязки системы координат к звеньям необходимо учитывать несколько правил:
· Выбор осей zi – необходимо выбрать ось 𝑧𝑖 так, чтобы она совпала с осью вращения или поступательного движения последующего сочленения 𝑖 + 1.
· Выбор осей xi – необходимо выбрать ось xi так, чтобы она пересекала и была перпендикулярна оси zi-1.
· Выбор осей yi – необходимо выбрать ось yi так, чтобы она дополняла систему координат до правой [2].
Выбранные системы координат каждого звена представлены на рисунке 4.
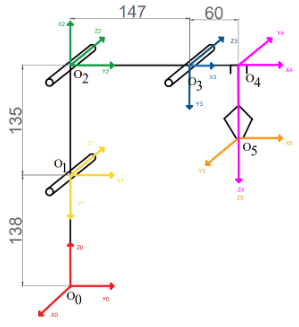
Рисунок 4. Выбор системы координат манипулятора.
Четыре параметра Денавита-Хартенберга вычисляются следующим образом:
· 𝑎𝑖 — расстояние между Oi-1 и Oi вдоль оси Xi;
|
|
|
· 𝛼𝑖 — угол, на который необходимо повернуть Zi-1 вокруг Xi, чтобы она стала сонаправлена с Zi;
· 𝑑𝑖 — расстояние между Oi-1 и Oi вдоль оси Zi-1;
· 𝜃𝑖 — угол поворота оси Xi-1 вокруг оси Zi-1, чтобы она стала сонаправлена с осью Xi [2].
Таблица 1. Параметры Денавита-Хартенберга манипулятора.
| Звено i | 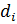 , м , м
| 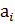 , м , м
| 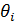 , ° , °
| 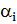 ,° ,°
|
| 1 | 0,138 | 0 | 90 | -90 |
| 2 | 0 | 0,135 | -90 | 0 |
| 3 | 0 | 0,147 | 90 | 0 |
| 4 | 0 | 0,06 | 0 | -90 |
| 5 | 0,01 | 0 | 0 | 0 |
По полученным четырем параметрам для каждого звена манипулятора построим матрицу однородного преобразования от основания к рабочему органу в общем виде.
ú
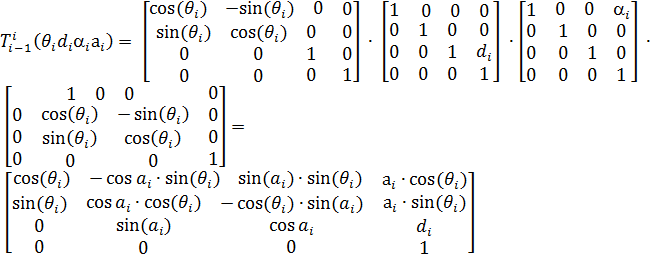 (1)
(1)
Подставив все параметры Денавита-Хартенберга, получим 𝑛 матриц однородного преобразования (1):
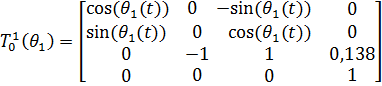 (2)
(2)
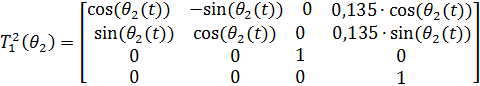 (3)
(3)
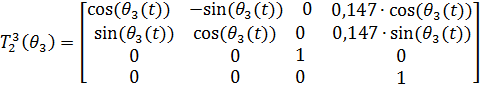 (4)
(4)
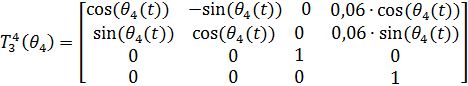 (5)
(5)
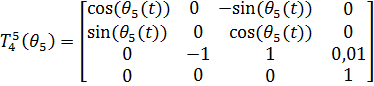 (6)
(6)
Итоговую матрицу, связывающую все полученные системы координат, можно получить путем перемножения всех полученных ранее матриц однородного преобразования (2-6):
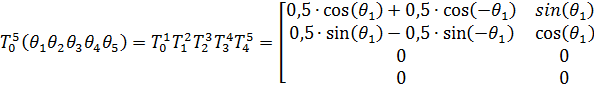
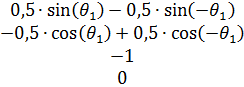
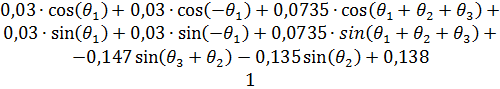
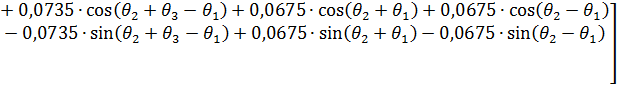 (7)
(7)
Итоговая матрица однородного преобразования характеризует связь трех систем координат.
Обратная задача кинематики
Геометрический (аналитический) метод решения обратной задачи кинематики заключается в нахождении в явном виде выражений при использовании тригонометрических функций, учитывая кинематические схемы манипулятора. Используя зависимости координат от присоединенных переменных, выведенные из однородной матрицы преобразований, найдём присоединенные переменные [3]:
|
|
|
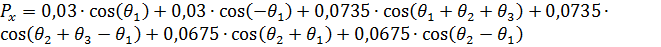 (8)
(8)
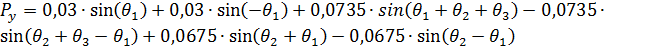 (9)
(9)
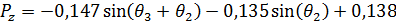 (10)
(10)
Упростим выражения (8), (9), (10):
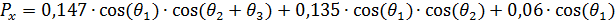 (11)
(11)
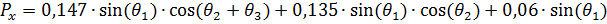 (12)
(12)
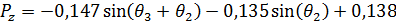 (13)
(13)
Вычисление 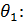
Вычтем (12) из (11), затем(11) 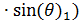 , (12)
, (12) 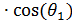
Вся правая часть уравнения сокращается:
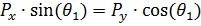 (14)
(14)
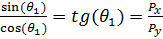 (15)
(15)
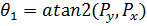 (16)
(16)
Вычисление 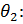
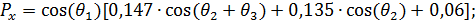 (17)
(17)
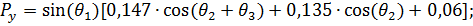 (18)
(18)
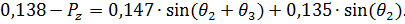 (19)
(19)
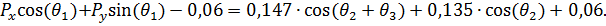 (20)
(20)
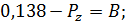 (21)
(21)
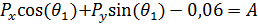 (22)
(22)
Возведём (19) и (20) в квадрат и сложим:
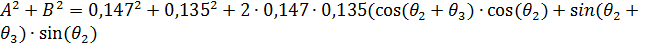 (23)
(23)
Произведя сокращения получаем:
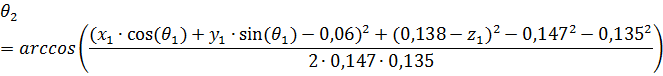
(24)
Вычисление 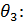
Разделим (11) 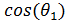 , а (13) на
, а (13) на 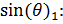
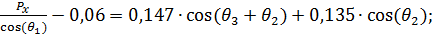 (25)
(25)
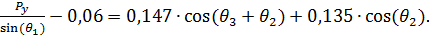 (26)
(26)
Возведем (25) и (19) в квадрат и сложим их. Произведя сокращения, получаем:
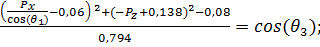 (27)
(27)
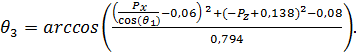 (28)
(28)
Из выражений (11), (12), (13) получаем уравнения неизвестных углов:
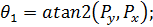 (29)
(29)
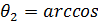
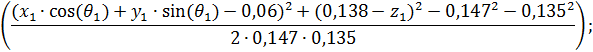
(30)
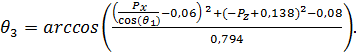 (31)
(31)
Подставив вычисленные уравнения углов (16), (24), (28) в уравнения присоединенных переменных (8-10), получим координаты рабочего органа манипулятора в м:
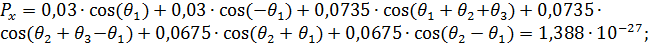 (32)
(32)
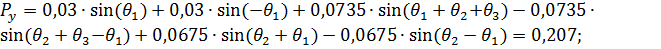 (33)
(33)
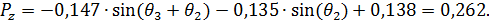 (34)
(34)
Результаты, полученные в виде уравнений углов, с помощью которых вычисляется положение рабочего органа, можно сравнить с фактическим измерением заданного положения рабочего органа манипулятора по таблице 2.
Таблица 2. Сравнение результатов.
| Расчетные значения | |
| Вычисленные уравнения для углов | Координаты положения рабочего органа (x, y, z), м |
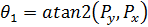
| 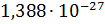
|
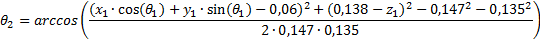
| 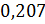
|
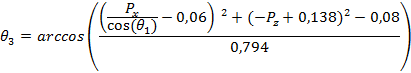
| 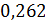
|
Продолжение таблицы 2. Сравнение результатов.
| Измененные значения | |
| Заданные углы, º | Координаты положения рабочего органа (x, y, z), м |
| 90 | 0 |
| - 90 | 0,21 |
| 90 | 0,27 |
Дата добавления: 2022-11-11; просмотров: 161; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
