К вычислению значений числа степеней свободы

Принципиально числа степеней свободы вычисляются в соответствии с общепринятыми представлениями.

4. Определяем числа степеней свободы.

4.1. Общее число степеней свободы (для общей дисперсии):

4.2. Число степеней свободы по фактору А (для дисперсии по фактору А):

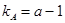4.3. Число степеней свободы по фактору В (для дисперсии по фактору В):

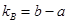4.4. Число степеней свободы по фактору С (для дисперсии по фактору С):

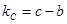4.5. Число степеней свободы по случайным факторам (для остаточной дисперсии), оно вычисляется как разность значений общей численности дисперсионного комплекса (общее число наблюдений) и числа градаций фактора низшей иерархии (в нашем примере число учетных побегов):

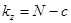К вычислению средних квадратов отклонений или дисперсий

5. Находим средние квадраты отклонений по факторам, используя полученные величины соответствующих сумм квадратов отклонений и числа степеней свободы.

5.1. По фактору А – фактору высшего уровня иерархии:

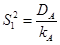5.2. По фактору В – фактору промежуточного уровня иерархии:

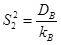5.3. По фактору С – фактору низшего уровня иерархии:

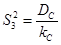5.3. По остаточной вариации – по случайным факторам – Z:

5.4. Результат записываем в таблицу (табл. 2):

Таблица 2.

Результаты дисперсионного анализа массы хвои плюсовых деревьев сосны обыкновенной в составе лесосеменной плантации № 24

Вариация	Степени свободы (k)	Суммы квад-ратов (D)	Средние квад-раты (S)	Дисперсионные отношения
				F _факт	F _ст
				F _факт	5%	1%
1	2	3	4	5	6	7
По фактору А	k_A			F_A = S² _А /S² _В =
По фактору В	k_B			F_B = S² _В /S² _С =
По фактору С	k_C			F _С = S² _С /S²_Z =
Остаточная	k_z			-	-	-
Общая	k_y			-	-	-

Статистически доказанным оказалось влияние фактора А.

Для получения исправленных значений дисперсий, используемых в расчетах по методу Снедекора, в неравномерных комплексах необходимо вычислить усредненные значения численностей по каждому организованному фактору.

К расчету усредненных численностей групп дисперсионного комплекса

Мы с вами уже знаем, что усредненные численности групп используются в расчетах исправленных значений дисперсий организованных факторов при вычислении коэффициента наследуемости (эффективности действия фактора) по методу Снедекора в неравномерных дисперсионных комплексах.

В трехфакторном анализе учитывают величины дисперсий, вызванных отдельным действием каждого из факторов, имеющих иерархическую соподчиненность. Эффект взаимодействия факторов в иерархических комплексах не вычисляют.

В соответствии с этим вычисляют:

- дисперсию по фактору А – различия между плюсовыми деревьями (ортетами);

- дисперсию по фактору В – различия между учетными деревьями одного плюсового дерева (раметами);

- дисперсию по фактору С – различия между учетными побегами одного учетного дерева.

В вычислениях используют усредненные численности групп соответствующих иерархий (иерархических уровней):

- усредненное число наблюдений в пределах одного плюсового дерева (численность всех учетов на всех раметах одного плюсового дерева) для расчета по фактору А;

- усредненное число наблюдений в пределах одного учетного дерева (численность всех учетов на всех побегах одного учетного дерева) для расчета по фактору В;

- усредненное число наблюдений в пределах одного учетного побега (численность всех учетов на одном учетном побеге) для расчета по фактору С.

6.1. Усредненное значение численности градаций фактора высшей иерархии (градации фактора А) неравномерного иерархического комплекса для расчета дисперсии по первому фактору – фактору А (усредненное значение численности одной градации высшего – первого – порядка):

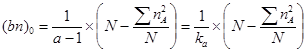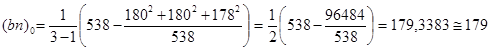
6.2. Усредненное значение численности градаций фактора промежуточной иерархии (градации фактора В) неравномерного иерархического комплекса для расчета дисперсии по второму фактору – фактору В (усредненное значение численности одной градации промежуточного – второго – порядка):

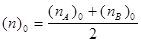, где

6.3. Усредненное значение числа наблюдений в градациях фактора В по градациям фактора А – коррекция неравномерности градаций фактора высшей иерархи (а - 1 – адекватно числу степеней свободы по фактору А). Примечание: в учебнике Г.Ф. Лакина (1980, стр. 251) приведена некорректная запись алгоритма вычислений. Представленная в настоящем виде формула корректна (Бессчетнов В.П.):

;

Усредненная численность группы (комплекса столбцов, принадлежащих одному учетному дереву – усредненная численность одной градации фактора В) с поправкой на неравномерность численностей групп по плюсовым деревьям – учитывает как неодинаковое число учетных деревьев в каждом плюсовом дереве (в составе клонов одного плюсового дерева), так и неодинаковую численность учетов (дат) в каждом частном столбце, относящемся к одному плюсовому дереву.

- nb – численность одной градации фактора В (численность учетов в одной рамете);

- Σnb ² _iA – сумма квадратов численностей одной градации фактора В (численность учетов в одной рамете) в пределах одной градации фактора А;

- Σnb ² _i – общая сума квадратов численностей градаций фактора В по всему дисперсионному комплексу;

- n_A – численность соответствующей градации фактора А (число учетов в отдельной градации фактора А – в одном ортете);

- N – общая численность дисперсионного комплекса;

- k_a – число степеней свободы фактора А.

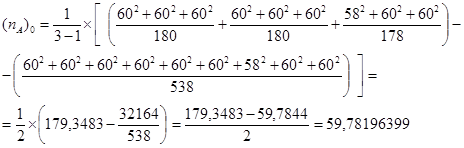
6.4. Усредненное значение числа наблюдений в градациях по фактору В (b – a – адекватно числу степеней свободы по фактору В) – коррекция неравномерности градаций фактора промежуточной иерерхии. Примечание: в учебнике Г.Ф. Лакина (1980, стр. 251) приведена некорректная запись алгоритма вычислений. Представленная в настоящем виде формула корректна (Бессчетнов В.П.):

Усредненная численность группы (комплекса столбцов, принадлежащих одному учетному дереву – усредненная численность одной градации фактора В) с поправкой на неравномерность численностей групп по учетным деревьям – учитывает как неодинаковое число учетных деревьев в каждом плюсовом дереве (в составе клонов одного плюсового дерева), так и неодинаковую численность учетов (дат) в каждом частном столбце, относящемся к одному плюсовому дереву.

6.5. После чего:

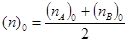Общая усредненная численность отдельной градации фактора В (усредненное общее число учетов по всей группе столбцов, принадлежащих одному учетному дереву) с поправкой на неравномерность численностей групп по плюсовым деревьям. Здесь:

- ( n )₀ – общая усредненная численность одной полной градации фактора промежуточной иерархии В (среднее число учетов – дат – в одной градации фактора В) для всего дисперсионного комплекса с учетом неравномерности общих численностей градаций фактора А.

- ( n _А )₀ – усредненная общая численность группы (комплекса столбцов, принадлежащих одному учетному дереву) с поправкой на неравномерность численностей групп по плюсовым деревьям – по фактору А;

- ( n _В )₀ – усредненная численность группы (комплекса столбцов, принадлежащих одному учетному дереву) с поправкой на неравномерность численностей групп по учетным деревьям – по фактору В;

6.5. Усредненное значение численности градаций фактора низшей иерархии (градации фактора С) неравномерного иерархического комплекса для расчета дисперсии по третьему фактору – фактору С (усредненное значение численности одной градации низшего – третьего – порядка):

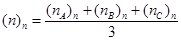, где

6.6. Усредненное значение числа наблюдений в градациях фактора С с поправкой на неравномерность фактора А

, где:

- n с _iA – численность одной градации фактора низшей иерархии С в пределах одной градации фактора высшей иерархии А (численность частных учетов в одном ортете);

- Σn с² _iA – сумма квадратов численностей столбцов в одной градации фактора А (численность учетов в каждой из градаций фактора низшей иерархии С в одном ортете) в пределах одной градации фактора А;

- Σn а² _i – общая сума квадратов численностей градаций фактора А по всему дисперсионному комплексу;

- n_Ai – численность соответствующей градации фактора А (число учетов в отдельной градации фактора А – в одном конкретном ортете);

- N – общая численность дисперсионного комплекса;

- a – число градаций фактора А;

- k_a – число степеней свободы фактора А.

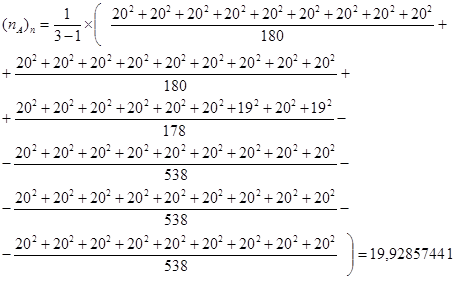
6.7. Усредненное значение числа наблюдений в градациях фактора С с поправкой на неравномерность фактора В:

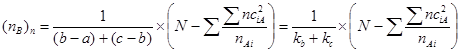, где:

- Σn са² _i / n_Ai – усредненное значение численностей градации фактора низшей иерархии С в пределах одной градации фактора А;

- N – общая численность дисперсионного комплекса;

- a – число градаций фактора А;

- b – число градаций фактора В;

- с – число градаций фактора С;

- k_b – число степеней свободы фактора B;

- k_c – число степеней свободы фактора C.

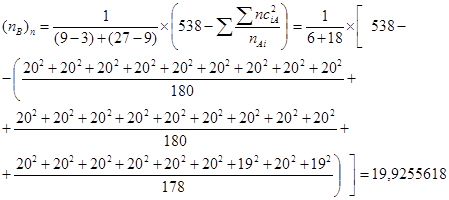
6.8. Усредненное значение числа наблюдений в градациях фактора С с поправкой на неравномерность градаций фактора С

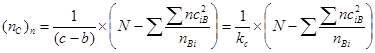, где:

- n с _i _В – численность одной градации фактора низшей иерархии С в пределах одной градации фактора промежуточной иерархии В (численность частных учетов в одной рамете);

- Σn с² _i _В – сумма квадратов численностей столбцов в одной градации фактора В (численность учетов в каждой из градаций фактора низшей иерархии С в одной рамете) в пределах одной градации фактора В;

- Σn с² _i _В / n _В _i – усредненное значение численностей градации фактора низшей иерархии С в пределах одной градации фактора В;

- n _В _i – численность соответствующей градации фактора В (число учетов в отдельной градации фактора В – в одной конкретной рамете);

- N – общая численность дисперсионного комплекса;

- b – число градаций фактора В;

- с – число градаций фактора С;

- k_c – число степеней свободы фактора C.

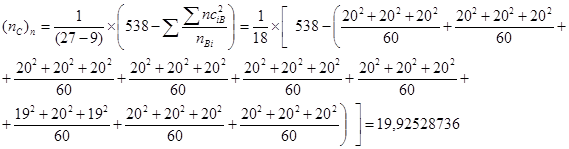
6.5. После чего:

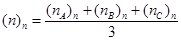, где

- ( n ) _n – общая усредненная численность одной градации фактора низшей иерархии С для всего дисперсионного комплекса с учетом неравномерностей всех организованных факторов.

- ( n _А ) _n – усредненная численность одной градации фактора низшей иерархии С с учетом поправки на неравномерность градаций фактора высшей иерархии А;

- ( n _В ) _n – усредненная численность одной градации фактора низшей иерархии С с учетом поправки на неравномерность градаций фактора промежуточной иерархии В;

- ( n _С ) _n – усредненная численность одной градации фактора низшей иерархии С с учетом поправки на неравномерность численности градаций фактора низшей иерархии С.

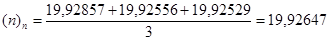
7. На следующем этапе рассчитываем факториальные и общую дисперсии.

7.1. Дисперсия по фактору А:

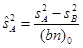7.2. Дисперсия по фактору В:

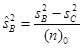7.3. Дисперсия по фактору С:

7.3. Общая дисперсия:

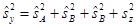8. Далее рассчитываем силу влияния факторов.

8.1. Сила влияния фактора А (эффект влияния ортетов):

8.2. Сила влияния фактора В, включая совместное влияние АВ (эффект влияния рамет совместно с эффектом взаимодействия компонентов дисперсии ортетов и рамет):

8.2. Сила влияния фактора С, включая совместное влияние ВС (эффект влияния рамет совместно с эффектом взаимодействия компонентов дисперсии рамет и учетных побегов):

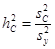8.3. Сила влияния неорганизованных факторов

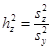8.4. Проверяем правильность расчета показателей силы влияния факторов, исходя из того, что сумма оценок доли влияния каждого из факторов должна быть равна «единице»:

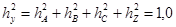Дата добавления: 2022-11-11; просмотров: 40; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!