НЕПРЕРЫВНОСТЬ ФУНКЦИИ. ТОЧКИ РАЗРЫВА.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
1. Функции, пределы, бесконечно большие, бесконечно малые.
Рассмотрим два множества X и Y, элементами которых могут быть любые объекты. Допустим, что каждому элементу х множества Х по некоторому закону поставлен в соответствие не более одного элемента множества У, который обозначим у = f (х). Тогда f называют функцией из Х в У (или отображением множества X в Y ).
х – область определения функции.
f ( X ) – множество значений функции. f (х) – это часть (или все) множества Y.
х – независимая переменная – аргумент.
Равенство у = f (х) означает, что применив к аргументу х закон f, найдем соответствующее этому х значение у.
Способы задания функции: словесный, табличный, аналитический (формулой), графический.
Основные элементарные функции:
1) Степенная функция у = хα, где 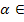 R ( R – множество действительных чисел).
R ( R – множество действительных чисел).
2) Показательная функция у = ах, где а>0, а≠1.
3) Логарифмическая функция у = 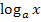 , где а>0; а≠1.
, где а>0; а≠1.
4) Тригонометрические функции y = 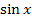 ; y =
; y =  ; y = tg x ; y = ctg х.
; y = tg x ; y = ctg х.
5) Обратные тригонометрические функции у = arcsin x ; у = arcos x ; у = arctg x ; у = arcctg x.
Некоторые классы элементарных функций:
1) Целая рациональная функция (многочлен)
у = а0х n + а1х n -1 + а2 х n -2 + … + а n -1 х + а n,
где n – целое неотрицательное число (степень многочлена);
а0; а1; а2; … а n – постоянные числа (коэффициенты).
2) Дробно–рациональная функция – отношение двух целых рациональных функций:
|
|
|
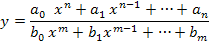
Пусть функция f(x) определена на множестве N ={1, 2, 3,… n …}- всех натуральных чисел.
Её называют бесконечной числовой последовательностью.
Обозначим f ( n )= xn, тогда последовательность можно записать так:
{ xn }= x 1 ; х2; х3…х n… .
Последовательность считается заданной, если известен закон ее образования, т.е. правило, по которому можно определить любой член последовательности.
Число а называют пределом членовой последовательности {xn}, если для любого  , существует такой
, существует такой 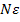 , начиная с которо
, начиная с которо 
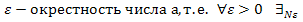 :
: 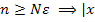 n - a |
n - a | 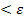 .
.
Интервал (а - 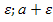 ) называют
) называют 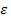 окрестностью точки а.
окрестностью точки а.

х n 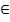 (
( 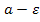 ; a +
; a +  )
)  |х n – а| <
|х n – а| < 
Символическая запись: 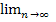 х n = a (х n → a, т.е. х n сходится к а).
х n = a (х n → a, т.е. х n сходится к а).
{xn} - называют сходящейся последовательностью, если она имеет предел.
{xn} - расходящаяся, если нет предела, т.е. 
Примеры:
1) xn = 
{xn}: 1;  ;
;  ;
;  ;
;  …
…  ….
….
при n → ∞  → 0, т.е.
→ 0, т.е. 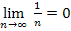
2) xn = 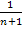
{xn}:  ;
;  ;
;  ;
;  ;
;  …
… 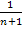 ….
….
при n → ∞  → 1, т.е
→ 1, т.е  .
.
3) xn = n 2
{xn}: 1; 4; 9; 16 … n 2…
при n → ∞ n 2 → ∞ 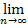 n 2 = ∞ - нет предела.
n 2 = ∞ - нет предела.
Если предел последовательности {xn} равен 0, то её называют бесконечно малой, если ∞, то бесконечно большой
|
|
|
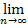 xn = 0
xn = 0 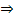 {xn} – бесконечно малом
{xn} – бесконечно малом
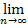 xn = ∞
xn = ∞ 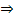 {xn} – бесконечно большом.
{xn} – бесконечно большом.
Если {xn} – бесконечно малом, то 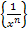 – бесконечно большая и наоборот.
– бесконечно большая и наоборот.
Теоремы о пределах.
Если 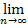 а n = a ;
а n = a ; 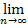 bn = b, то
bn = b, то
1) 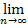 (an
(an 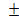 bn) =
bn) = 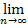 an ±
an ± 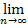 bn = a+b
bn = a+b
2) 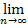 (an
(an  bn) =
bn) = 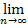 an
an 
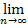 bn = ab
bn = ab
3) 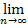 kan = k
kan = k 
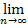 an = ka (k-число)
an = ka (k-число)
4) 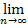
 =
= 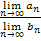 =
= 
Примеры:
1) 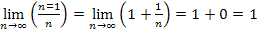
2) 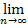
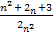 =
= 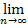
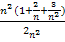 =
= 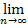
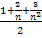 =
= 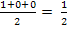
3) 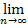
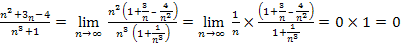
4) 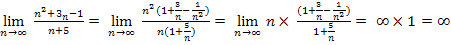 - нет предела
- нет предела
Число А называется пределом функции f ( x )
x → a, если для любого числа ε > 0 можно указать такое число δ > 0, что для любого х ≠ а удовлетворяющего неравенству |х – а| < δ выполняется неравенство |f ( x ) – А|< ε
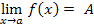
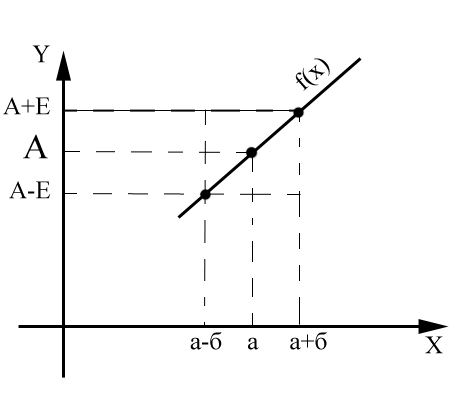
Если А1 является пределом функции f ( x ) в точке a, х 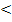 а, то А1 – предел функции слева, и обозначается
а, то А1 – предел функции слева, и обозначается 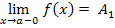
Если А2 является пределом функции f ( x ) в точке а и х>а, то А2 – предел функции справа и обозначается 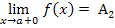
А1; А2 – односторонние пределы.
Если  , то f ( x ) – бесконечно малая при х→а.
, то f ( x ) – бесконечно малая при х→а.
Если 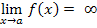 , то f ( x )- бесконечно большая при х→а.
, то f ( x )- бесконечно большая при х→а.
Если f ( x ) – бесконечно малая, то 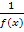 - бесконечно большая и наоборот.
- бесконечно большая и наоборот.
Теоремы о пределах:
Если существуют пределы функций f ( x ) и φ(х) при х→а, то
1) 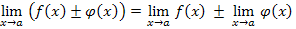
2) 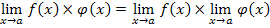
3)  ; если
; если 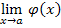 ≠0
≠0
4) Если f ( x ) – элементарная функция, то
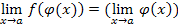
Например:  =
= 
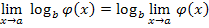
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
|
|
|
Следствия:
1) 
2) n 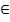 N
N  ;
; 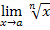 =
= 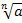
3) Предел многочлена
P ( x ) = a 0 xn + a 1 xn -1 +…+ an при x → a 
4) Предел дробно-рациональной функции
R ( x ) = 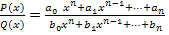 при х→а равен значению этой функции при х= Q, если а принадлежит области определения функции
при х→а равен значению этой функции при х= Q, если а принадлежит области определения функции 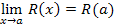 .
.
Замечательные пределы:
1) 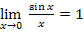
2) 
При вычислении пределов функции используем следующее:
1) Если функции f ( x ) определена в предельной точке х=а, то 
Примеры:
а) А= 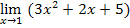 -
-
воспользуемся теоремами о пределах:
А= 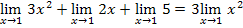 +2
+2 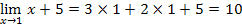
б) B= 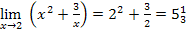
2) Если функция f ( x ) не определена в предельной точке, то имеет место неопределенность.
Она может иметь вид 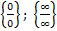
Элементарные приемы раскрытия неопределенностей:
а) сокращение на множитель, создающий неопределенность;
б) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при х→∞);
в) применение эквивалентных бесконечно малых;
г) использование замечательных пределов и следующих свойств:
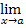
 , если
, если  , т.е.
, т.е. 
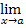
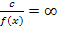 , если
, если 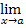 f ( x )=0, т.е.
f ( x )=0, т.е. 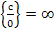
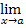
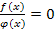 , если
, если 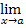 f ( x )
f ( x ) 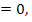 а
а 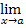
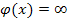 , т.е.
, т.е. 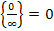
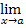
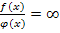 , если
, если 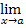 f ( x )
f ( x )  ; а
; а 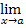
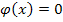 , т.е.
, т.е. 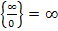
Примеры:
а) А= 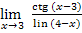
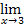 ctg (x-3)=∞;
ctg (x-3)=∞; 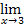 ln(4-х)=0 А=∞;
ln(4-х)=0 А=∞;
б) А= 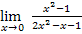 так как
так как 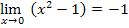 существует и конечен,
существует и конечен,
|
|
|
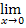 (
(  , существует, конечен и не равен 0, то
, существует, конечен и не равен 0, то
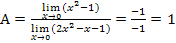
в) А=  при подстановке предельного значения имеем
при подстановке предельного значения имеем 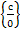 , значит А=∞;
, значит А=∞;
г) А= 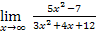 Имеем неопределенность вида
Имеем неопределенность вида 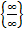 .
.
Делим числитель и знаменатель на старшую степень х на х2.
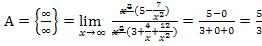
При  являются бесконечно малыми;
являются бесконечно малыми;
д) 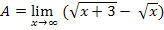 Имеем неопределенность вида {∞ - ∞}.
Имеем неопределенность вида {∞ - ∞}.
До множим и разделим на сокращенное выражение

е) 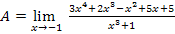 Имеем неопределенность вида
Имеем неопределенность вида 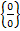 , так как многочлен в числителе и знаменателе имеют корень -1. Надо сократить дробь на критический множитель x+1:
, так как многочлен в числителе и знаменателе имеют корень -1. Надо сократить дробь на критический множитель x+1:
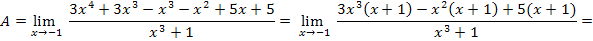
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 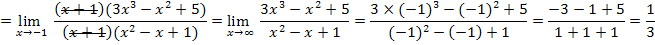
ж) 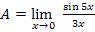 Имеем неопределенность вида
Имеем неопределенность вида 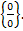
Раскроем её при помощи первого замечательного предела.
Аргумент синуса и знаменатель должны совпадать, поэтому до множим числитель и знаменатель на 5, чтобы получить  .
.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ. ТОЧКИ РАЗРЫВА.
Пусть функции f ( x ) определена на некотором множестве и а - предельная точка из этого множества.
Функция f(x) называется непрерывной в точке а, если:
1) Она определена в точке а
2) Существует конечный предел 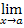 f ( x )
f ( x )
3) Этот предел равен значению функции в точке a
Или: 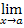 f ( x ) = f ( a ) – это условие непрерывности
f ( x ) = f ( a ) – это условие непрерывности
Если условие непрерывности в точке а нарушено, то такую точку называют точкой разрыва, и говорят, что функция терпит разрыв в точке а.
Все элементарные функции непрерывны на своей области определения и могут иметь разрыв только в точках, в которых не определены.
Пусть функция f ( x ) имеет разрыв в точке a.
Если существуют конечные пределы справа и слева
A1 = 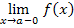 и А1 =
и А1 = 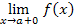 , то имеет место разрыв I рода.
, то имеет место разрыв I рода.
Если хотя бы один из односторонних пределов не существует, т.е
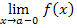 = ∞ или
= ∞ или 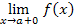 =∞ то имеет место разрыв II рода.
=∞ то имеет место разрыв II рода.
АСИМПТОТЫ.
Прямая y = ƙ x + в называется асимптотой кривой y = 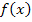 , если расстояние от точки
, если расстояние от точки
P ( x ; f ( x )), лежащей на кривой, до этой прямой стремиться к нулю при х → +∞ ( x → -∞).
Бывают:
1. Вертикальные
График функции f ( x ) имеет вертикальную асимптоту x = a, если при x → a  = ∞ или
= ∞ или  = -∞
= -∞
2. Горизонтальные
График функции y = f ( x ) имеет горизонтальную асимптоту
y = b, если 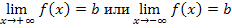
3. Наклонные
Если для функции f ( x ) можно найти конечные пределы 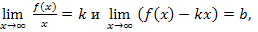
то график этой функции имеет наклонную асимптоту y = kx + b.
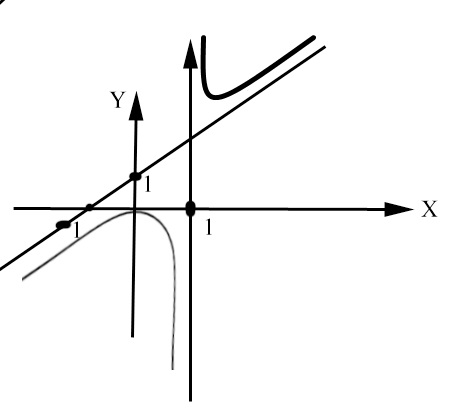
Пример:
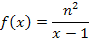
а) х=1 – точка, в которой функция не определена 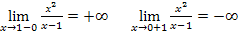
x=1 – вертикальная асимптота;
б) 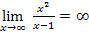 - нет предела
- нет предела  нет горизонтальных асимптот;
нет горизонтальных асимптот;
в)  k = 1
k = 1
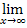 (
( 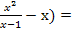
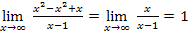 , то есть b =1
, то есть b =1
y = x+1 – наклонная асимптота.
ПРОИЗВОДНАЯ ФУНКЦИЯ.
Производной функцией в точке х0 называется предел отношения приращения функции 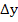 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента  , при условии, что
, при условии, что  , то есть
, то есть

Дата добавления: 2022-11-11; просмотров: 84; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
