Основные правила комбинаторики
Методы решения
Комбинаторных задач
Перебор вариантов
Основные правила комбинаторики
Формулы для подсчета числа перестановок,
Сочетаний и размещений
Специальные приемы, используемые
При решении комбинаторных задач
Введение
Комбинаторика изучает способы подсчета числа элементов множества. Она формулирует правила подсчета для некоторых множеств. Комбинаторные методы применяются в теории вероятностей, статистике, экономике, теории игр, физике, химии, биологии и многих других областях науки, техники и производства.
Задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций получили название комбинаторных задач.
Перебор вариантов
Перебор вариантов используется при решении так называемых перечислительных задач. Данный метод занимает центральное место в элементарной комбинаторике. Он используется в случае, когда число всех возможных вариантов построения комбинаций не велико.
Перебор вариантов можно осуществлять различными способами:
- непосредственно перебирая все возможные случаи;
- изображая графы;
- используя дерево возможных вариантов;
- составляя таблицы.
При этом следует понимать, что перечисление вариантов должно быть упорядоченным.
Пример 1. Из цифр 2, 4, 7 следует составить трехзначное число, в котором ни одна цифра не может повторяться более двух раз. Сколько таких чисел можно составить?
|
|
|
Решение. Начнем составлять все возможные трехзначные числа, начиная с цифры 2 на первом месте:
224, 227, 242, 244, 247, 272, 274, 277,
422, 424, 427, 442, 447, 472, 474, 477,
722, 724, 727, 742, 744, 747, 772, 774.
В итоге получили 24 числа.
В данной задаче для перечисления вариантов был использован принцип возрастания для чисел.
Другим способом представления перебора вариантов является граф. Так называют геометрические фигуры, состоящие из точек (их называют вершинами) и линий, их соединяющих (называемых ребрами графа). При этом с помощью вершин изображают элементы некоторого множества (предметов, людей, числовых и буквенных кодов и т.п.), а с помощью ребер - определенные связи между этими элементами. Объекты представляются как вершины, или узлы графа, а связи – как дуги, или ребра.
Пример 2. В чемпионате по хоккею участвовало 5 команд. Каждая команда играла с каждой один раз. Сколько всего было игр?
Решение.
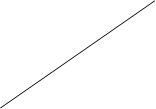








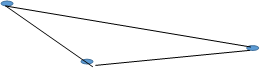
В графе 10 ребер, значит, всего было 10 игр.
Ответ: 10.
|
|
|
Иногда при решении задач необходимо использовать направленные графы. В этом случае появляются взаимно-обратные стрелки на каждом ребре графа.
Пример 3. По окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек было роздано, если во встрече участвовали 5 человек?
Решение.
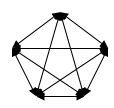
| В графе 10 ребер и 20 стрелок, значит, передано 20 визитных карточек. Ответ: 20. |
Разновидностью графов является дерево возможных вариантов.
Дерево возможных вариантов– граф, схема, отражающая структуру задачи, упорядочения многошагового процесса принятия решений. Ветви дерева отображают различные события, которые могут иметь место, а корень дерева – состояние, в котором возникает необходимость выбора.
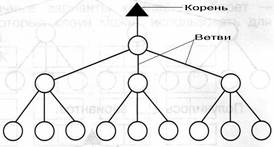
Пример 4. В пакете лежат 3 неразличимых на ощупь шара: два белых и один черный. При вытаскивании черного шара его возвращают обратно, а вытащенный белый шар откладывают в сторону. Такую операцию производят три раза подряд.
а) Нарисовать дерево возможных вариантов.
б) В скольких случаях три извлеченных шара будут одного цвета?
Решение.
а) Дерево возможных вариантов представлено на рисунке.
|
|
|
Случай вытаскивания двух белых шаров особенный. В этом случае остается один черный шар и только его потом можно будет брать.
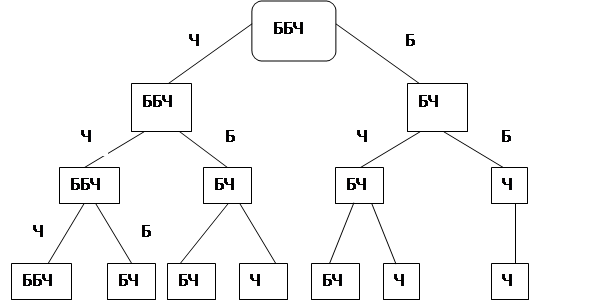
Всего: 7 вариантов
б) По дереву вариантов видно, что это возможно в единственном случае, когда три раза подряд вытаскивается шар черного цвета.
Ответ: а) 7; б) 1.
Еще одним способом представления всех возможных вариантов в задаче является таблица.
Пример 5. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком ли кефиром. Сколько вариантов завтрака есть у Вовы?
Решение. Соберем все варианты в таблицу.
Таблица
| Плюшка | Бутерброд | Пряник | Кекс | |
| Кофе | Кофе, плюшка | Кофе, бутерброд | Кофе, пряник | Кофе, кекс |
| Сок | Сок, плюшка | Сок, бутерброд | Сок, пряник | Сок, кекс |
| Кефир | Кефир, плюшка | Кефир, бутерброд | Кефир, пряник | Кефир, кекс |
Так как выбор еды и напитка происходит независимо, то в каждой ячейке таблицы стоит один из возможных вариантов завтрака. Верно и обратное: любой вариант завтрака будет расположен в одной из ячеек. Значит, всего вариантов столько же, сколько и клеток, то есть 12.
|
|
|
Ответ: 12.
Пример 6. Найти количество всех двузначных чисел, в записи которых используются лишь цифры 1, 2, 3, 4, 5, 6.
Решение. Применим «табличный» способ: все такие числа можно расположить в виде следующей таблицы.
|
| Число оканчивается цифрой | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Число начинается с 1 | 11 | 12 | 13 | 14 | 15 | 16 |
| Число начинается с 2 | 21 | 22 | 23 | 24 | 25 | 26 |
| Число начинается с 3 | 31 | 32 | 33 | 34 | 35 | 36 |
| Число начинается с 4 | 41 | 42 | 43 | 44 | 45 | 46 |
| Число начинается с 5 | 51 | 52 | 53 | 54 | 55 | 56 |
| Число начинается с 6 | 61 | 62 | 63 | 64 | 65 | 66 |
В таблице 6 строк, а в каждой строке по 6 чисел. Следовательно, всего таких чисел 36.
Ответ: 36.
Основные правила комбинаторики
Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правила суммы и правила произведения.
Правило суммы. Если элемент А может быть выбран п1 способами, а элемент В – другими п2 способами, причем выборы А и В являются взаимно исключающими, то выбор «либо А, либо В» может быть осуществлен (п1+ п2) способами.
Правило произведения (умножения). Если элемент А может быть выбран п1 способами, и после каждого из таких выборов элемент В может быть выбран п2 способами, то выбор «А и В» может быть осуществлен (п1∙ п2) способами.
Эти правила позволяют «свернуть» решения многих комбинаторных задач.
Комбинаторные правила суммы и произведения могут быть обобщены на случай произвольного числа последовательных выборов.
Многие комбинаторные задачи решаются прямым применением этих правил. На основе правила произведения выводится формула для числа перестановок.
Пример 1. На клумбе растут 120 цветов, из них 25 – белого цвета, 30 – красного, 20 –синего, остальные – желтого. Сколькими способами можно выбрать небелый цветок?
Решение. Выбранный небелый цветок может быть красным или синим или желтым. Выбор красного цветка может быть сделан п1 способами, п1 =30; выбор синего – п2 способами, п2 =20; выбор желтого – п3 способами, п3 =45. По правилу суммы получаем:
N= n1+n2+n3=30+20+45=95.
Пример 2. В гардеробе выпускника 4 различные рубашки, 3 галстука и 2 костюма. Сколько способов одеться на выпускной вечер у него имеется?
Решение. Чтобы одеться, необходимо выбрать и костюм, и рубашку, и галстук. Выбор костюма может быть сделан п1 способами, п1 =2; выбор рубашки – п2 способами, п2 =4; выбор галстука – п3 способами, п3 =3. По правилу произведения получаем:
N= n1∙n2∙n3=2∙4∙3=24.
Ответ: 24.
Оба правила редко используются обособленно, чаще всего они применяются совместно.
Пример 3. Из цифр 2, 4, 6 и 8 составляют все возможные числа, содержащие не более трех цифр. Сколько существует таких чисел?
Решение. Так как числа не должны содержать более трех цифр, они могут быть либо однозначными, либо двузначными, либо трехзначными. Поэтому чтобы найти число таких чисел нужно использовать правило суммы: N= n1+n2+n3, где n1 – количество однозначных чисел, n2 – количество двузначных чисел, n3 – количество трехзначных чисел.
Ясно что п1 =4, так как это числа 2, 4, 6, 8.
Чтобы определить п2 необходимо воспользоваться правилом умножения. При составлении двузначного числа нужно выбрать его первую цифру (это можно сделать четырьмя способами), а потом вторую (это также можно сделать четырьмя способами). В итоге получим: п2=4∙4=16.
Рассуждая аналогично, найдем: n3=4∙4∙4=64.
Окончательно получим:
N= n1+n2+n3=4+16+64=84.
Ответ: 84.
Дата добавления: 2022-07-02; просмотров: 39; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
