Теорема об условной сходимости градиентного метода с постоянным шагом .

Теорема 1: Пусть в задаче (1) функция f ограничена снизу, непрерывно дифференцируема и, более того, f ′ удовлетворяет условию Липшица :

||f ′(x) – f ′(y)|| ≤ Λ ||x – y|| при всех x, y ∈ Rm.

Тогда при α ∈ (0, 2/Λ) градиентный метод с постоянным шагом условно сходится .

Д о к а з а т е л ь с т в о. Положим zⁿ = –αf ′(xⁿ) и обозначим f(xⁿ + tzⁿ) через φ(t). Тогда, как легко видеть,

φ′(t) = (f ′(xn + tzn), zn)

и поэтому по формуле Ньютона — Лейбница для функции φ

f(xn+1) – f(xn) = f(xn + zn) – f(xn) = φ(1) – φ(0) =

 

= ∫ 1 0 φ′(s) ds = ∫ 1 0 (f ′(xn+ szn), zn) ds.

 

Добавив и отняв (f ′(xn), zn) = ∫01(f ′(xn), zn) ds и воспользовавшись неравенством (x, y) ≤ ||x|| · ||y||, получим

 

f(xn+1) – f(xn) = (f ′(xn), zn) + ∫ 1 0 (f ′(xn + szn) – f ′(xn), zn) ds ≤

 

≤ (f ′(xn), –αf ′(xn)) + ∫ 1 0 ||f ′(xn + szn) – f ′(xn)|| · ||zn|| ds.

Учитывая условие Липшица для f ′, эту цепочку можно продолжить:

f(xn+1) – f(xn) ≤ –α||f ′(xn)||2 + Λ ||zn||2 ∫ 1 0 s ds = = – α||f ′(xn)||2 + Λα2 2 ||f ′(xn)||2 = –α||f ′(xn)||2 ( 1 – Λα 2 ) .

(8)

Поскольку 1 – Λα/2 > 0, последовательность {f(xⁿ)} не возрастает и, следовательно, релаксационность {xⁿ} доказана. А так как в силу условий теоремы f еще и ограничена снизу, последовательность {f(xⁿ)} сходится. Поэтому, в частности, f(xⁿ⁺¹) – f(xⁿ) → 0 при n → ∞. Отсюда и из (8) получаем

||f ′(xn)||2 ≤ α–1 ( 1 – Λα 2 ) –1 [f(xn) – f(xn+1)] → 0 при n → ∞.

Замечания о сходимости.

Подчеркнем, что теорема 1 не гарантирует сходимости метода, но лишь его условную сходимость, причем, локальную. Например, для функции f(x) = (1 + x²)^–1 на R последовательность {xⁿ} градиентного метода с постоянным шагом, начинающаяся с произвольного x⁰ стремится к ∞.

 

З а д а ч а 7. Докажите это.

Поскольку в теореме 1 градиент непрерывен, любая предельная точка последовательности {xⁿ} является стационарной. Однако эта точка вовсе не обязана быть точкой минимума, даже локального. Например, рассмотрим для функции f(x) = x²sign x градиентный метод с шагом α ∈ (0, 1/2). Тогда, как легко видеть, если x⁰ > 0, то xⁿ → 0 при n → ∞. Точка же x = 0 не является локальным минимумом функции f.

Заметим также, что описанный метод не различает точек локального и глобального минимумов. Поэтому для того, чтобы сделать заключение о сходимости xⁿ к точке x* = argmin f(x) приходится налагать дополнительные ограничения, гарантирующие, в частности, существование и единственность решения задачи (1). Один вариант таких ограничений описывается ниже.

Теорема о линейной сходимости градиентного метода с постоянным шагом.

Теорема 2: Пусть выполнены условия теоремы 1. и, кроме того, f дважды непрерывно дифференцируема и сильно выпукла с константой λ. Тогда при α ∈ (0, 2/Λ) градиентный метод с шагом α сходится со скоростью геометрической прогрессии со знаменателем q = max{|1 – αλ|, |1 – αΛ |}:

||xn – x*|| ≤ qn||x0 – x*||.

Д о к а з а т е л ь с т в о. Решение x* = argmin f(x) существует и единственно. Для функции F(x) = f ′(x) воспользуемся аналогом формулы Ньютона — Лейбница

F(y) = F(x) + ∫ 1 0 F ′[x + s(y – x)](y– x) ds.

Далее, f ′′(x) ≤ Λ при всех x ∈ R^m. Кроме того, по условию f ′′(x) ≥ λ при тех же x. Поэтому, так как

λ||h||2 ≤ (f ′′[x* + s(xn –x*)]h, h) ≤ Λ ||h||2,

выполнено неравенство

λ||h||2 ≤ ( ( ∫ 1 0 f ′′[x* + s(xn –x*)] ds ) h, h ) ≤ Λ ||h||2.

(10)

Интеграл, стоящий в этом неравенстве, определяет линейный (симметричный в силу симметричности f) оператор на R^m, обозначим его Lⁿ. Неравенство (10) означает, что λ ≤ Lⁿ ≤ Λ. В силу (9) градиентный метод (4) записывается в виде

xn+1 = xn – αLn(xn – x*).

Спектр σ(I – αLⁿ) оператора I – αLⁿ состоит из чисел вида σ_i = 1 –αλ_i, где λ_i ∈ σ(Lⁿ). В силу (10),

1 – αλ ≥ σi ≥ 1 – αΛ,

и следовательно

||I – αLn|| ≤ max{|1 –αλ|, |1 – αΛ |} = q.

Таким образом,

||xn+1 – xn|| ≤ q||xn – x*||.

Из этого неравенства и задачи 1 вытекает утверждение теоремы.

Об оптимальном выборе шага .

Константа q, фигурирующая в теореме 2. и характеризующая скорость сходимости метода, зависит от шага α. Нетрудно видеть, что величина

q = q(α) = max{|1 – αλ|, |1 – αΛ |}

минимальна, если шаг α выбирается из условия |1 – αλ| = |1 – αΛ | (см. рис. 3), т. е. если α = α* = 2/(λ+ Λ). При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной

q = q* = Λ – λ Λ + λ .

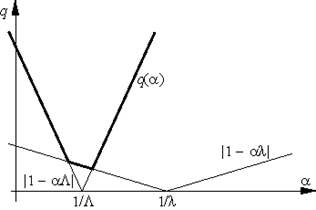
Рис. 3.

В качестве λ и Λ могут выступать равномерные по x оценки сверху и снизу собственных значений оператора f ′′(x). Если λ << Λ, то q* ≈ 1 и метод сходится очень медленно. Геометрически случай λ << Λ соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 4). Простейшим примером такой функции может служить функция на R², задаваемая формулой

f(x1, x2) = λx21+ Λ x22  с λ << Λ.

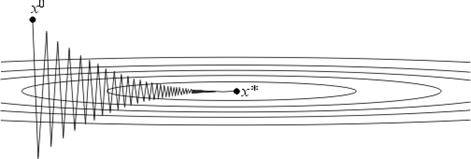
Рис. 4.

Поведение итераций градиентного метода для этой функции изображено на рис. 4 – они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число μ = Λ/λ (характеризующее, грубо говоря, разброс собственных значений оператора f ′′(x)) называют числом обусловленности функции f. Если μ >> 1, то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно.

Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Опишем два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.

---

Дата добавления: 2022-06-11; просмотров: 49; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!