Один пример исследования сходимости.

Градиентные методы

... нет такой воды, которая не стремилась бы [течь] вниз.

Мэн-цзы

Здесь изучается класс так называемых градиентных методов приближенного решения задач оптимизации. Доказываются теоремы сходимости, описываются простейшие модификации.

Общие соображения и определения.

Наиболее распространенные и эффективные методы приближенного решения задачи безусловной оптимизации

f(x) → min,

(1)

где f: R^m → R, укладываются в следующую грубую схему. Начиная с некоторого x⁰ ∈ R^m, строится последовательность {xⁿ} ⊂ R^m такая, что

f(xn+1) < f(xn)

(2)

при всех n ∈ N. Такие последовательности иногда называют релаксационными, а методы построения релаксационных последовательностей – итерационными методами или методами спуска. Последовательность, удовлетворяющую (2), строят в надежде, что уменьшая на каждом шаге (переходе от xⁿ к xⁿ⁺¹) значение функции, мы приближаемся к минимуму (по крайней мере, локальному).

Мы будем говорить, что метод, начиная с данного x⁰ ∈ R^m,

а) условно сходится, если последовательность {xⁿ} релаксационна и

f ′(xn) → Θ при n → ∞;

б) сходится, если

xn → x* = argmin f(x) при n → ∞;

в) линейно сходится (или сходится со скоростью геометрической прогрессии, или имеет первый порядок сходимости), если при некоторых C > 0 и q ∈ [0, 1)

||xn – x*|| ≤ Cqn;

(3)

г) сверхлинейно сходится, если для любого q ∈ (0, 1) и некоторого (зависящего от q) C выполнено неравенство (3);

д) квадратично сходится (или имеет второй порядок сходимости), если при некоторых C > 0 и q ∈ [0, 1) и всех n ∈ N

||xn – x*|| ≤ Cq2n.

Если эти свойства выполняются только для x⁰ достаточно близких к x*, то как всегда добавляется эпитет "локально".

З а д а ч а 1*. Пусть при некотором q ∈ [0, 1)

||xn+1 – x*|| ≤ q||xn – x*||, n ∈ N.

Докажите, что метод линейно сходится.

З а д а ч а 2*. Пусть при некотором C₁ > 0

||xn+1 – x*|| ≤ C1||xn –x*||2, n ∈ N

и ||x⁰ – x*|| достаточно мала. Докажите, что метод квадратично сходится.

Будем говорить, что на данной последовательности метод сходится с порядком p (или имеет p-ый порядок сходимости), если при некотором C

||xn+1 – x*|| ≤ C||xn – x*||p.

Эвристические соображения, приводящие к градиентным методам.

Выше уже отмечалось, что если x не является точкой локального минимума функции f, то двигаясь из x в направлении, противоположном градиенту (еще говорят, в направлении антиградиента), мы можем локально уменьшить значение функции. Этот факт позволяет надеяться, что последовательность {xⁿ}, рекуррентно определяемая формулой

xn+1 = xn – αf ′(xn),

(4)

где α - некоторое положительное число, будет релаксационной.

К этой же формуле приводит и следующее рассуждение. Пусть у нас есть некоторое приближение xⁿ. Заменим в шаре B(xⁿ, ε) с центром в точке xⁿ функцию f ее линейным (вернее, афинным) приближением:

f(x) ≈ φ(x) ≝ f(xn) + (f ′(xn), x – xn)                              (4*)

(функция φ аппроксимирует f в окрестности точки xⁿ с точностью o(x – xⁿ)). Разумеется, (линейная) безусловная задача φ(x) → min неразрешима, если f ′(xⁿ) ≠ Θ. В окрестности же B(xⁿ, ε) функция φ имеет точку минимума. Эту точку естественно взять за следующее приближение xⁿ⁺¹.

Градиентный метод с постоянным шагом.

В общем случае число α в формуле (4) может на каждом шаге (т. е. для каждого n) выбираться заново:

xn+1 = xn – αnf ′(xn).

(5)

Именно методы, задаваемые формулой (5), называются градентными. Если αⁿ = α при всех n, то получающийся метод называется градиентным методом с постоянным шагом (с шагом α.)

Поясним геометрическую суть градиентного метода. Для этого мы выберем способ изображения функции с помощью линий уровня. Линией уровня функции f (изолинией) называется любое множество вида {x ∈ R^m: f(x) = c}. Каждому значению c отвечает своя линия уровня (см. рис. 1).

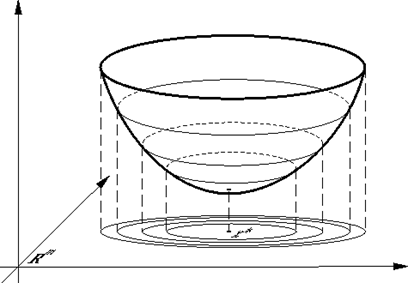
Рис. 1.

З а д а ч а 3. Докажите, что касательная к линии уровня функции f: R² → R ортогональна к градиенту. Как обобщить это утверждение на многомерный случай?

Геометрическая интерпретация градиентного метода с постоянным шагом изображена на рис. 2. На каждом шаге мы сдвигаемся по вектору антиградиента, "уменьшенному в α раз".

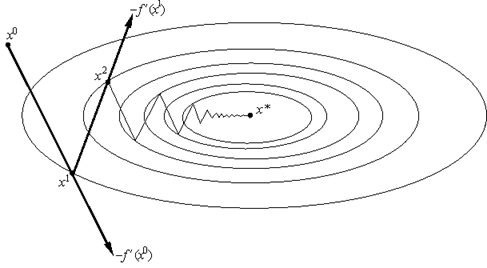
Рис. 2.

Один пример исследования сходимости.

Изучим сходимость градиентного метода с постоянным шагом на примере функции

f(x) = |x|p,

где p > 1 (случай p ≤ 1 мы не рассматриваем, поскольку тогда функция f не будет гладкой, а мы такой случай не исследуем). Очевидно, задача (1) с такой функцией f имеет единственное решение x* = 0. Для этой функции приближения xⁿ градиентного метода имеют вид:

xn+1 = xn – αp|xn|p–1sign xn.

(6)

Пределом этой последовательности может быть только 0. Действительно, если x** = lim_n→∞ xⁿ ≠ 0, то, переходя к пределу в (6) при n → ∞, получаем противоречащее предположению x** ≠ 0 равенство

x** = x** – αp|x**|p–1sign x**,

откуда x** = 0. Очевидно также, что если x⁰ = 0, то и xⁿ = 0 при всех n.

Покажем, что если p < 2, то при любом шаге α > 0 и любом начальном приближении x⁰ (за исключением не более чем счетного числа точек) приближения (6) не являются сходящимися. Для этого заметим, что если 0 < |xⁿ| < (2/αp)^1/2(2–p), то

|xn+1| > |xn|.

(7)

Поэтому, если xⁿ не обращается в нуль, то она не может сходиться к нулю и, следовательно, не может сходиться вообще.

З а д а ч а 4. Докажите.

Таким образом, осталось доказать (7). В силу (6)

|xn+1| = |xn – αp|xn|p–1 ·sign xn| = |xn|·| 1 –αp|xn|p–2·sign xn|.

Остается заметить, что если 0 < |xⁿ| < (2/αp)^1/(2–p), то, как нетрудно видеть, |1 – αp|xⁿ|^p–2·sign xⁿ| > 1, что и требовалось.

З а д а ч а 5. Покажите, что число начальных точек x⁰, для которых xⁿ обращается в нуль при некотором n (и, следовательно, при всех бóльших), не более чем счетно.

Если p = 2, т. е. f(x) = x², то (6) переписывается в виде

|xn+1| = |xn|·|1 – 2α|.

Поэтому, если α ∈ (0, 1), то |1 – 2α| < 1, а следовательно,

|xn+1| = |1 – 2α|n+1·|x0| → 0 при n → ∞.

Если же α ≥ 1, то

|xn+1| ≥ |xn|,

и последовательность {xⁿ}, начинающаяся из ненулевой начальной точки, расходится.

З а д а ч а 6. Докажите, что если p > 2, то градиентный метод (6) сходится при αp|x⁰|^p–2 < 2 и расходится при αp|x⁰|^p–2 ≥ 2 для любых начальных точек, за исключением может быть счетного множества.

Таким образом, есть функции, для которых градиентный метод не сходится даже при сколь угодно малом шаге α и есть функции, для которых он сходится только при достаточно малых шагах. В следующих пунктах мы приведем ряд теорем о сходимости градиентного метода.

 

---

Дата добавления: 2022-06-11; просмотров: 29; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!