Система оценивания экзаменационной работы по математике
Профильный уровень
Каждое из заданий 1 – 12 считается выполненным верно, если экзаменуемый дал верный ответ. Каждое верно выполненное задание оценивается 1 баллом.
| Номер задания | Правильный ответ | |||
| Пример 1 | Пример 2 | Пример 3 | Пример 4 | |
| 1 | 8 | 5 | 133 | 13 |
| 2 | 9 | 2 | 4 | |
| 3 | 6 | 6 | ||
| 4 | 0,08 | 0,2 | 0,657 | |
| 5 | 9 | 17 | 93 | 3 |
| 6 | 64 | 6 | 154 | 16 |
| 7 | 4 | -1,75 | ||
| 8 | 4 | 12 | 52 | |
| 9 | -0,96 | 4 | 16 | |
| 10 | 751 | |||
| 11 | 5 | 15 | 7,5 | 72 |
| 12 | -83 | -6 | 16 | 1,5 |
Решения и критерии оценивания выполнения задания с развернутым ответом
Количество баллов, выставленных за выполнение заданий 13–19, зависит от полноты решения и правильности ответа.
Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным; все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается 0 баллов.
Эксперты проверяют только математическое содержание представленного решения, а особенности записи не учитывают.
При выполнении задания могут использоваться без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования
|
|
|
Решения и критерии оценивания заданий 13 – 19.
Каждое верно выполненное задание оценивается 2 баллами.
13. а) Решите уравнение 
.
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Решение
Запишем исходное уравнение в виде:
Значит,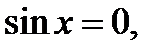 
откуда 
, 
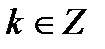, или 
откуда или, 
или 
, 
.
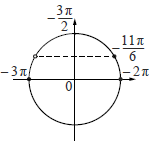б) С помощью числовой окружности отберем корни, принадлежащие отрезку 
.
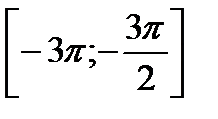Получим числа: 
; 
; 
.
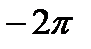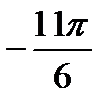Ответ: а)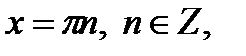 
; 
, 
.
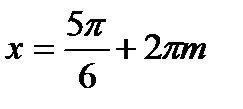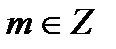б) ; ; .
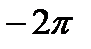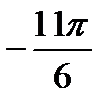14. Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N— середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
|
|
|
б) Найдите угол между плоскостями BMN и ABB1.
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в пунктах а и б | 2 |
| Выполнен только один из пунктов – а или б ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов а) и б)» | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 2 |
Решение
а) Пусть точка H — середина AC . Тогда
.
Вместе с тем
,
тогда по теореме, обратной теореме Пифагора, треугольник BMN является прямоугольным с прямым углом М.
б) Проведем перпендикуляр NP к прямой А1В1. Тогда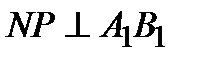 
и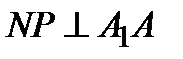 
. Следовательно 
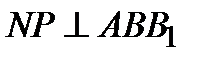. Поэтому МР – проекция МN на плоскость 
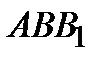. Прямая ВМ перпендикулярна МN, тогда по теореме о трех перпендикулярах 
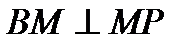. Следовательно, угол NMP – линейный угол искомого угла.
Длина NP равна половине высоты треугольника А1В1С1, т.е. 
.
Поэтому 
.
Следовательно,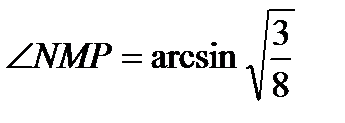 
.
Ответ: б)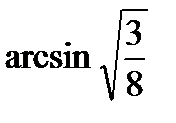 
.
ИЛИ
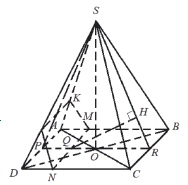В правильной четырёхугольной пирамиде SABCD сторона АВ основания равна 16, а высота пирамиды равна 4. На рёбрах АВ , CD и AS отмечены точки M , N и K соответственно, причём AM = DN = 4 и AK = 3.
|
|
|
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC .
Решение
а) Пусть О – центр основания пирамиды. Тогда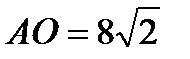 
, 
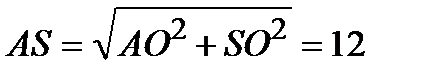. Следовательно, АМ : АВ = АК : AS = 1 : 4, поэтому прямые SB и КМ параллельны. Кроме того, MBCN – прямоугольник, поэтому прямые MN и ВС также параллельны. Отсюда следует, что плоскость MNK и SBC параллельны.
б) Пусть P, Q, R – середины отрезков AD, MN и ВС соответственно. Тогда плоскость SPR перпендикулярна прямой ВС, а по доказанному в п. а) плоскости MNK и SBC параллельны, поэтому искомое расстояние равно расстоянию от точки Q до плоскости SBC. Проведем из точки Q перпендикуляр QН к прямой SR.
Тогда 
.
Ответ: б) 
.
15. Решите неравенство: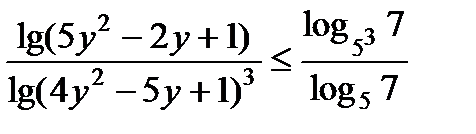 
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ. | 2 |
| Допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения. ИЛИ недостаточное обоснование решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Решение
Используя свойства логарифмов, преобразуем неравенство:
|
|
|
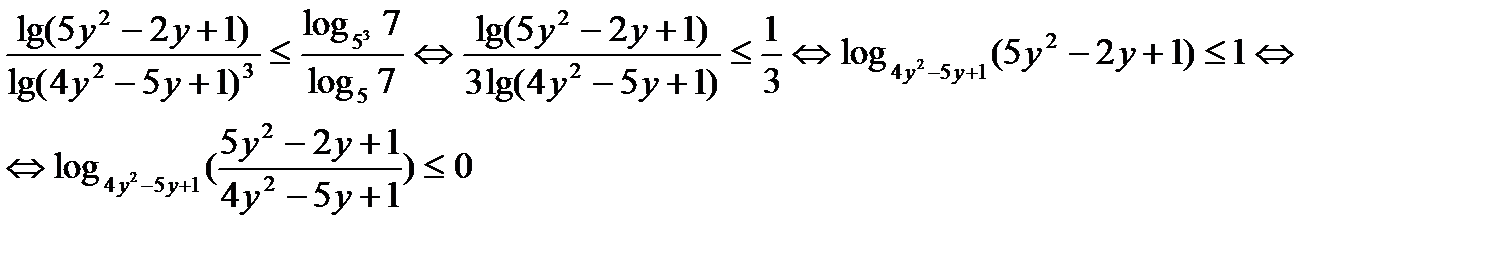
Перейдём к системе:
Решение первого неравенства: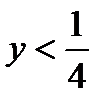 
или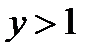 
. Из второго равенства получаем, что 
и 
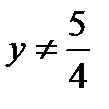Решение третьего неравенства: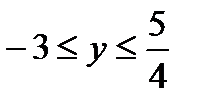 
Таким образом, решением неравенства является: 
Ответ: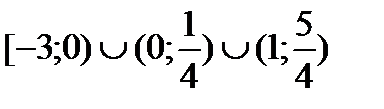 
Каждое верно выполненное задание оценивается 3 баллами.
16. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
| Критерии оценивания выполнения задания | Баллы |
| Имеется верное доказательство утверждения пункта а, и обоснованно получен верный ответ в пункте б | 3 |
| Получен обоснованный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а, и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а ИЛИ при обосновании решения пункта б получен неверный ответ из-за арифметической ошибки ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведенных выше | 0 |
| Максимальный балл | 3 |
Решение
а) Обозначим центры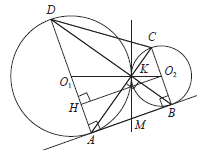 
окружностей О1 и О2 соответственно.
Пусть общая касательная, проведённая к окружностям в точке K , пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный. AD 
AB. Аналогично получаем, что BC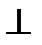 
AB. Следовательно, прямые AD и BC параллельны.
б) Пусть, для определённости, первая окружность имеет радиус 4, а вторая — радиус 1.
Треугольники BKC и AKD подобны,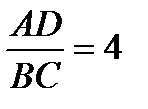 
. Пусть 
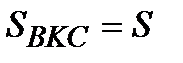, тогда 
.
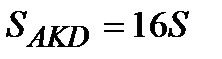У треугольников AKD и AKB общая высота, следовательно, следовательно,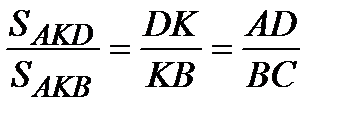 
, т.е. 
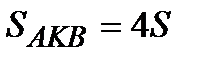. Аналогично, 
. Площадь трапеции ABCD равна 25S. Вычислим площадь трапеции ABCD. Проведем к AD перпендикуляр О2Н, равный высоте трапеции, и найдем его из прямоугольного треугольника О2НО1:
.
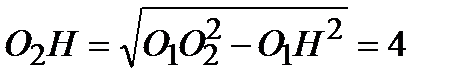Тогда
.
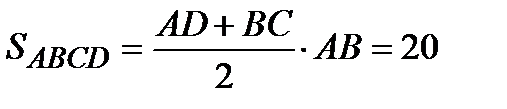Следовательно, 25S = 20, откуда S = 0,8 и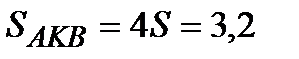 
.
Ответ: 3,2.
17. 15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
–15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ | 3 |
| Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: - неверный ответ из-за вычислительной ошибки; - верный ответ, но решение недостаточно обосновано | 2 |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Решение
Пусть сумма кредита A тысяч рублей. По условию, долг перед банком (в тыс. рублей) по состоянию на 15-е число должен уменьшаться до нуля следующим образом:
А, А − 30, А − 60, ..., А − 570, А − 600, 0.
Первого числа каждого месяца долг возрастает на 3%, значит, последовательность размеров долга (в тыс. рублей) по состоянию на 1-е число такова:
1,03А, 1,03(А − 30), ..., 1,03(А − 570), 1,03(А − 600).
Следовательно, выплаты (в тыс. рублей) должны быть следующими:
0,03А + 30, 0,03(А − 30) + 30, ..., 0,03(А − 570) + 30, 1,03(А − 600).
Всего следует выплатить
(тыс. рублей).
Откуда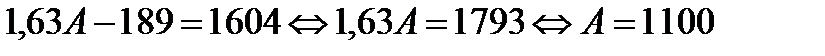 
Значит, сумма, которую планируется взять в кредит равна 1100 тыс. рублей.
Ответ: 1100 тыс. рублей.
ИЛИ
Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны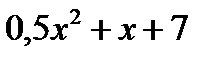 
млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит 
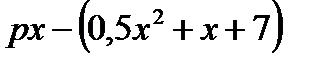. Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
Решение
Прибыль фирмы (в млн рублей) за один год выражается как
Это выражение является квадратным трехчленом и достигает своего наибольшего значения при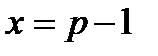 
. Наибольшее значение равно 
.
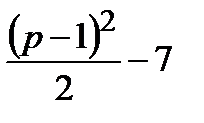Строительство завода окупится не более чем за 3 года, если
; 
; 
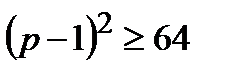, то есть при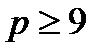 
, поскольку цена продукции не может быть отрицательной.
Таким образом, наименьшее значение р = 9.
Ответ: р = 9.
Каждое верно выполненное задание оценивается 4 баллами.
18. Найдите все положительные значения a , при каждом из которых система
имеет единственное решение.
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены оба верных значения параметра, но – или в ответ включены также и одно-два неверных значения; – или решение недостаточно обосновано | 3 |
| С помощью верного рассуждения получено хотя бы одно верное значение параметра | 2 |
| Задача сведена к исследованию: – или взаимного расположения трёх окружностей; – или двух квадратных уравнений с параметром | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Решение
Если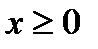 
, то уравнение 
задает окружность 
1 с центром в точке С1(5; 4) радиусом 3, а если х < 0, то оно задает окружность 2 с центром в точке С2(-5; 4) таким же радиусом (см. рисунок)
При положительных значениях а уравнение 
задает окружность с центром в точке С(-2; 0) радиуса а. Поэтому задача состоит в том, чтобы найти все значения а, при каждом из которых окружность имеет единственную общую точку с объединением окружностей 1 и 2.
Из точки С проведем луч СС1 и обозначим через А1 и В1 точки его пересечения с окружностью 1, где А1 лежит между С и С1. Так как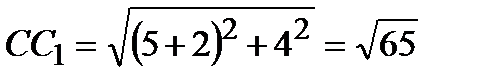 
, то 
, 
.
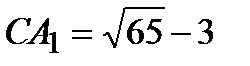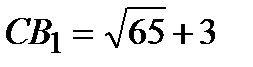При а < СА1 или а > СВ1 окружности и 1 не пересекаются.
При СА1 < а < СВ1 окружности и 1 имеют две общие точки.
При а = СА1 или а = СВ1 окружности и 1 касаются.
Из точки С проведем луч СС2 и обозначим через А2 и В2 точки его пересечения с окружностью 2, где А2 лежит между С и С2. Так как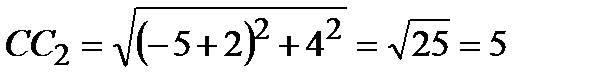 
, то 
, 
.
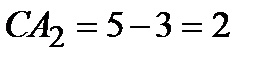При а < СА2 или а > СВ2 окружности и 2 не пересекаются.
При СА2 < а < СВ2 окружности и 2 имеют две общие точки.
При а = СА2 или а = СВ2 окружности и 2 касаются.
Исходная система имеет единственное решение тогда и только тогда, когда окружность касается ровно одной из двух окружностей 1 и 2 и не пересекается с другой. Так как СА2 < СА1 < СВ2 < СВ1, то условию задачи удовлетворяют только числа а = 2 и 
.
Ответ: 2;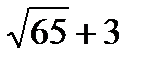 
.
19. В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали, по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
| Критерии оценивания выполнения задания | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов ИЛИ при правильном ходе решения допущены вычислительная ошибка | 2 |
| Верно получен один из следующих результатов: – обоснованное решение пункта а; – обоснованное решение пункта б; – искомая оценка в пункте в; – пример в пункте в, обеспечивающий точность предыдущей оценки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Решение
а) Пусть в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал 19 баллов и перешёл в школу № 2. Тогда средний балл в школе № 1 уменьшился в 10 раз.
б) Пусть в школе № 2 писали тест m учащихся, средний балл равнялся B , а перешедший в неё учащийся набрал u баллов. Тогда получаем:
;
.
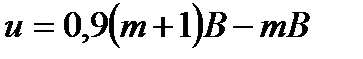Если B = 7, то (9 − m)B не делится на 10, а 10u делится на 10. Но это невозможно, поскольку 10u = (9 − m)B .
в) Пусть в школе № 1 средний балл равнялся A. Тогда получаем:
u = (9 − m) A − 0,9(8 − m) A; 10u = (18 − m) A = (9 − m)B .
Заметим, что если B =1 или B = 3, то 10u = (9 − m)B не делится на 10. Если B = 2 или B = 4 , то m = 4 . В первом случае 14A =10 , а во втором 14A = 20 . Значит, ни один из этих случаев не возможен.
При B = 5 и m = 3 получаем u = 3 и A = 2 . Этот случай реализуется, например, если в школе № 1 писали тест 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, в школе № 2 писали тест 3 учащихся и каждый набрал по 5 баллов, а у перешедшего из одной школы в другую учащегося – 3 балла.
Ответ: а) да; б) нет; в) 5.
ИЛИ
На доске написаны десять различных натуральных чисел, которые удовлетворяют двум условиям: среднее арифметическое шести наименьших из них равно 5, а среднее арифметическое шести наибольших равно 15.
а) Может ли наименьшее из этих десяти чисел равняться 3?
б) Может ли среднее арифметическое всех этих десяти чисел равняться 11?
в) Каково наибольшее возможное значение среднего арифметического всех этих десяти чисел при данных условиях?
Решение
а) Наименьшее число не может равняться 3, так как в противном случае сумма шести наименьших чисел будет не меньше 3 + 4 + 5 + 6 + 7 + 8 = 33, а их среднее арифметическое – не меньше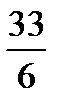 
< 5, что противоречит условию.
б) Пусть a1,a2,...,a10 — написанные на доске числа, расположенные в порядке возрастания. Тогда из условия вытекают равенства a1 + a2 + ...+ a6 = 30, a5 + a6 + ...+ a10 = 90.
Если среднее арифметическое всех чисел равно 11, то a1 + a2 + ...+ a10 =110, откуда
a5 + a6 = (a1 + ...+ a6 ) + (a5 + ...+ a10 ) − (a1 + ...+ a10 ) = 30 + 90 −110 =10, что невозможно, так как a5 ≥ 5 и a6 ≥ 6 .
в) Покажем, что a5 + a6 ≥15. Действительно, если a5 + a6 ≤14, то a1 + a2 + a3 + a4 ≥ 30 −14 =16,
но тогда a4 ≥ 6 (так как иначе a1 + a2 + a3 + a4 ≤ 2 + 3 + 4 + 5 =14) и поэтому
14 ≥ a5 + a6 ≥ 7 + 8 =15 — противоречие.
Таким образом, получаем a1 + a2 + ...+ a10 =120 − (a5 + a6 ) ≤ 105, а значит, среднее арифметическое всех 10 чисел не превосходит значения 10,5.
Это значение реализуется: все условия задачи выполнены для чисел 2, 3, 4, 6, 7, 8, 9, 21, 22, 23, а их среднее арифметическое равно как раз 10,5.
Ответ: а) нет; б) нет; в) 10,5.
Дата добавления: 2022-06-11; просмотров: 116; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!