Решение типовой задачи – элементарные методы выявления взаимосвязей
Лабораторная работа № 6 - Статистическое изучение взаимосвязи социально-экономических явлений
Цели и задачи лабораторной работ
Цель работы - является ознакомление студентов с основными методами выявления и измерения корреляционной связи, при этом будут решаться следующие задачи:
1) Ознакомится с алгоритмом построения корреляционного поля;
2) Рассмотреть методы выявления взаимосвязи;
3) Рассмотреть коэффициенты измерения корреляционной взаимосвязи;
4) Построить регрессионную модель и провести на ее основе моделирование.
Теоретические основы изучения взаимосвязей социально-экономических явлений
В экономических исследованиях различают следующие варианты зависимостей:
Парная - связь между двумя признаками, один из которых результативный, а другой факторный.
| x |
| y |
Рисунок 6.1 – Пример парной корреляции
Частная - зависимость между результативным и одним факторным признаком, при фиксированном значении других факторных признаков.
| y |
| x 1 x 2 x 3 |
Рисунок 6.2 – Пример частной корреляции
Множественная - зависимость результативного признака от нескольких факторных признаков.
| y |
| x 1 |
| x 2 |
| x 3 |
Рисунок 6.3 – Пример множественной корреляции
Каноническая - зависимость группы результативного признака от группы факторных признаков.
| x 1 x 2 x 3 |
| y 1 y 2 y 3 |
Рисунок 6.4 – Пример канонической корреляции
|
|
|
Для выявления и измерения силы взаимосвязи в эконометрике используют ряд подходов:
Элементарные методы (приближенные)
Сопоставление двух параллельных рядов
Построение аналитической группировки
Графический метод
Точные методы
Парные коэффициенты корреляции
Частные коэффициенты корреляции
Множественные коэффициенты корреляции
Подходы к выявлению и измерению корреляционной взаимосвязи
Рисунок 6.5 – Подходы к измерению корреляционной связи
Кратко раскроем сущность представленных методов:
По-видимому, самым простым способом установления наличия взаимосвязи между двумя признаками является графический метод. Суть его заключается в построение поля корреляции, где по оси OX откладывают значения независимой переменной, а по оси OY значения зависимой.
Возможны несколько вариантов расположения точек на данном графике:
| Рис. а прямая взаимосвязь |

|
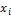
|
| Рис. б обратная взаимосвязь |
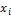
|

|
| Рис. в нелинейная взаимосвязь |
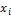
|

|
| Рис. г отсутствие взаимосвязи |
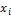
|

|
Рисунок 6.6 – Варианты распределения точек в корреляционном поле
Сопоставление двух параллельных рядов. Значения факторного признака располагают в возрастающем порядке и затем прослеживают направление изменения величины результативного признака.
|
|
|
Возможны три варианта взаимного сочетания переменных:
1. 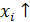 при этом
при этом  - можно предположить наличие прямой взаимосвязи;
- можно предположить наличие прямой взаимосвязи;
2. 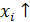 при этом
при этом 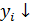 - можно предположить наличие обратной взаимосвязи;
- можно предположить наличие обратной взаимосвязи;
3. 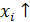 при этом
при этом 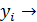 - можно предположить отсутствие взаимосвязи.
- можно предположить отсутствие взаимосвязи.
Построение аналитической группировки, где все наблюдения разбиваются на группы по величине факторного признака, и по каждой группе вычисляется среднее значение результативного признака.
Возможны три варианта взаимного сочетания групповых средних:
1. 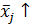 при этом
при этом 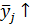 - можно предположить наличие прямой взаимосвязи;
- можно предположить наличие прямой взаимосвязи;
2. 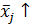 при этом
при этом  - можно предположить наличие обратной взаимосвязи;
- можно предположить наличие обратной взаимосвязи;
3. 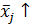 при этом
при этом 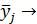 - можно предположить отсутствие взаимосвязи.
- можно предположить отсутствие взаимосвязи.
Приведенные подходы имеют ряд недостатков: во-первых, с их помощью возможно лишь выявить взаимосвязь, но не измерить ее; во-вторых, использование данных методов ограничено лишь парной корреляцией.
Более совершенным подходом считается расчет коэффициентов корреляции.
Таблица 6.1 – Коэффициенты корреляции
|
|
|
| Название | Формула для расчета | Интервал значения | Для какого типа данных используется | ||
| Коэффициент ассоциации Д. Юла | 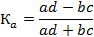 а, b , с, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков
а, b , с, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков
| |Ка| > 0,5 - связь значима | качественные альтернативные признаки | ||
| Коэффициент контингенции К. Пирсона | 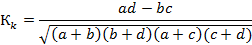
| |Кк| >0,3 - связь значима | качественные альтернативные признаки | ||
| Коэффициент корреляции рангов Чарльза Эдварда Спирмена | 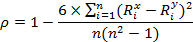
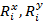 - ранги по результативному и факторному признаку - ранги по результативному и факторному признаку
| [-1; +1] | качественные или количественные ранжируемые признаками | ||
| Коэффициент корреляции знаков Густава Теодора Фехнера |  C - число совпадений знаков H - число несовпадений знаков отклонений индивидуальных величин от средней
C - число совпадений знаков H - число несовпадений знаков отклонений индивидуальных величин от средней
| [-1; +1] | количественные признаками | ||
| Коэффициент линейной корреляции Карла Пирсона | 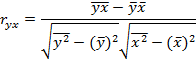
| [-1; +1] | количественные признаками | ||
| Коэффициент взаимной сопряженности К. Пирсона | 
 - показатель взаимной сопряженности - показатель взаимной сопряженности
| [0; +1] | качественные признаки | ||
| Коэффициент взаимной сопряженности А.А. Чупрова | 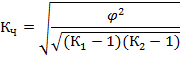 К1, К2 – число строк и граф в таблице
К1, К2 – число строк и граф в таблице
| [0; +1] | качественные признаки | ||
| Множественный коэффициент ранговой корреляции М. Кендэла и Б. Смита |  S - сумма квадратов отклонений суммы m рангов от их средней величины; m - число ранжируемых признаков; n - число ранжируемых единиц (число наблюдений).
S - сумма квадратов отклонений суммы m рангов от их средней величины; m - число ранжируемых признаков; n - число ранжируемых единиц (число наблюдений).
| [0;+1] | качественные признаки | ||
| Множественный коэффициент корреляции | 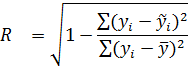
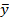 - среднее значение зависимой переменной; - среднее значение зависимой переменной; 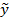 – теоретические значения – теоретические значения
| [0;+1] | количественные признаками | ||
| Частные коэффициенты корреляции (
| 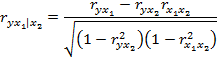
| [0;+1] | количественные признаками | ||
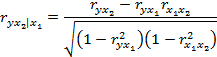
| |||||
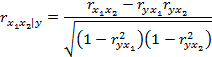
|
Для интерпретации результатов оценки коэффициентов корреляции на практике часто используется шкала Чеддока.
Таблица 6.2 – Сила корреляционной связи по шкале Чеддока
| Показания тесноты связи | до ±0,3 | от ±0,3 до ±0,5 | от ±0,5 до ±0,7 | от ±0,7 до ±0,9 | от ±0,9 до ±0,99 |
| Характеристика связи | слабая | умеренная | заметная | высокая | весьма высокая |
Знак коэффициента указывает на направление связи между исследуемыми признаками, так «-» указывает на обратную связь (рисунок 2.6(а)), а «+» указывает на прямую связь (рисунок 2.6(б)).
Если в ходе исследования значение коэффициента строго равно нулю это указывает на то, что между признаками отсутствует взаимосвязь, соответственно в случае, когда коэффициент равен ±1 взаимосвязь носит функциональный характер.
Как известно из курса эконометрики относительно формы зависимости выделяют линейную и не линейную регрессии, при этом относительно числа независимых переменных включенных в модель выделяют – парную и множественную.
Корреляционный анализ как правило дополняется регрессионным, заключающимся в построении линейных или не линейных, парных или множественных уравнений. В данной лабораторной работе остановимся на самом простом случае на линейной модели.
Множественная линейная регрессия представляет собой модель зависимости результативного признака с двумя и большим числом факторов, т. е. модель вида:
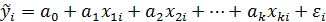
Парная линейная регрессия представляет собой частный случай множественной регрессии и есть модель между двумя переменными - у и х, т.е. имеем:
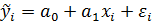
где: i =1, 2, …, n
n – объем изучаемой совокупности;
 – данные полученные в результате построения модели (теоретические уровни, модельные данные)
– данные полученные в результате построения модели (теоретические уровни, модельные данные)
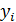 – зависимая переменная;
– зависимая переменная;
 – независимая переменная;
– независимая переменная;
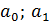 – искомые (неизвестные) параметры (коэффициенты) уравнения регрессии;
– искомые (неизвестные) параметры (коэффициенты) уравнения регрессии;
 – случайная величина (возмущение, остатки, отклонения).
– случайная величина (возмущение, остатки, отклонения).
Основным методом решения задачи нахождения параметров  уравнения связи является метод наименьших квадратов (МНК).
уравнения связи является метод наименьших квадратов (МНК).
Суть МНК состоит в минимизации суммы квадратов отклонений фактических значений от значений, вычисленных по уравнению связи.
 или
или 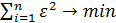
В случае парной линейной регрессии для нахождения 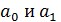 необходимо решить систему нормальных уравнений:
необходимо решить систему нормальных уравнений:

Преобразуя предложенную систему получить следующие формулы для нахождения параметров уравнения:
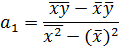
| и | 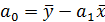
|
 – не имеет экономической интерпретации, но существует мнение, что он показывает усредненное влияние всех прочих факторов, не включенных в исследование.
– не имеет экономической интерпретации, но существует мнение, что он показывает усредненное влияние всех прочих факторов, не включенных в исследование.
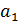 – показывает, на сколько в среднем изменится величина результативного признака y при изменении факторного признака x на натуральную единицу.
– показывает, на сколько в среднем изменится величина результативного признака y при изменении факторного признака x на натуральную единицу.
Если 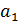 >0 то связь прямая, если
>0 то связь прямая, если 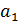 < 0 то связь обратная.
< 0 то связь обратная.
В случае множественной линейной регрессии система нормальных уравнений значительно увеличивается, так в случае двух независимых переменных имеем следующую систему:
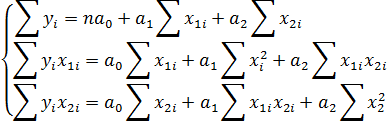
Для ее решения относительно неизвестных параметров 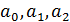 можно поступить несколькими способами:
можно поступить несколькими способами:
1. Использовать возможности специализированных пакетов программ (Excel, Stata, Statistica, MathCad и др.).
2. Использовать решение системы посредством матричной алгебры:
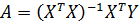
где: 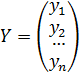
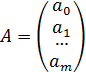
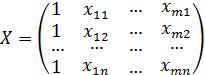
3. Использовать для нахождения параметров общий и частные определители системы.
Общий определитель системы равен:

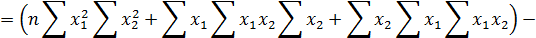
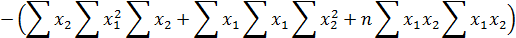
Частные определители:
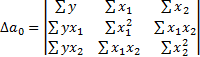
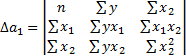

Решение системы может быль осуществлено методом определителей:
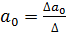 ;
; 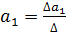 ;
; 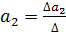
где:  - определитель системы;
- определитель системы;
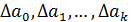 – частные определители.
– частные определители.
Решение типовой задачи – элементарные методы выявления взаимосвязей
Проиллюстрируем алгоритм выявления наличия взаимосвязи между социально-экономическими явлениями на основе следующих данных:
Таблица 6.3 – Вариация показателей характеризующих результаты экономической деятельности промышленных предприятий
| y | 12,3 | 9,9 | 15,1 | 10,4 | 13,1 | 12,4 | 13,2 | 11,8 | 11,5 | 14,2 | 14,4 | 12,1 | 13,1 | 11,5 | 10,6 |
| x1 | 280 | 210 | 323 | 221 | 295 | 271 | 276 | 284 | 260 | 310 | 293 | 239 | 254 | 240 | 246 |
| x2 | 3,12 | 1,25 | 4,98 | 1,35 | 3,25 | 2,99 | 3,69 | 2,65 | 2,1 | 3,75 | 4,57 | 2,94 | 3,56 | 2,24 | 1,45 |
где: y – Чистая прибыль, млн. руб.
 – Численности промышленно-производственного персонала, чел
– Численности промышленно-производственного персонала, чел
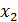 – Среднегодовой стоимости основных производственных фондов, млн. руб.
– Среднегодовой стоимости основных производственных фондов, млн. руб.
Для построения корреляционного поля необходимо по оси OY отложить значения переменной y, а по оси OX отложить значения переменной  .
.
При построении данного графика рекомендуется откладывать значения показателя не от нуля, а от минимального значения показателя, в этом случае график будет информативен. В рассматриваемом примере минимальное значение переменной y наблюдается у второго предприятия равное 9,9 млн. руб., соответственно начало отсчета необходимо начинать от значения 9. По переменной  минимальное значение равно 210 чел. соответственно откладывать необходимо от 200.
минимальное значение равно 210 чел. соответственно откладывать необходимо от 200.
В главном меню табличного редактора Excel выберем Вставка ® Диаграмма, в появившемся окне Мастера диаграмм выберем Точечная, в результате получим следующий график характеризующий зависимость y от  .
.
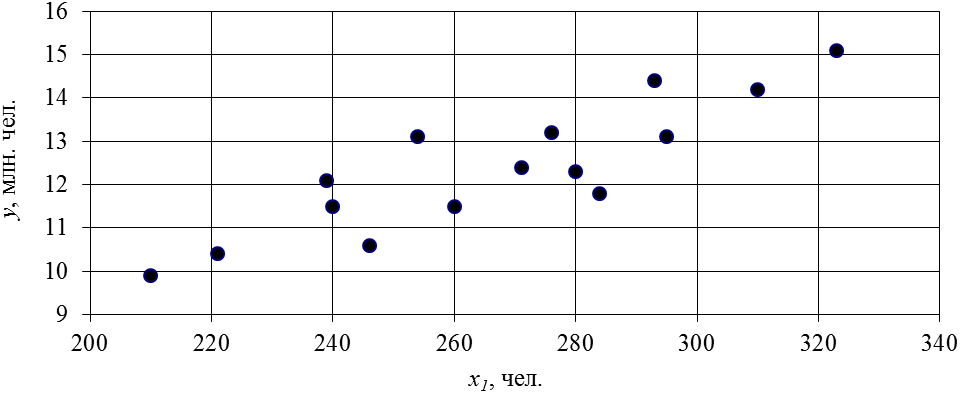
Рисунок 6.7 – Корреляционное поле зависимости чистой прибыли от численности промышленно-производственного персонала
Согласно приведенному рисунку наблюдается рост показателя y с ростом показателя  , т.е. можно предположить о наличии прямой связи между рассматриваемыми показателями.
, т.е. можно предположить о наличии прямой связи между рассматриваемыми показателями.
Для реализации метода сопоставления параллельных рядов, необходимо упорядочить совокупность по переменной 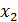 в возрастающем порядке, при этом автоматически будем переносить значения по переменной y соответствующего предприятия. Для этого в главном меню выбираем Данные ® Сортировка. В появившемся окне (рисунок 6.8) указываем переменную
в возрастающем порядке, при этом автоматически будем переносить значения по переменной y соответствующего предприятия. Для этого в главном меню выбираем Данные ® Сортировка. В появившемся окне (рисунок 6.8) указываем переменную 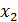 и нажимаем ОК.
и нажимаем ОК.
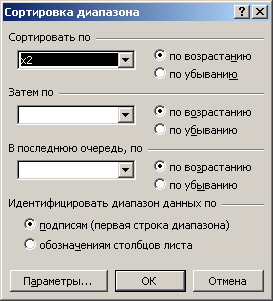
Рисунок 6.8 – Сортировка диапазона
В результате осуществления данной процедуры получаем следующие результаты:

Рисунок 6.9 – Результаты выполнения метода сопоставления параллельных рядов
Результаты реализации процедуры сопоставления параллельных рядов при большом объеме совокупности (если приведены в виде таблицы) не информативны, поэтому рекомендуется приводить их в виде графика, при этом для увеличения информативности рисунка рассматриваемые данные необходимо размещать на разных осях, в нашем случае по оси OY отложим переменную y, а по оси OY 1 - 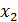 . Т.е. выберем Вставка ® Диаграмма ® Мастер диаграмм ® График.
. Т.е. выберем Вставка ® Диаграмма ® Мастер диаграмм ® График.
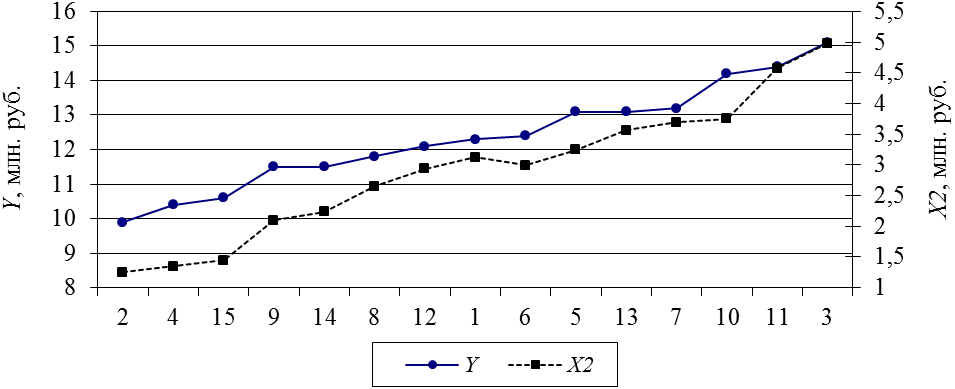
Рисунок 6.10 - Результаты выполнения метода сопоставления параллельных рядов
Результаты, отображенные на рисунке 6.10, указывают на наличие прямой связи между показателями.
Дата добавления: 2022-06-11; просмотров: 59; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

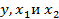 )
)