Уравнение колебаний для математического маятника можно вывести, используя уравнение динамики вращательного движения.

Проведём ось  Z  через точку подвеса перпендикулярно плоскости колебаний маятника, тогда момент инерции материальной точки относительно оси  Z: 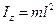, момент импульса точки  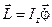 направлен вдоль оси  Z, а момент силы тяжести  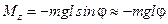(плечо силы тяжести относительно оси равно 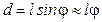) направлен против оси Z.

Закон вращательного движения точки вокруг оси  Z: 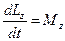  или .§

 

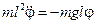Пример. Найдем период колебаний физического маятника - тела массы m, которое может совершать колебания под действием силы тяжести (инерции) вокруг горизонтальной оси, не проходящей через центр масс тела.Сопротивлением воздуха пренебрегаем.

Решение. Проведем из центра масс тела C перпендикуляр к оси вращения z. Пусть длина этого перпендикуляра равна l.

Положение тела зададим углом отклонения j от вертикали этого перпендикуляра.  При этом если угол  j  увеличивается (тело поворачивается против часовой стрелки), то вектор момента импульса 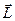 направлен вдоль горизонтальной оси z на нас. Момент внешней силы тяжести относительно оси  z  направлен от нас. Рассмотрим проекции на ось  z: , .

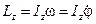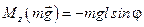Уравнение вращения вокруг оси   z: 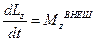   или .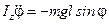

Если выполняется условие малости колебаний: 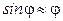, то уравнение колебаний примет вид:

                                                             .

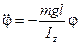С учетом выражения для циклической частоты 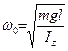 получаем выражение для периода колебаний физического маятника: .

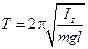Приведённой длиной физического маятника называется длина математического маятника с таким же периодом:

                                                  , , .§

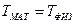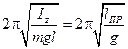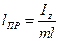Замечание. Как показано в последних двух примерах, уравнения колебаний можно получить, вводя обобщённую координату - угол и обобщённую квазиупругую силу – момент силы тяжести.

Энергия и импульс гармонического осциллятора.

Пусть задан закон движения осциллятора: .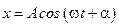

Среднее значение (по времени) некоторой величины  u(t) за интервал времени  (t₁, t₂) – это такое постоянное значение 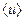, для которого выполняется равенство:

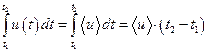                       ,     поэтому .

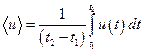Так как колебания незатухающие, то они продолжаются бесконечно долго, поэтому средние значения надо искать на бесконечном интервале:  t₂®+¥.

1) Найдем среднее значение проекции импульса  для колебательного движения:

                              .

    ,

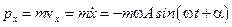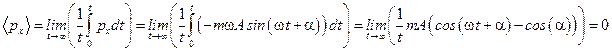 (так 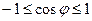   для любых j).

2) Найдём среднее значение кинетической энергии: .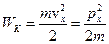

    .

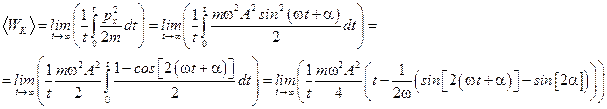Так как 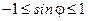   для любых  j,  то .

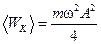3) Найдём среднее значение потенциальной энергии: .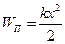

      ,

                                                         .

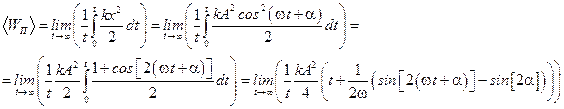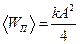С учетом соотношения 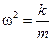  получаем, что .

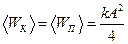4) Найдём среднее значение механической энергии осциллятора:

                                    .

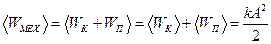Как и следовало ожидать, полная механическая энергия осциллятора остается постоянной.

 

Фазовая плоскость.

Фазовой плоскостью называется двумерное пространство, координатами в котором являются координата точки и проекция импульса (соответственно, обобщённая координата и обобщённый импульс).

Для пружинного маятника из закона сохранения энергии:

                 

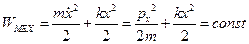
следует, что фазовая траектория точки, совершающей свободные незатухающие колебания, является  эллипсом. Покажем это:

                                        ,   ,

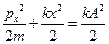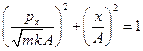где главные полуоси эллипса равны: , .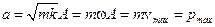

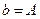Замечание. В случае если система состоит из  N  осцилляторов, то фазовое пространство имеет размерность  2N.

Векторная диаграмма.

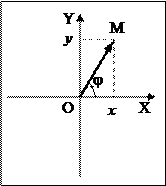Рассмотрим радиус-вектор точки  М, вращающейся вокруг начала координат с постоянной  угловой скоростью  w. Угол между радиус-вектором и осью  Х  меняется с течением времени по закону: 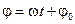, где  j₀ – его начальное значение. Пусть длина радиус-вектора úОМê=А.  Координаты точки М:

                   ,

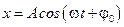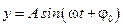
описывают колебания осцилляторов вдоль осей  X  и  Y.

Данная форма представления колебаний называется амплитудной (векторной) диаграммой.

Рассмотрим сложение двух колебаний одного направления: пусть два осциллятора совершают колебания вдоль оси  Х с циклическими частотами  w₁ и  w₂:

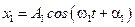                       и .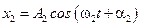

Зададим эти колебания на векторной диаграмме с помощью векторов.

1-е колебание задаётся вектором 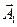, который вращается вокруг начала координат с постоянной угловой скоростью  w₁, угол вращения меняется по закону: .

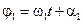2-е колебание задаётся вектором 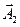, соответственно, угол .

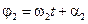Тогда результирующему колебанию 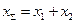  сопоставим вектор  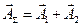 с фазой .

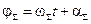      По теореме косинусов:

     .

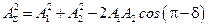Учтем, что ,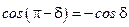

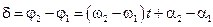      ,  тогда

     ,

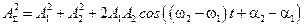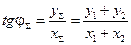       или         .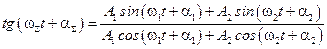

                                             Соответственно, .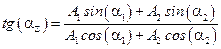

Остановимся подробнее на двух частных случаях.

1) Пусть 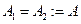, 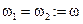. Тогда .

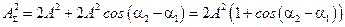Амплитуда результирующего колебания в этом случае не зависит от времени.

Если разность начальных фаз колебаний 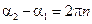, где  n – целое число, то  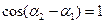  и наблюдается усиление колебаний: .

Если разность начальных фаз колебаний 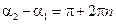, где n – целое число, то  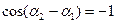   и колебания гасят друг друга: .

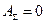Для вывода зависимости результирующего колебания воспользуемся соотношением:

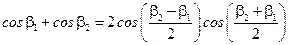, тогда с учётом чётности функции косинуса имеем:

                                 .

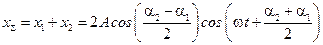Амплитудой должно быть выражение, не зависящее от времени, но амплитуда не может быть отрицательной величиной, следовательно:

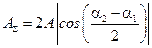                                 ,   тогда

                                 .

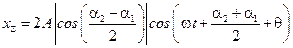Если 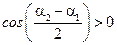,  то 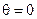,  если  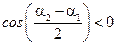 то .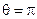

2) Рассмотрим случай, когда амплитуды одинаковые: 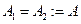, но частоты отличаются на небольшую величину: 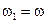, , 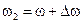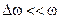. Для упрощения примем, что  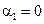и 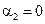. Аналогично предыдущему случаю, получаем:

                                  .

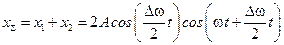Пренебрегая в выражении для фазы второго сомножителя величиной 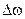 по сравнению с величиной w, получаем:

                                   .

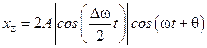Если 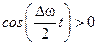,  то 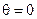, но если 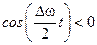,  то .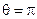

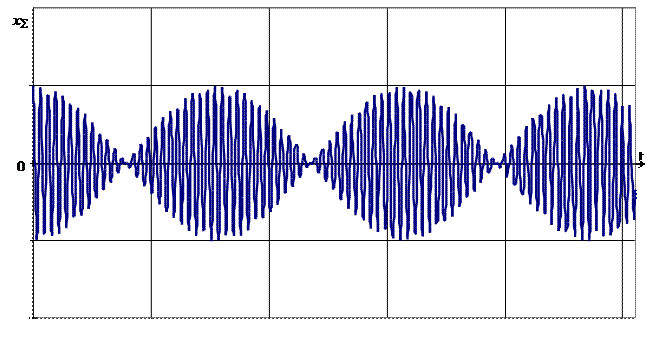
Таким образом, при сложении колебаний близких частот возникает периодическое изменение амплитуды и скачкообразное изменение фазы результирующего колебания – явление, которое называется биением.

---

Дата добавления: 2022-01-22; просмотров: 119; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!