Уравнение с одним неизвестным

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Пусть задана непрерывная функция f(x) и требуется найти все или некоторые корни уравнения

f(x) = 0. (19)

Решение задачи (19) включает несколько этапов:

· оценку количества корней;

· определение их местонахождения;

· получение значений интересующих нас корней с заданной точностью.

Например, если f(x) есть полином n-й степени P_n(x), т.е. нас интересуют корни уравнения

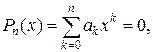(20)

то оно, как известно из курса алгебры, имеет в общем случае n комплексных корней x₁,…,x_n, не обязательно различных. Кроме того, известно их местоположение, они все находятся в круге радиуса 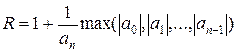, т.е. .

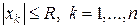Если нас интересуют действительные корни уравнения (19) то полезно составить таблицу значений функций. Если в соседних узлах значения функции имеют противоположные знаки, то на этом интервале существует по крайней мере один корень. Можно также построить график функции y = f(x), корнями уравнения (19) в этом случае являются точки пересечения графика с осью абсцисс.

Заданная точность в оценке значений корней получается путем использования различных итерационных методов. К наиболее эффективным из них относятся:

· дихотомия или деление отрезка пополам;

· метод простых итераций;

· метод Ньютона;

· метод секущих.

Метод дихотомии или деления отрезка пополам состоит в следующем. Пусть найдены две такие точки x₀, x₁, что f(x₀)f(x₁) £ 0, т.е. на отрезке [x₀,x₁] находится не менее одного корня уравнения f(x) = 0. Найдем среднюю точку x₂ = (x₀+x₁)/2 и вычислим f(x₂). Определим, среди пары f(x₀)f(x₂), f(x₂)f(x₁) то произведение, которое не положительно, пусть это будет первое произведение, т.е. f(x₀)f(x₂) £ 0 и искомый корень лежит на отрезке [x₀,x₂], длина которого в два раза меньше предыдущего отрезка. Далее процедура повторяется. Если требуется получить корень с заданной точностью e, то делим отрезок пополам до тех пор, пока его длина не станет меньше 2e, середина этого отрезка и даст значение корня с заданной точностью.

Дихотомия проста и надежна. Процесс сходится к любому простому корню любой непрерывной и не обязательно дифференцируемой функции. Сходимость очень медленная, поскольку для уточнения трех цифр требуется 10 итераций, при этом точность ответа гарантирована.

К недостаткам метода дихотомии относится поиск исходного отрезка, на котором функция меняет знак. Если корней на исходном отрезке несколько, то неизвестно к какому из корней процесс сойдется. Метод не работает для поиска корней четной кратности. Для поиска корней нечетной кратности метод сходится, но он менее точен и плохо устойчив к ошибкам округления. Наконец, метод дихотомии не обобщается на случай поиска корней системы уравнений.

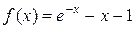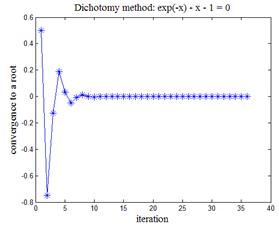
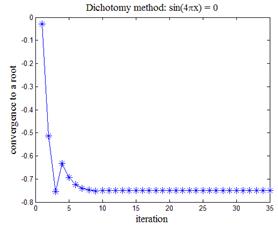
На листинге_№5 приведен код программы поиска корней уравнения (19) методом дихотомии. В качестве тестовых функций взяты две: и 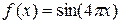. Первая функция имеет один-единственный корень x = 0, вторая функция имеет множество корней x_k = k/4, k = 0,±1,±2,… На рис.6,а приведена динамика сходимости к корню первого уравнения, на рис.6,б — к одному из девяти корней на отрезке [-1,1] второго уравнения.

Листинг_№5

%Программа поиска корней уравнения f(x)=0

%методом дихотомии (деления отрезка пополам)

%очищаем рабочее пространство

clear all

%определяем точность численной оценки корня

eps=1e-10;

%определяем максимальное количество делений

%отрезка пополам (итераций)

itermax=100;

%выбираем различные представления для

%функции f(x), а также исходный отрезак,

%на котором есть хотя бы один корень

% f=@(x)(exp(-x)-x-1);

% x0=-2; x1=3;

f=@(x)sin(4*pi*x);

x0=-1+0.1*randn; x1=1+0.1*randn;

iter=1;

%организуем цикл делений отрезка пополам

%до тех пор, пока либо не достигнута

%нужная точность, либо не превышен предел

%деления отрезка пополам, либо значения

%функции на концах исходного отрезка

%одного знака

while ((x1-x0)>2*eps)&(iter<itermax)&...

(f(x0)*f(x1)<=0)

x2=0.5*(x0+x1);

root(iter)=x2;

if f(x0)*f(x2)<=0

x1=x2;

end

if f(x2)*f(x1)<=0

x0=x2;

end

iter=iter+1;

end

root(iter)=0.5*(x0+x1);

%рисуем историю сходимости итераций к

%корню уравнения

plot(1:iter,root,'-*');


Рис.6,а. Сходимость метода дихотомии к корню уравнения exp(-x) - x - 1 = 0	Рис.6,б. Сходимость метода дихотомии к одному из корней уравнения sin(4p x) = 0

В методе простых итераций исходное уравнение (19) преобразуется к уравнению x = f(x). Процедура преобразования неоднозначна, например, допустимо преобразование вида: x = f(x) = x + y(x)f(x), где y(x) — произвольная непрерывная, отличная от нуля в интересующем нас диапазоне, функция.

Выберем нулевое приближение x₀ и вычислим все последующие приближения по формуле:

x_n₊₁ = f(x_n), n = 0,1,2,… (21)

Очевидно, что, если последовательность x_n, n = 0,1,… сходится к некоторому пределу 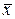, то этот предел является корнем исходного уравнения.

Для изучения условия сходимости процесса (21) предположим, что функция f(x) имеет непрерывную производную, тогда

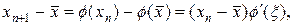(22)

где точка x лежит между x_n и 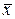. Если всюду 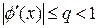, то, согласно (22), следует, что последовательность 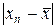, n = 0,1,… убывает не медленнее членов геометрической последовательности со знаменателем q < 1 и последовательность x_n, n = 0,1,… сходится при любом начальном значении x₀. Если 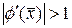, то итерации не сходятся к значению 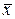, если 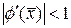, а в отдалении от корня 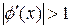, то для сходимости итераций необходимо выбирать начальное приближение из близкой к корню окрестности.

Ясно, что скорость сходимости тем выше, чем меньше значение q. При этом сходимость в окрестности корня определяется величиной 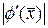и будет особенно высокой при .

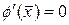Рассмотрим пример решения уравнения f(x) = x² - a, a > 0. Перепишем это уравнение двумя способами:

1) 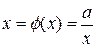и 2) 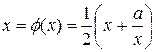. (23)

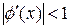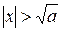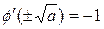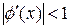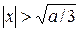Каждый из способов записи (23) порождает соответствующий итерационный процесс. Согласно первой форме записи в (23), при и , т.е. итерационный процесс расходится в окрестности и того и другого корней. Согласно второй форме записи в (23), при и 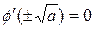, т.е. итерационный процесс сходится при 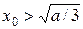к корню 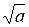и при 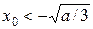к корню .

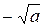Определим критерий сходимости метода простых итераций. Для этого отметим, что в окрестности корня последовательность сходится по закону геометрической прогрессии и можно, согласно (22), записать следующую пару уравнений

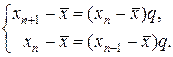(24)

Решая систему уравнений (24) относительно двух неизвестных 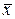и q, найдем оценку точности приближения 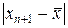, т.е.

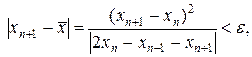(25)

где e — заданное значение точности расчетов. Таким образом, в качестве критерия остановки итерационного процесса выступает условие выполнения неравенства (25).

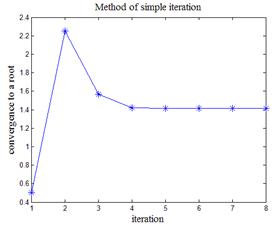
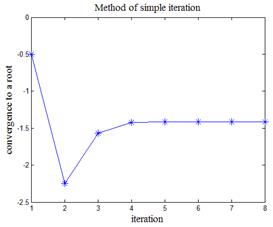
На листинге_№6 приведен код программы численной оценки корня уравнения x² - a = 0 методом простой итерации в форме 2) из (23). На рис.7,а приведена траектория выхода итерационной последовательности на корень 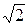, а на рис.7,б — на корень .

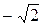Листинг_№6

%Программа поиска корня уравнения

%методом простой итерации

%очищаем рабочее пространство

clear all

%определяем точность численной оценки корня

eps=1e-10;

%определяем максимально возможное число

%итераций

itermax=100;

%определяем параметр уравнения f(x)=x^2-a=0

a=2;

%задаем функцию phi

phi=@(x)0.5*(x+a/x);

%определяем начальное приближение x0

x0=0.5;

x1=phi(x0); x2=phi(x1);

root(1)=x0; root(2)=x1; root(3)=x2;

it=4;

%организуем цикл расчета последовательных итераций

while ((x2-x1)^2/abs(2*x1-x0-x2)>eps)&(it<itermax)

x0=x1; x1=x2; x2=phi(x1);

root(it)=x2;

it=it+1;

end

root(it)=phi(x2);

%рисуем траекторию сходимости итераций к

%корню уравнения

plot(1:it,root,'-*');


Рис.7,а. Сходимость к корню Ö2	Рис.7,б. Сходимость к корню -Ö2

Метод Ньютона называется также методом касательных или методом линеаризации. Запишем следующую последовательность преобразований исходного уравнения (19):

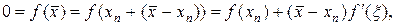
где точка x находится между парой x_n и 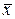, тогда

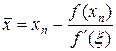. (26)

С помощью (26) можно получить итерационный процесс, если заменить x на x_n и 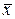на x_n ₊₁. В итоге получаем искомый итерационный процесс, который составляет суть метода Ньютона:

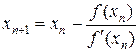. (27)

Геометрический смысл процесса поиска приближенного значения корня (27) представлен на рис.8. Каждая последующая итерация есть пересечения касательной к графику функции y = f(x) в точке предыдущей итерации с осью абсцисс.

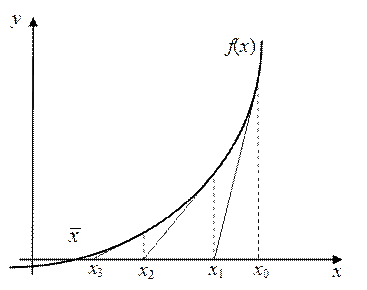
Рис.8. Геометрическая интерпретация к методу Ньютона

Метод Ньютона можно рассматривать как частный случай метода простой итерации, если считать, что 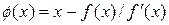, тогда 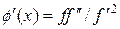. Если 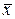p-кратный корень уравнения (19), то в окрестности корня 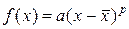, тогда 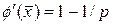, т.е. 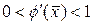. Для простого корня, когда p = 1 имеем .

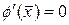Учитывая результаты исследования сходимости последовательности приближений к корню уравнения в методе простой итерации, можно сделать следующие выводы о сходимости итераций в методе Ньютона (27). Если начальное приближение выбрано достаточно близко к значению корня, то итерации Ньютона сходятся, причем скорость сходимости к простому корню велика, а к кратному соответствует скорости геометрической прогрессии. При произвольном нулевом приближении итерации сходятся, когда всюду 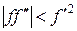. В противном случае итерации сходятся лишь при выборе начального приближения из окрестности корня.

Оценим скорость сходимости метода Ньютона для простого корня. Рассмотрим представление:

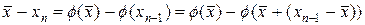
и разложим правую часть в ряд Тейлора по 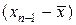, тогда, учитывая равенство 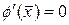, находим

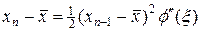, (28)

где .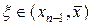

Согласно (28), погрешность текущей итерации пропорциональна квадрату погрешности предыдущей итерации. Для построения критерия точности можно было бы следовать тому же способу, что и в методе простой итерации, т.е. определяем систему уравнений

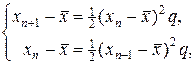
относительно неизвестных 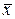и q, решаем ее, после чего оценку точности приближения 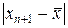выражаем через 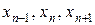. Вводя параметр точности e, определяем критерий сходимости 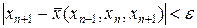. Так как соответствующее выражение довольно громоздко, в качестве критерия можно взять критерий близости соседних итераций, т.е. итерации прекращаются, когда .

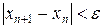Метод Ньютона наиболее часто используется для поиска корней дифференцируемой функции, когда имеется удачное начальное приближение, найденное из каких либо иных соображений.

Сравним скорости сходимости метода простой итерации и метода Ньютона на примере решения уравнения 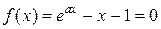. Уравнение имеет очевидный корень 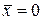. Учитывая вид уравнения, организуем два итерационных процесса для метода простой итерации и метода Ньютона:

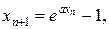(29)

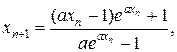(30)

где n = 0,1,… В методе простой итерации сходимость обеспечивается, когда 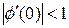, т.е. при .

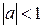На листинге_№7 приведен код программы, которая, согласно (29), (30), рассчитывает последовательные приближения к искомому корню согласно методу простой итерации и методу Ньютона. На рис.9 приведен совместный график, который дает возможность визуально сравнить скорости сходимости для первого и второго методов.

Листинг_№7

%Программа сравнения метода простой итерации

%и метода Ньютона на примере решения

%уравнения exp(ax)-x-1=0

%очищаем рабочее пространство

clear all

%задаем максимальное число итераций

itermax=20;

%определяем параметр уравнения

a=-0.5;

iter=1;

%задаем начальные значения для итераций

%метода простой итерации x0si и для

%метода Ньютона x0n

x0si=3; x0n=3;

rsi(iter)=x0si; rn(iter)=x0n;

%организуем итерационный процесс

while iter<itermax

x1si=exp(a*x0si)-1;

x1n=((a*x0n-1)*exp(a*x0n)+1)/(a*exp(a*x0n)-1);

iter=iter+1;

rsi(iter)=x1si; rn(iter)=x1n;

x0si=x1si; x0n=x1n;

end

%строим графики, иллюстрирующие динамику

%итерационного процесса

plot(1:iter,rsi,'-*',1:iter,rn,'-p');

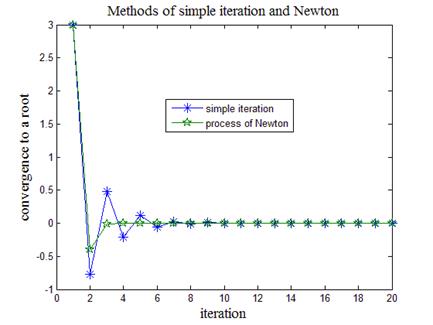
Рис.9. Сравнение скоростей сходимости метода простой
итерации и метода Ньютона

Рассмотрим итерационные процессы высоких порядков. В методе простой итерации выберем функцию f(x) так, чтобы

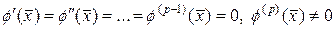. (31)

Итерационный процесс (21) с функцией (31) называется стационарным процессом p -го порядка. Скорость сходимости этого процесса легко можно получить, производя соответствующее разложение Тейлора, т.е.

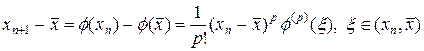. (32)

Если 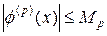, то из (32) следует

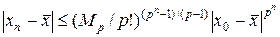Сходимость при p = 1 называют линейной, что соответствует методу простой итерации, при p = 2 — квадратичной, что, например, отвечает методу Ньютона, а при p = 3 — кубичной. Хотя с ростом порядка сходимость усиливается, область гарантированной сходимости уменьшается.

В качестве примера кубической скорости сходимости итераций рассмотрим решение уравнения f(x) = x - x³ = 0, которое естественным образом преобразуется к форме (21), т.е. x = f(x) = x³. Запишем итерационный процесс: 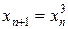, n = 0,1,… Непосредственной проверкой, согласно формуле (32), можно показать, что данный процесс для поиска корня 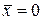является стационарным порядка 3, т.е. имеет место кубическая скорость сходимости.

В отличие от метода Ньютона в методе секущих не требуется вычислять производную исходной функции, что бывает очень важно, когда вычисление производной может быть более проблематичным, чем нахождение значений самой функции. В методе секущих производная, входящая в процесс Ньютона (27), заменяется первой разделенной разностью, которая отыскивается по двум предыдущим итерациям. В итоге имеем следующий итерационный процесс:

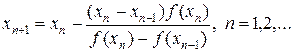(33)

Для работы процесса (33) необходимо задать два начальных значения x₀ и x₁. Процессы, в которых вычисление последующего приближения зависит от двух предыдущих, называют двухшаговыми.

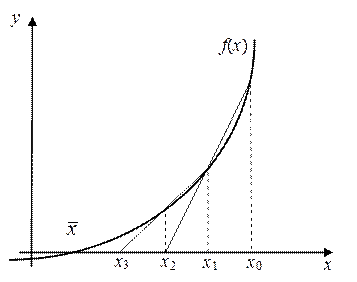
Рис.10. Геометрическая интерпретация к методу секущих

Геометрическая интерпретация метода секущих представлена на рис.10. В отличие от метода Ньютона последующие итерации находятся не из пересечения касательных с осью абсцисс, а соответствующих хорд (секущих).

Оценим скорость сходимости метода секущих. Разложим все функции в (33) в ряд Тейлора с центров в 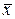. С точностью до бесконечно малых более высокого порядка, находим

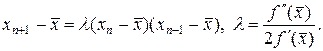(34)

Решение рекуррентного уравнения (34) будем искать в виде, аналогичном (28), (32), т.е. 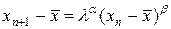. Подставляя это соотношение в (34), находим соотношения для неопределенных параметров:

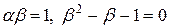. (35)

Только положительный корень квадратного уравнения для b в (35) отвечает условию убывания ошибки, т.е.

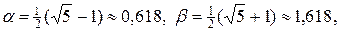
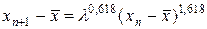. (36)

Оценка (36) для метода секущих является основной. Сравнивая формулы (28) и (36), можно убедиться, что метод секущих сходится медленнее, т.к. для него b = 1,618, а для метода Ньютона — b = 2.

Для сравнения методов секущих и Ньютона обратимся к листингу_№8 программы, где осуществляется численный поиск корня уравнения 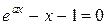. На рис.11 приведен итог работы кода программы. Из рис.11 видно, что методу секущих потребовалось приблизительно в два раза больше итераций (17 против 9) для достижения полной неразличимости двух соседних итераций.

Листинг_№8

%Программа сравнения метода секущих и Ньютона

%очищаем рабочее пространство

clear all

%вводим максимальное количество итераций

itermax=20;

%определяем параметр a уравнения exp(ax)-x-1=0,

%само уравнение и его производную

a=-4;

f=@(x)exp(a*x)-x-1;

df=@(x)a*exp(a*x)-1;

%определяем начальные значения для

%итерационного процесса в методе секущих

x0=1; x1=x0-f(x0)/df(x0);

iters=1;

%организуем итерационный процесс метода секущих,

%где вводится проверка на различимость ближайших

%итераций

while (iters<itermax)&(x0~=x1)

x2=x1-((x1-x0)*f(x1))/(f(x1)-f(x0));

roots(iters)=x2;

iters=iters+1;

x0=x1; x1=x2;

end

iters=iters-1;

%определяем начальное значение для метода Ньютона,

%оно такое же, как и для метода секущих

x0=1;

itern=1;

%организуем итерационный процесс метода Ньютона,

%где вводится проверка на различимость ближайших

%итераций

while (itern<itermax)&(x0~=x0-f(x0)/df(x0))

x1=x0-f(x0)/df(x0);

rootn(itern)=x1;

itern=itern+1;

x0=x1;

end

itern=itern-1;

%строим совместно два графика сходимости к корню

%и для метода секущих, и для метода Ньютона

plot(1:iters,roots,'-*',1:itern,rootn,'-p');

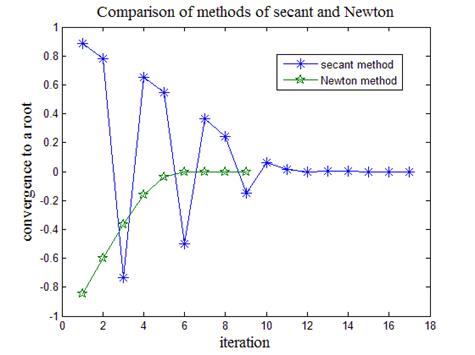
Рис.11. Сравнение скоростей сходимости метода
секущих и Ньютона

Дата добавления: 2022-01-22; просмотров: 31; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!