Работа с разреженными матрицами

Лекция №5

Системы уравнений

Линейные системы уравнений

В линейной алгебре определены четыре основные задачи:

· решение системы линейных уравнений Ax = b, где A — квадратная матрица размером n´n, x, b — вектор-столбцы размером n´1;

· вычисление определителя, детерминанта квадратной матрицы;

· нахождение обратной матрицы;

· определение собственных значений и собственных векторов матрицы (предмет изучения следующей лекции).

Из курса линейной алгебры известно, что линейная система уравнений имеет единственное решение тогда и только, когда определитель системы отличен от нуля. Если же определитель равен нулю, то может оказаться, что система уравнений имеет либо бесконечное количество решений, либо не имеет их вовсе.

На практике помимо существования и единственности решения важна еще устойчивость относительно погрешностей правой части и элементов матрицы. Если представить решение системы уравнений Ax = b в виде x = A^-¹b и проварьировать по правой части и самой матрице, то получим 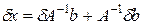. После варьирования уравнения 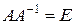и подстановки 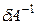в предыдущее уравнение, находим

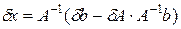. (1)

Согласно (1), поскольку detA ¹ 0 постольку обратная матрица существует и решение системы линейных уравнений устойчиво. Однако если матрица имеет большие значения в своей структуре, то всегда можно подобрать такое возмущение, которой сильно изменит решение, т.е. матрица плохо обусловлена. Плохо обусловленная матрица имеет детерминант близкий к нулю. Близость к нулю детерминанта необходимое, но недостаточное условие плохой обусловленности. Например, пусть задана единичная матрица E размером 100´100. Матрица A = 0,1E имеет детерминант detA = 10^-¹⁰⁰, обратная же матрица вполне хорошего качества A^-¹ = 10E.

В теоретических исследованиях обусловленность часто характеризуют числом обусловленности 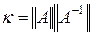, где — некоторая матричная норма. В любой норме k ³ 1. Чем число обусловленности k больше, тем хуже система обусловлена. Система считается плохо обусловленной уже при k » 10³¸10⁴.

Рассмотрим классический пример плохо обусловленной матрицы. Такой матрицей является матрица Гильберта: 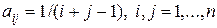. В пакете MATLAB есть специальная функция cond, которая вычисляет число обусловленности k. В таблице ниже приведены значения числа обусловленности k матриц Гильберта для различных значений n — порядка матриц Гильберта. Эти числа получены простой комбинацией операторов: cond(hilb(n)).

Числа обусловленности для матриц Гильберта различных порядков
n =	3	6	9	12	15
k =	524.0568	1.4951e+007	4.9315e+011	1.7945e+016	8.4880e+017

Методы решения линейных систем делят на прямые и итерационные. Прямые методы дают решение за конечное число шагов, они просты и универсальны. Прямые методы обычно используют для матриц порядка n < 10⁴. Итерационные методы часто используют для решения систем со специальными матрицами или слабо заполненными, разреженными матрицами, а также для систем уравнений высокого порядка n =10⁵¸10⁷.

Метод исключения Гаусса

Пусть требуется решить линейную систему уравнений вида:

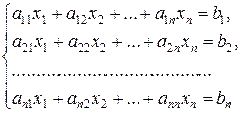(2)

или в другой форме

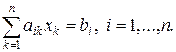(2¢)

В курсе линейной алгебры решения системы уравнений (2) представляются по правилу Крамера в виде отношений соответствующих определителей. Если использовать наиболее оптимальный способ расчета определителя, то по правилу Крамера требуется примерно 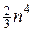арифметических операций. Однако существует более оптимальный способ решения системы уравнений (2) — метод исключения Гаусса, в рамках которого требуется 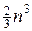арифметических действий.

Начнем исследование системы уравнений (2) с частного случая, когда матрица системы является верхней треугольной, т.е. все ее элементы ниже главной диагонали равны нулю. Выполняя в командном окне MATLAB операцию spy(triu(randn(25))) сгенерируем верхнюю треугольную матрицу и ее графический образ. На рис.1 приведен соответствующий пример верхней треугольной матрицы.

Из последнего уравнения системы с верхней треугольной матрицей находим x_n, подставляя его в предпоследнее уравнение, находим x_n _-₁ и т.д. находим все решение. Общая формула для определения x_k-го имеет вид:

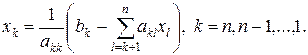(3)

Метод Гаусса выражается в процедуре приведения матрицы системы уравнений к треугольному виду (например, к верхнему треугольному виду рис.1). Это можно сделать следующим образом. Вычтем из второго уравнения первое, умноженное на такое число, чтобы коэффициент при x₁ обратился в нуль, аналогично вычитаем первое уравнение из второго, третьего и т.д. вплоть до n-го. В результате должна получиться новая система уравнений, в которой в первом столбце везде нули, кроме диагонального элемента a₁₁. Затем с помощью второго уравнения путем такой же процедуры обнуляем элементы второго столбца, лежащие ниже главной диагонали. Продолжая эту процедуру для третьего и всех последующих уравнений, преобразуем матрицу системы к верхнему треугольному виду.

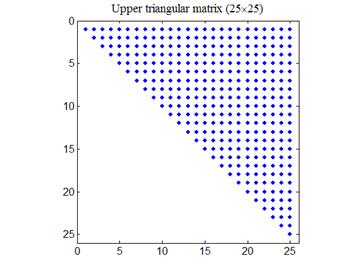
Рис.1. Пример верхней треугольной матрицы
размером 25´25

Пусть проведено исключение элементов из k - 1 столбца. Остальные уравнения с не обнуленными столбцами можно записать в виде:

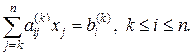(4)

Умножим k-ю строку на число 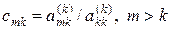и вычтем из m-й строки. Первый ненулевой элемент этой строки обратиться в нуль, а другие элементы можно пересчитать по формулам:

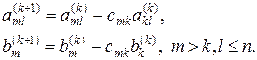(5)

Проведение алгоритма (4), (5) обнуления каждого столбца матрицы ниже главной диагонали заканчивается n - 1-м столбцом, при этом вся процедура называется прямым ходом исключения.

Собирая (4), (5) вместе, будем иметь

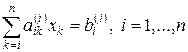
или в развернутой форме

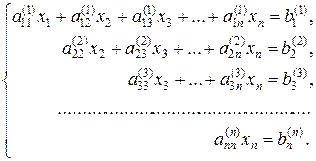(6)

Система уравнений (6) легко решается обратным ходом по формулам (3).

Возможное нарушение в работе алгоритма (4), (5) может быть связано с тем, что на главной диагонали оказался нулевой элемент 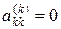. В этом случае необходимо среди строк матрицы ниже k-й найти такую, у которой на k-м месте находится отличный от нуля элемент. Такая строка обязательно должна найтись, если она не находится, то это значит, что в k-м столбце, начиная с k-го номера все элементы нулевые, а значит и детерминант матрицы A равен нулю. Перестановкой строк можно переместить подходящую строку в нужное положение.

Если оказывается, что элемент на главной диагонали 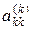мал, то коэффициенты c_mk становятся большими числами и при пересчете элементов матрицы согласно (5) может быть значительная потеря точности на ошибках округления при вычитании больших чисел. Чтобы этого не происходило, среди элементов столбца 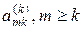находят главный или максимальный и перестановкой строк переводят его на главную диагональ. Этот метод называется методом Гаусса с выбором главного элемента. С выбором главного элемента ошибки округления в методе Гаусса обычно невелики.

Метод Гаусса с выбором главного элемента наиболее прост, надежен и выгоден и по этой причине наиболее востребован при решении линейных систем уравнений с плотно заполненной матрицей порядка n < 10⁴.

Рассмотрим процедуру решения линейной системы уравнений в среде MATLAB. Покажем экспериментально, что в среднем количество операций, осуществляемое центральным процессором при решении линейной системы уравнений, пропорционально кубу порядка матрицы. Покажем, что асимптотически отношение time(n)/n³ стремится к некоторой предстепенной константе при n ® ¥, где time(n) — время работы центрального процессора при данном порядке матрицы n.

На листинге_№1 приведен код соответствующей программы.

Листинг_№1

%Программа изучения затрат времени

%центрального процессора при решении

%систем линейных уравнений

%очищаем рабочее пространство

clear all

%определяем максимальный порядок

%обращаемых матриц

nmax=1000;

k=0;

%организуем цикл решений систем

%уравнений вида Ax=b

for n=1:10:nmax

k=k+1;

order(k)=n;

%формируем случайну матрицу A

%и правую часть b

A=randn(n); b=randn(n,1);

%запоминаем начальный момент времени

%работы центрального процессора

t0=cputime;

%решаем линейную систему уравнений

%Ax=b по формуле: x=A\b

A\b;

%находим последующий момент времени

%вычитаем из него предыдущий и

%делим на куб порядка матрицы

t(k)=(cputime-t0)/n^3;

end

%строим график зависимости предстепенной

%константы от порядка матрицы A

plot(order,t);

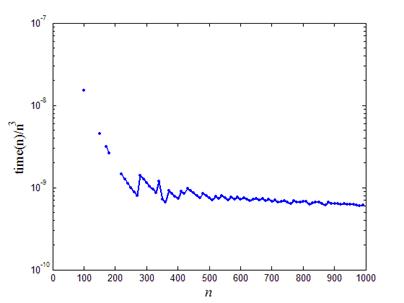
Рис.2. Динамика зависимости предстепенной константы
от порядка матрицы

На рис.2 приведен график зависимости предстепенной константы отношения времени работы центрального процессора к кубу порядка матрицы от порядка матрицы. Видно, что при n ® ¥ действительно отношение time(n)/n³ стремится к некоторой константе, что и подтверждает кубическую зависимость числа операций в методе Гаусса от порядка матрицы.

Определитель и обратная матрица также могут быть найдены методом исключения Гаусса. В процессе исключения Гаусса вычитание строк не меняет определитель, но может измениться его знак при перестановке строк. После приведения матрицы к треугольному виду, можем найти детерминант матрицы в виде произведения ее диагональных элементов:

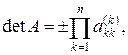(7)

где выбор “+” или “-” зависит от того, четной или нечетной была суммарная перестановка строк.

Процедуру поиска детерминанта матрицы (7) изучим на примере стандартной функции MATLAB — det(A), где A — произвольная матрица n´n. Изучим зависимость величины детерминанта матрицы со случайными элементами, распределенными по нормальному закону со средним 0 и стандартным отклонением 1, в зависимости от порядка матрицы.

На листинге_№2 приведен код соответствующей программы.

Листинг_№2

%Программа изучения процедуры поиска

%детерминанта матрицы, элементы которой

%случайные величины, распределенные по

%нормальному закону со средним 0 и

%стандартным отклонением 1

%очищаем рабочее пространство

clear all

%определяем максимальный порядок

%анализируемых матриц

nmax=300;

k=0;

%организуем цикл поиска детерминанта

%матрицы A – det(A)

for n=1:5:nmax

k=k+1;

order(k)=n;

%формируем случайную матрицу A

A=randn(n);

%вычисляем детерминант матрицы A

d(k)=det(A);

%переходим в логарифмическую шкалу

%при фиксации значений детерминанта

d(k)=sign(d(k))*log10(d(k));

end

%строим график зависимости значений

%детерминанта матрицы от порядка матрицы

plot(order,d);

На рис.3 приведен график зависимости логарифма детерминанта случайной матрицы от порядка матрицы. Видно, что детерминант случайной матрицы экспоненциально растет с ростом порядка матрицы.

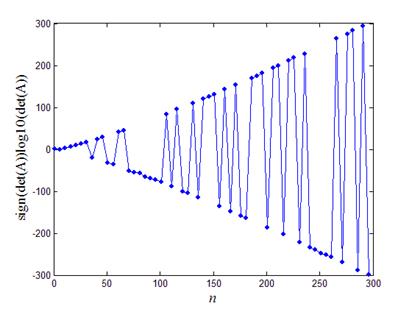
Рис.3. Зависимость детерминанта случайной матрицы от
порядка матрицы

Для вычисления обратной матрицы обозначим ее элементы через 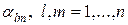и будем исходить из соотношения AA^-¹ = E, тогда верна следующая запись:

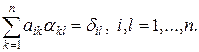(8)

Согласно (8), l-й столбец обратной матрицы можно рассматривать в качестве неизвестного вектора линейной системы уравнений с матрицей A со специальной правой частью. Таким образом, обращение матрицы сводится к решению линейной системы уравнений n раз с одной и той же матрицей, но с разными правыми частями. Приведение системы к треугольному виду осуществляется только один раз, поэтому количество арифметических операций при обращении матрицы лишь в три раза больше, чем при решении системы линейных уравнений, т.е. порядка .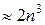

Рассмотрим теперь функцию inv(A) в среде MATLAB, которая возвращает обратную к A матрицу. На листинге_№3 приведен код соответствующей программы.

Листинг_№3

%Программа изучения процедуры поиска

%обратной матрицы, элементы которой

%случайные величины, распределенные по

%нормальному закону со средним 0 и

%стандартным отклонением 1

%очищаем рабочее пространство

clear all

%определяем максимальный порядок

%анализируемых матриц

nmax=1000;

k=0;

%организуем цикл поиска обратной

%матрицы к A - inv(A)

for n=1:5:nmax

k=k+1;

order(k)=n;

%формируем случайну матрицу A

A=randn(n);

%вычисляем обратную к A матрицу

Ainv=inv(A);

%находим ошибку обращения

E=eye(n);

er(k)=norm(A*Ainv-E);

end

%строим график зависимости значений ошибок

%обращения матриц от порядка матриц

plot(order,er);

На рис.4 приведена зависимость ошибки обращения матрицы от ее порядка. Видно, что по мере роста порядка матрицы от 1 до 800 ошибка обращения, выраженная в определенной норме, выросла на пять порядков.

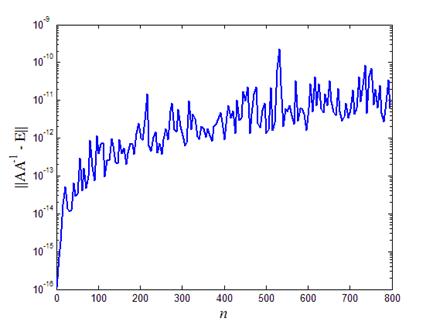
Рис.4. Зависимость ошибки обращения матрицы от ее порядка

Работа с разреженными матрицами

При решении многих прикладных задач возникают разреженные матрицы, т.е. такие матрицы, в которых много нулевых элементов. К числу таких задач относится множество задач математической физики. Например, задача решения одномерного квазилинейного уравнения теплопроводности, рассмотренная в качестве примера в первой лекции, относится к такому классу, т.к. матрица соответствующей линейной системы уравнений является трехдиагональной. Для решения линейных систем с трехдиагональной матрицей разработан специальный метод — метод прогонки, который будет рассмотрен ниже.

На компьютере хранение квадратной матрицы A размером n´n требует n² ячеек памяти и порядка n³ арифметических операций при работе с этой матрицей. Для разреженной матрицы естественно исходить из того, чтобы память, отводимая под хранение разреженной матрицы, была пропорциональна nnz(A), т.е. количеству ненулевых элементов матрицы. Функция nnz(A) в MATLAB возвращает количество ненулевых элементов матрицы. Кроме того, естественно предположить, что и работа с этой матрицей должна требовать количество арифметических операций пропорциональное величине nnz(A). В MATLAB разработан целый набор функций, позволяющий работать с разреженными матрицами, как с обычными.

В листинге_№4 приведена небольшая программа построения пары разреженных матриц: трехдиагональной и случайной симметричной разреженной матрицы. На рис.5 приведен итог работы кода листинга_№4.

Листинг_№4

%Примеры разреженных матриц

n=30;

e=ones(n,1);

%строим трехдиагональную матрицу

A=spdiags([e e e],-1:1,n,n);

subplot(1,2,1);

spy(A);

subplot(1,2,2);

%строим случайную симметричную

%разреженную матрицу

spy(sprandsym(n,0.15));

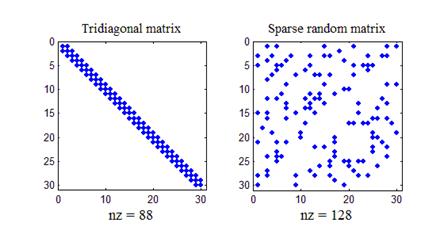
Рис.5. Примеры разреженных матриц

Метод прогонки является частным случаем метода Гаусса и применяется к решению систем с трехдиагональной матрицей. Систему линейных уравнений с трехдиагональной матрицей можно представить в следующем виде:

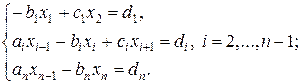(9)

Применение прямого хода процедуры Гаусса к системе (9) сводится к исключению элементов a_i, i = 2,…,n. В результате получается треугольная система, в каждом уравнении которой по два неизвестных x_i и x_i ₊₁. Поэтому формулы обратного хода имеют такой вид:

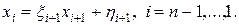(10)

Расчеты обратного хода предполагают знание x_n, которое находится из решения пары уравнени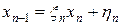й: и 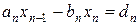. Откуда следует, что

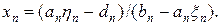(11)

Уменьшим в (10) индекс i на единицу и сделаем подстановку в (9), тогда

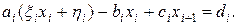(12)

Решая (12) относительно x_i, находим

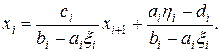(13)

Учитывая условие того, что уравнения (10) и (13) должны совпадать, получаем

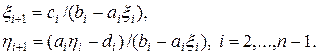(14)

Расчеты прямого хода по формулам (14) предполагают, знание величин x₂ и h₂. Эти величины находятся из сравнения формы (10) при i = 1 и уравнения 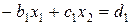, т.е.

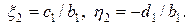(15)

Вычисления по формулам прогонки (9) — (15) требуют 6n ячеек памяти и 10n арифметических операций.

В расчетах прямого хода и при вычислении x_n по формуле (11) может случиться деление на нуль. Сформулируем достаточные условия того, что это не произойдет. Пусть выполнено условие преобладания диагональных элементов, т.е.

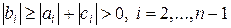(16)

и верны еще два дополнительных условия

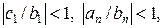(17)

тогда в формулах (11), (14) деление на нуль не произойдет и исходная система (9) будет иметь единственное решение.

Пусть при некотором i величина 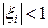, тогда, при условии (16), верна следующая цепочка неравенств:

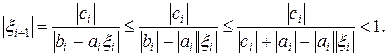(18)

Поскольку, согласно первому условию в (17), 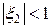постольку, согласно (18), 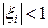для всех i = 2,…,n. Раскрывая последнее неравенство, находим 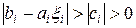, что и требовалось доказать по поводу формул прямого хода. Аналогично с учетом второго условия в (17) доказывается неравенство

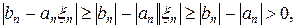
которое гарантирует отсутствие деления на ноль в формуле (11).

Дата добавления: 2022-01-22; просмотров: 141; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!