Структурные средние: мода и медиана
При изучении вариации применяются такие характеристики ряда распределения, которые описывают количественно его структуру, строение. Таковыми являются медиана – величина варьирующего признака, делящая совокупность на две равные части – со значением признака меньше медианы и со значением признака больше медианы. Медиану часто используют как более надежный показатель типичного значения признака, нежели средняя арифметическая, если ряд значений неоднороден, включает резкие отклонения от средней.
Чтобы найти значение медианы необходимо сначала определить медианный номер – 
n – число вариант в вариационном ряду.
Для ранжированного ряда медиана будет определяться как значение признака у единицы совокупности, находящейся в середине ряда. Если в ряду четное число единиц, то медиана определяется как среднее арифметическое между двумя центральными значениями. Для ряда распределения, отражающего процентное распределение признака по группам, или такое распределение, которое может быть переведено в процентное, в качестве медианы принимается значение признака, в котором накопленное процентное соотношение достигает 50%.
В интервальном ряду распределения для нахождения медианы применяется формула:
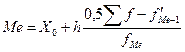, (9.1)
где Ме – медиана;
X0 – нижняя граница интервала, в котором находится медиана;
h – величина (размах) интервала;
– накопленная частота в интервале, предшествующем медианному;
|
|
|
f Me – частота в медианном интервале.
Аналогично медиане вычисляются значения признака, делящие совокупность на 4 равные по численности части – квартили, которые обозначаются заглавной латинской буквой Q с подписным значком номера квартиля. Ясно, что Q 2 совпадает с Ме. Для первого и третьего квартилей приводим формулы:
и 
Значения признака, делящие ряд на 5 равных частей, называются квинтилями, на 10 частей – децилями, на 100 частей – перцентилями. Эти характеристики применяются при необходимости подробного изучения структуры ряда распределения.
Мода - величина признака, которая встречается в изучаемом ряду распределения чаще всего. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если в ряду распределения встречаются 2 или несколько равных (и даже несколько различных, но больших чем соседние) значений признака, то он считается соответственно бимодальным или мультимодальным. Это свидетельствует о неоднородности совокупности, возможно, представляющей собой агрегат нескольких совокупностей с разными модами. В интервальном ряду распределения интервал с наибольшей частотой является модальным. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения (число единиц совокупности, приходящихся на единицу измерения варьирующего признака) достигает максимума. Это условное значение и считается точечной модой. Логично предположить, что такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Моду обычно вычисляют по формуле:
|
|
|
, (9.2)
где Мо – мода;
Х0 – нижнее значение модального интервала;
f Mo – частота в модальном интервале;
f Mo-1 – частота в предыдущем интервале;
f Mo+1 – частота в следующем интервале за модальным;
h – величина интервала.
Показатели вариации
Показатели вариации подразделяются на:
1. Абсолютные: размах вариации; среднее линейное отклонение; среднее квадратическое отклонение; дисперсия.
2. Относительные: коэффициент осцилляции, коэффициент вариации, относительное линейное отклонение.
Простейшим показателем является размах вариации – абсолютная разность между максимальным и минимальным значениями признака из имеющихся в изучаемой совокупности значений:
|
|
|
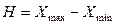. (9.3)
Поскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измерять закономерную силу его вариации во всей совокупности. Показателем силы вариации выступает не арифметическая средняя отклонений, а средний модуль отклонений, или среднее линейное отклонение :
или 
. (9.4)
Простота расчета и интерпретации составляют положительные стороны показателя Л, однако математические свойства модулей «плохие»: их нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением, параметром которого является не средний модуль отклонений, а среднее квадратическое отклонение, обозначаемое малой греческой буквой сигма ( 
) или s и вычисляемое по формуле (9.5) – для ранжированного ряда и по формуле (9.6) – для интервального ряда:
; (9.5) 
. (9.6)
Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего модуля отклонений. Разница между ними тем больше, чем больше в изучаемой совокупности резких, выделяющихся отклонений, что служит индикатором «засоренности» совокупности неоднородными с основной массой элементами. Для нормального закона распределения отношение 
.
|
|
|
Квадрат среднего квадратического отклонения представляет собой дисперсию отклонений, на использовании которой основаны практически все методы математической статистики, ее формула имеет вид (3.7) – для несгруппированных данных (простая дисперсия) и (9.8) – для сгруппированных (взвешенная дисперсия):
; (9.7) 
. (9.8)
Еще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь в ее центральной части, служит среднее квартильное расстояние (отклонение), т.е. средняя величина разности между квартилями, определяемая по формуле (9.9):
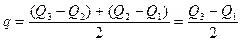. (9.9)
Сила вариации в центральной части совокупности, как правило, меньше, чем в целом по всей совокупности. Соотношение между средним линейным отклонением и средним квартильным расстоянием служит для изучения структуры вариации: большое значение такого соотношения свидетельствует о наличии слабоварьирующего «ядра» и сильно рассеянного вокруг него окружения в изучаемой совокупности.
Если изучаемая совокупность состоит из нескольких групп, образованных на основе какого-либо признака, то помимо общей дисперсии 
определяют также межгрупповую дисперсию 
и внутригрупповую дисперсию 
.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию и находится по формулам (9.7) и (9.8).
Межгрупповая дисперсия 
измеряет вариацию признака под влиянием фактора, положенного в основание группировки: 
, где 
– средняя по отдельной группе; 
– число единиц по отдельной группе.
Средняя внутригрупповая (частная) дисперсия 
измеряет вариацию, возникающую под влиянием других, неучтенных факторов. Это дисперсия не зависит от фактора положенного в основание группировки. Чтобы определить ее, надо исчислить вначале внутригрупповые дисперсии по каждой группе в отдельности, а затем среднюю из них. Внутригрупповые дисперсии определяются по формулам:
– простая;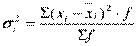 
– взвешенная,
где 
– индивидуальные значения признака внутри отдельной группы.
Средняя внутригрупповая дисперсия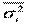 
: 
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий: 
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную, а также судить о силе влияния группировочного признака.
Эмпирический коэффициент детерминации 
показывает долю, обусловленную вариацией группировочного признака, в общей вариации изучаемого признака: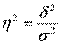 
.
Эмпирическое корреляционное отношение 
показывает влияние признака, положенного в основание группировки, на вариацию результативного признака:
.
Эмпирическое корреляционное отношение варьирует в пределах от 0 до 1. При 
связи нет, при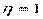 
– связь полная. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям.
Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков необходимы относительные показатели вариации, которые вычисляются как отношение абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака, то есть показатели (9.10) – (9.13):
– относительный размах вариации: 
; (9.10)
– линейный коэффициент вариации: 
; (9.11)
– квадратический коэффициент вариации: 
; (9.12)
– относительное квартильное расстояние: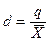 
. (9.13)
Оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава, она состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив.
Различная сила, интенсивность вариации обусловлены объективными причинами, поэтому нельзя говорить о каком-либо универсальном критерии вариации так как для разных явлений и признаков этот критерий различен.
Для дальнейшего изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели называются центральные моменты распределения порядка, соответствующего степени, в которую возводятся отклонения.
Таблица 9.1. Центральные моменты
| Порядок момента | Формула | |
| по не сгруппированным данным | по сгруппированным данным | |
| Первый μ1 | 
| 
|
| Второй μ2 | 
| 
|
| Третий μ3 | 
| 
|
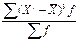
| Четвертый μ4 |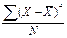 
| 
|
Величина третьего момента μ3 зависит, как и его знак, от преобладания положительных кубов отклонений над отрицательными кубами либо наоборот. При нормальном и любом другом строго симметричном распределении сумма положительных кубов строго равна сумме отрицательных кубов, поэтому на основе третьего момента строится показатель, характеризующий степень асимметричности распределения – коэффициент асимметрии:
. (9.14)
Симметричная кривая отображает равномерное распределение изучаемой совокупности. Асимметричная кривая показывает, что большая часть единиц обладает значениями признака (вероятностями появления) большими (правосторонняя, рис.9.3.а) или меньшими (левосторонняя, рис.9.3.б), чем значение средней величины:
Рис. 9.3. Асимметричная кривая распределения
Английский статистик К.Пирсон на основе разности между средней арифметической величиной и модой предложил другой показатель асимметрии :
. (9.15)
Показатель асимметрии Пирсона (3.15) зависит от степени асимметричности в средней части ряда распределения, а показатель асимметрии (3.14) – от крайних значений признака.
С помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения – эксцесс (от англ. «излишество»). Показатель эксцесса рассчитывается по формуле:
. (9.16)
Чаще всего эксцесс интерпретируется как «крутизна» распределения, что не совсем верно. График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Не говоря уже о том, что, изменяя масштабы по осям абсцисс и ординат, любое распределение можно искусственно сделать «крутым» и «пологим». Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной σ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Такое сравнение изображено на рис. 9.3.
|
|
|
Рис. 9.3. Эксцесс распределения
Наличие положительного эксцесса означает наличие слабо варьирующего «ядра» и сильно рассеянного вокруг него окружения в изучаемой совокупности. Отрицательный эксцесс означает отсутствие такого «ядра».
По значениям показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному: показатели асимметрии и эксцесса не должны превышать своих двукратных средних квадратических отклонений, т.е. 
и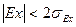 
. Эти средние квадратические отклонения вычисляются по формулам (9.17) и (9.18):
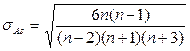; (9.17) 
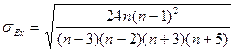. (9.18)
Рассмотрим процедуру анализа вариации сгруппированных данных на примере.
Пример. В группе из 15 студентов проведено практическое занятие, на котором различные студенты решили разное количество задач. Необходимо определить, зависит ли число решенных студентом задач от того, подготовился он к занятию или нет.
Таблица 9.2. Группировка студентов по признаку "подготовка к занятию"
| Группа | Число студентов | Количество решенных задач | Групповая средняя |
| Подготовленные | 10 | 10; 9; 8; 9; 9; 8; 9; 8; 9; 9. | 8,8 |
| Неподготовленные | 5 | 6; 5; 4; 6; 5. | 5,2 |
| Итого | 15 | 7,6 |
Найдем общую, внутригрупповые, среднюю дисперсию из внутригрупповых и межгрупповую дисперсии.
Величина общей дисперсии характеризует различие оценок по всем 15 студентам и рассчитывается следующим образом:
.
Внутригрупповая дисперсия – это мера отклонения значений признака отдельных единиц в группе от среднего по данной группе значения признака. Внутригрупповая дисперсия определяет меру рассеивания значений признака по единицам одной группы под лиянием всех факторов, кроме фактора, положенного в основу группировки.
В рассматриваемом примере в основу группировки положен признак подготовленности к
занятию. Следовательно, внутригрупповая дисперсия в каждой группе характеризует
расхождение в числе решенных задач, не связанное с фактом подготовленности к занятию (индивидуальные способности, «списал решение у соседа», случайные факторы и т.п.):
Средняя дисперсия из внутригрупповых определяет меру рассеивания значений признака по всем единицам совокупности под влиянием всех факторов, кроме фактора, положенного в основу группировки и рассчитывается как средняя из внутригрупповых дисперсий.
В примере средняя дисперсия из внутригрупповых (остаточных) определяет меру рассеивания значений признака (числа решенных задач) по всем единицам совокупности (по 15 студентам) под влиянием всех факторов, кроме фактора, положенного в основу группировки (кроме фактора подготовленности к занятию):
В данном случае средняя дисперсия из остаточных рассчитывается как средняя взвешенная по правилу расчета средних для относительных показателей. Весом выбирается число студентов в группе, т.к. именно эта величина является знаменателем при расчете средних дисперсий в группах.
Межгрупповая дисперсия – это мера отклонения средних в группе значений
признака от общей по совокупности средней величины значения признака.
Межгрупповая дисперсия определяет меру рассеивания значений признака под
влиянием фактора, положенного в основу группировки, измеряя вариацию
значений групповых средних.
В примере 
Проверим правильность выполненного расчета: 3,31=0,43+2,88 -
– правило выполняется, следовательно, расчет выполнен правильно.
Найдем коэффициентом детерминации: 
В рассмотренном примере количество решенных студентами задач на 87 %
обусловлено их готовностью к занятию и только на 13 % другими факторами.
Зависимость считается существенной, если коэффициент детерминации
превышает 50 %.
ГЛОССАРИЙ
Дискретный ряд – статистическая таблица, состоящая из двух строк или граф, в одной из которых представлены значения признака (xj), а в другой – количество единиц совокупности с данным значением признака или частота появления признака, (fj);
Интервальный ряд – статистическая таблица, состоящая из двух строк или граф, в одной из которых представлены интервалы значения признака (xj), а в другой – частота появления признака, (fj).
Медиана – это значение признака, делящее ряд на две равные части, со значениями признака, соответственно, меньше и больше медианы.
Медианный интервал – это первый интервал значений признака, в котором
накопленная частота появления признака превышает половину объема совокупности.
Межгрупповая дисперсия – это мера отклонения средних в группе значений признака от общей по совокупности средней величины значения признака.
Многомерная средняя величина – это обобщенная характеристика некоторого явления, построенная на основе сведения в единый показатель частных его характеристик.
Мода – это наиболее часто встречающееся значение признака.
Модальный интервал – это интервал значений признака, в котором частота появления признака максимальная в ряду.
Общая дисперсия – это мера отклонения значений признака отдельных ЕСС от среднего по совокупности значения признака.
Остаточная (внутригрупповая) дисперсия – это мера отклонения значений признака отдельных ЕСС в группе от среднего по данной группе значения признака.
Ранжированный ряд – перечень единиц статистической совокупности и
соответствующих им значений признака в порядке его убывания или возрастания;
Средняя арифметическая величина – это такая средняя, которая сохраняет сумму
значений признака при замене индивидуальных значений на средние.
Средняя величина – количественная характеристика общего в явлениях и процессах, рактеристика статистической закономерности.
Средняя гармоническая величина – это такая средняя, которая сохраняет неизменной
сумму значений, обратных значениям признака при замене индивидуальных значений на средние.
Средняя геометрическая величина – это такая средняя, которая сохраняет неизменным произведение значений признака при замене индивидуальных значений на средние.
Средняя квадратическая величина – это такая средняя, которая сохраняет неизменной сумму квадратов значений признака при замене индивидуальных значений на средние.
Средняя кубическая величина – это такая средняя, которая сохраняет неизменной сумму кубов значений признака при замене индивидуальных значений на средние.
Вопросы для обсуждения.
1. Что представляет собой вариация признака, от чего зависят ее размеры?
2. Что такое размах вариации, по какой формуле он исчисляется, в чем его недостаток как показателя вариации?
3. Что представляет собой среднее линейное отклонение, его формулы; в чем его недостаток как показателя вариации?
4. Какой показатель вариации называется дисперсией? По какой формуле она рассчитывается?
5. Что называется среднеквадратическим отклонением? По каким формулам оно вычисляется?
6. Коэффициент вариации как показатель, формула его вычисления и значение для экономического анализа.
7. Что характеризует межгрупповая дисперсия, ее формула расчета?
8. Как определяются внутригрупповые дисперсии, средняя их внутригрупповых дисперсий, их формулы?
9. Что представляет правило сложения дисперсий, в чем его практическое значение?
10. Что называется эмпирическим коэффициентом детерминации, каков его смысл?
11. Что называется эмпирическим корреляционным отношением, в чем его смысл?
12. Как определяются мода и медиана в дискретных и интервальных вариационных рядах?
13. Коэффициент асимметрии и его назначение.
14. Эксцесс и его назначение.
Дата добавления: 2022-01-22; просмотров: 23; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!