Определители и их свойства. Вычисление определителей
ЛИНЕЙНАЯ АЛГЕБРА
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Матрицы и операции над ними
Матрицей называется прямоугольная таблица из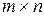 
(“эм на эн”) элементов 
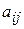некоторого множества: 
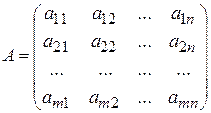. (1)
Числа, из которых составлена матрица, называются элементами матрицы.
Сокращенно матрица обозначается как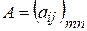 
( 
, 
).
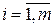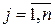Запись 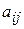означает элемент матрицы, стоящий в 
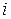- й (“итой”) строке ( 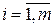) и в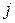 
- м (“житом”) столбце ( ).
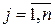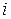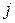В этом случае числа и называются индексами элемента, и они обозначают положение этого элемента в матрице. Первый индекс элемента матрицы указывает номер строки, второй – номер столбца.
Величина 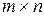называется размерностью матрицы.
Матрица вида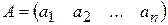 
называется матрицей-строкой или просто строкой.
Матрица вида 
называется матрицей-столбцом или просто столбцом.
Если в матрице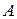 
одна строка и один столбец ( 
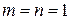), то она считается одноэлементной (представлена одним числом).
Если число строк и столбцов совпадают (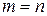 
), то матрица называется квадратной n -го (“энного”) порядка: 
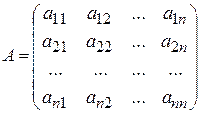. (2)
У квадратной матрицы есть две диагонали.
Элементы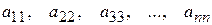 
образуют главную диагональ, а элементы 
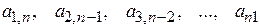- побочную диагональ.
Пример 1.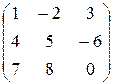 
- квадратная матрица 3-го порядка, 
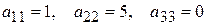- главная диагональ, 
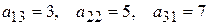- побочная диагональ.
Квадратная матрица (2) называется диагональной, если все элементы, не лежащие на главной диагонали, равны нулю: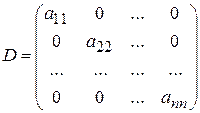 
. (3)
Пример 2.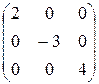 
- диагональная матрица.
Единичной называется диагональная матрица, все диагональные элементы которой равны единице (обозначается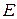 
): 
.
|
|
|
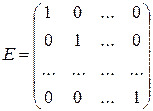Если в матрице все элементы равны нулю, то такая матрица называется нулевой, или нуль-матрицей и обозначается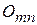 
.
Две матрицы одинакового размера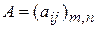 
и 
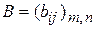называются равными ( 
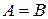), если равны их соответствующие элементы, то есть 
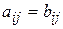для всех значени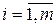й 
и .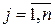
Если в матрице 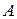поменять местами строки и столбцы (или для каждого элемента поменять местами индексы 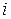и 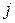), то полученная матрица называется транспонированной и обозначается 
.
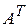Пример 3.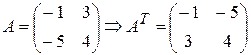 
.
Матрица 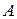называется симметрической, если она не меняется при транспонировании, то есть 
.
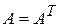Над матрицами можно выполнять следующие операции: сложение и вычитание матриц, умножение матрицы на число, умножение матриц.
Суммой двух матриц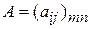 
и 
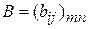называется матрица 
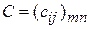такая, что 
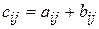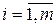, где и .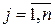
Обозначение: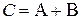 
.
Замечание 1. Сумма и разность существуют только для матриц одинакового размера.
Свойства операции сложения матриц:
1) 
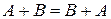(коммутативность сложения);
2) 
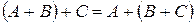(ассоциативность сложения);
3) если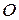 
– нулевая матрица того же порядка, что и матрица 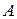, то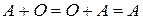 
(нейтральный элемент относительно сложения).
Пример 4.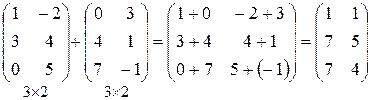 
.
Аналогично определяется разность двух матриц: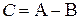 
, где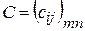 
, 
, 
.
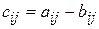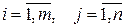Произведением матрицы 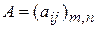на число 
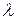(лямбда) называется матрица 
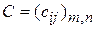такая, что 
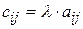, где , .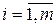
|
|
|
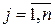Обозначение: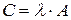 
.
Свойства операции умножения матрицы на число:
1) 
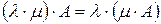(мю);
2) 
;
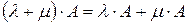3) 
;
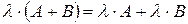4) 
;
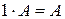5) 
;
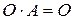6) 
.
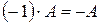Пример 5.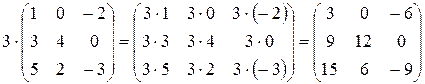 
.
Произведением матрицы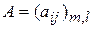 
на матрицу 
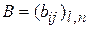называется матрица 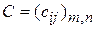, каждый элемент которой 
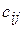равен сумме произведений элементов 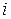-той строки матрицы 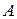на соответствующие элементы 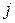-го столбца матрицы 
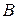, то есть 
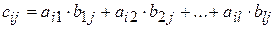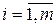, где и .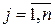
Обозначение: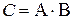 
.
Замечание 2. Умножение допустимо, если число столбцов матрицы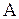 
равно числу строк матрицы 
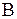. При этом число строк матрицы 
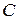будет равно числу строк матрицы 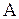, а число столбцов матрицы 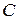будет равно числу строк матрицы .
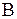Свойства операции умножения матриц:
1) 
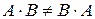(в общем случае операция не коммутативна);
2) 
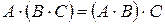(ассоциативность);
3) 
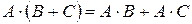(дистрибутивность);
4) 
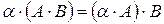(альфа);
5) 
.
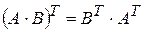Пример 6.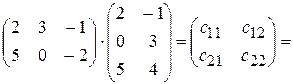 
.
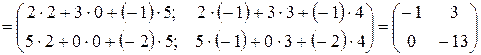Если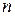 
- целое неотрицательное число, тогда 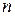-й степенью квадратной матрицы 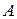называется матрица, которая вычисляется следующим образом: 
; 
; 
.
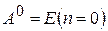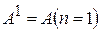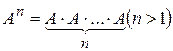Определители и их свойства. Вычисление определителей
Понятие определителя вводится только для квадратных матриц.
Каждой квадратной матрице 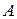порядка 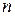ставится в соответствие по определенному закону некоторое число, называемое определителем (детерминантом) матрицы 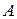или просто определителем 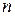-го порядка.
|
|
|
Обозначения: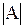 
, 
, 
.
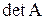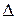Определитель матрицы 1-го порядка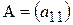 
определяется как 
.
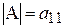Пример 1.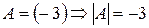 
.
Определитель матрицы 2-го порядка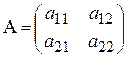 
вычисляется по формуле: 
.
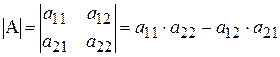Пример 2.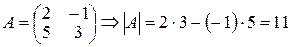 
.
Определитель матрицы 3-го порядка вычисляется по формуле:
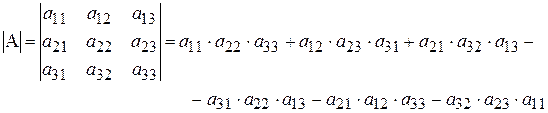
Эта формула легко запомнить, если представить ее в виде схемы:
“+” “-”
Схема вычисления определителей третьего порядка называется правилом треугольников или правилом Саррюса.
Пример 3.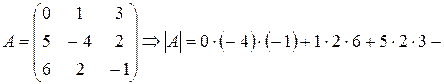 
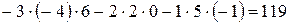
Пусть дан определитель 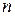-го порядка 
.
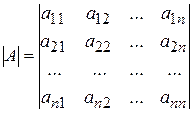Минором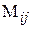 
элемента 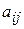определителя n-го порядка называется определитель (n-1)-го порядка (“эн минус первого”), полученный из данного определителя вычеркиванием i-й строки и j-го столбца.
Пример 4.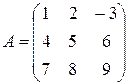 
.
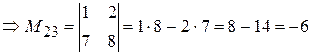Алгебраическим дополнением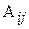 
элемента 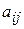определителя n-го порядка называется его минор, взятый со знаком 
: = .
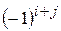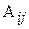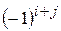
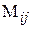Пример 5.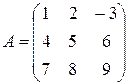 
.
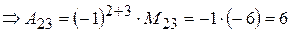Теорема (Лапласа). Определитель матрицы n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
, 
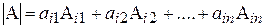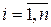- разложение определителя по строке;
, 
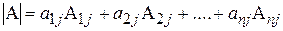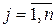- разложение определителя по столбцу.
|
|
|
Пример 6. Вычислить определитель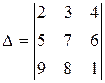 
.
Решение.Вычислим данный определитель разложением по элементам первой строки: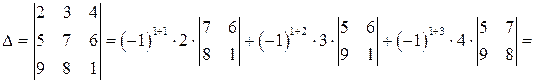 
.
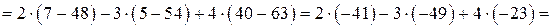
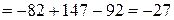Вычисления по теореме Лапласа становятся очень простыми, если в i-той строке или j-м столбце определителя все элементы кроме одного равны нулю.
В этом случае вычисление определителя n-го порядка сводится к вычислению 1-го определителя (n-1)-го порядка.
Преобразование определителей к нужному виду, а также их вычисление выполняется на основе свойств определителей.
Свойства определителей .
1.Определитель не меняется при транспонировании матрицы.
2.Если одна из строк (один из столбцов) определителя состоит из нулей, то определитель равен нулю.
3.Определитель, содержащий две одинаковые строки (столбца), равен нулю.
4.Определитель, содержащий две пропорциональные строки (столбца), равен нулю.
5.При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
6.Общий множитель элементов любой строки (столбца) можно вынести за знак определителя.
7.Величина определителя не изменится, если к одной из его строк (столбцов) прибавить другую строку (столбец), умноженную на какое угодно число.
Пример 7. Вычислить определитель .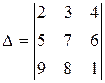
Решение.
Вычислим этот определитель, разложив его по элементам третьего столбца.
Для того чтобы упростить вычисления сделаем следующие преобразования: умножим третью строку на “-6” и прибавим ее ко второй строке (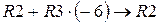 
); умножим третью строку на “-4” и прибавим ее к первой строке ( 
):
.
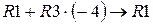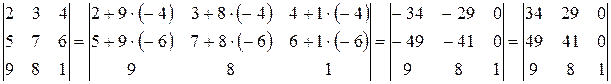Разложим определитель по элементам третьего столбца:
.
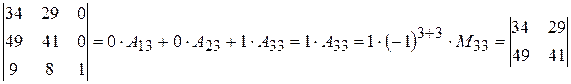Вычтем второй столбец из первого столбца (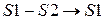 
):
.
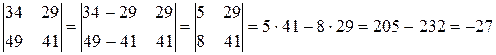Обратная матрица
Квадратная матрица 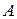называется невырожденной, если её определитель отличен от нуля: 
.
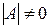Для квадратной невырожденной матрицы 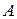существует обратная матрица, которую обозначают 
.
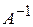Матрица 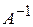называется обратной для матрицы 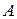, если выполняется соотношение 
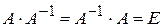(*), где 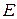единичная матрица одного порядка с матрицей .
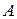Дата добавления: 2022-01-22; просмотров: 21; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!