Нестаціонарні випадкові процеси

Лекція 6

РОЗДІЛ 4 Аналіз випадкових сигналів

Тема 6. Характеристики випадкових сигналів. Аналіз випадкових сигналів

 

1. Характеристики випадкових сигналів

Визначення випадкового сигналу. Моделі випадкових сигналів (процесів). Імовірнісні характеристики випадкових процесів. Числові характеристики випадкових процесів. Приклади імовірнісних розподілів.

2. Аналіз випадкових сигналів

Кореляційні функції випадкових сигналів (процесів). Стаціонарні та ергодичні випадкові процеси. Спектральні характеристики. Теорема Вінера-Хинчина. Ефективна ширина спектра. Білий шум.

 

1. Характеристики випадкових сигналів

Випадкові сигнали

На відміну від детермінованих сигналів, форму яких відома, миттєві значення випадкових сигналів заздалегідь не відомі і можуть бути передбачені лише з деякою ймовірністю, яка менша за одиницю. Характеристики таких сигналів є статистичними, тобто мають імовірнісний вигляд. У радіотехніці існує два основні класи сигналів, що потребують імовірнісного опису. По-перше, це шуми - електромагнітні коливання, що хаотично змінюються в часі, виникають в різноманітних фізичних системах із-за безладного руху носіїв заряду. По-друге, випадковими є усі сигнали, що несуть інформацію, тому для опису закономірностей, властивих осмисленим повідомленням, також удаються до ймовірнісних моделей.

Ансамбль реалізацій

Математична модель випадкового сигналу, що змінюється в часі, називається випадковим процесом. За визначенням, випадковий процес Х(t)={x _k(t)} - це функція особливого виду, яка характеризується тим, що її значення у будь-який момент часу t є випадковими величинами.

ЗАУВАЖЕННЯ. У технічній літературі терміни "випадковий сигнал" і "випадковий процес" часто використовуються як синоніми. 

До реєстрації (до прийому) випадковий сигнал слід розглядати саме як випадковий процес, що є сукупністю (ансамбль) функцій часу {x _k(t)} що підкоряються деякій загальній для них статистичній закономірності. Одна з цих функцій x _k(t), що стала повністю відомою після прийому повідомлення, називається реалізацією випадкового процесу. Ця реалізація є вже не випадковою, а детермінованою функцією часу. На рис. 6.1 наведений приклад декількох реалізацій випадкового процесу.

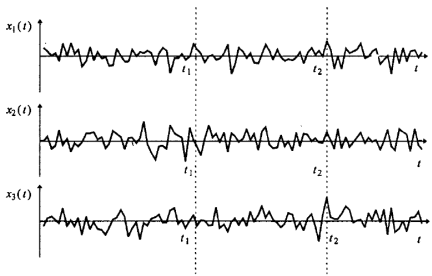
Рис. 6.1. Реалізації випадкового процесу

 

Моделі випадкових процесів

Для аналізу властивостей і характеристик випадкового процесу, а також різних його перетворень необхідно задати математичну модель випадкового процесу. Така модель може бути описом можливих реалізацій випадкового процесу у поєднанні з вказівкою відносної частоти їх появи. Наведемо декілька прикладів моделей випадкових процесів, що задаються таким чином.

Гармонійний сигнал з випадковою початковою фазою

У багатьох практичних задачах використовується модель випадкового процесу, реалізації якого є гармонійними коливаннями з відомою (детермінованими) амплітудою і частотою, але випадковою початковою фазою. Таким чином, реалізація даного випадкового процесу може бути записана як

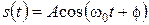
де А - амплітуда (детермінована), ω₀ - частота (детермінована) і φ - випадкова початкова фаза, яка в більшості практично цікавих випадків може вважатися рівномірно розподіленою на інтервалі 0...2π, тобто ймовірності, що має наступну густину:

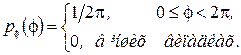
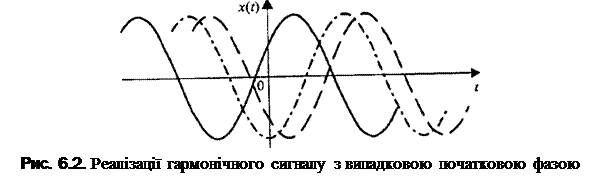
Графіки декількох реалізацій цього випадкового процесу, синусоїди, що зміщені один відносно одного по часовій осі, показані на рис. 6.2.

Як бачите, конкретний вид реалізації процесу в даному випадку визначається значенням усього лише однієї випадкової величини - початкової фази.

ЗАУВАЖЕННЯ

Випадкові процеси, конкретний вид реалізацій яких визначається значеннями кінцевого числа параметрів (випадкових величин), іноді називають квазідетермінованими випадковими процесами.

Імовірнісні характеристики випадкових процесів

Нехай X(t) - випадковий процес, заданий ансамблем реалізацій {x₁(t), x₂(t),..., x_k(t),...}. Вибравши довільний момент часу t₁, зафіксуємо значення, що приймаються усіма реалізаціями: {x₁(t₁), x₂(t₁),..., x_k(t₁),...} (див. рис. 6.1). Сукупність цих значень утворює одновимірний переріз випадкового процесу і є випадковою величиною X(t₁). Нагадаємо коротко основні характеристики випадкових величин, відмітивши при цьому, що для одновимірних перерізів випадкових процесів вони в загальному випадку залежать від обраного моменту часу t₁.

 

Функціональні характеристики

Функція розподілу ймовірності (cumulative distribution function, CDF), що позначається як F(x, t₁), дорівнює ймвірності того, що у момент часу t₁ значення випадкового процесу не перевершує х:

F(x,t₁) = P(X(t₁) 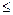x).

F(x,t₁) є неубутною функцією, значення якої лежать в діапазоні 0 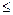F(x,t₁) 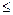1. Для граничних значень х виконуються наступні співвідношення: F(-∞,t₁) 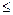0 і F(∞,t₁)=1.

Імовірність потрапляння значення випадкового процесу в інтервал (а, b) дорівнює різниці значень функції розподілу на кінцях цього інтервалу :

Р(а< X(t₁) 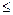b) = F(b,t₁)-F(а,t₁).

Одновимірна густина ймовірності (probability density function, PDF) позначається p(x,t₁) і є похідною від функції розподілу:

p(x,t₁) =dF(x,t₁)/dx.

Добуток p(x,t₁)dx дорівнює ймовірності попадання значення випадкового процесу X(t₁) в нескінченно малий інтервал шириною dx в околиці х:

p(x,t₁)dx = Р(х – dx/2 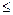 X(t₁) 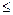х + dx/2),

звідки витікає, що густина ймовірності є невід’ємною функцією: p(x,t₁) 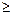0. Щоб розрахувати ймовірність попадання значення X(t₁) у довільний інтервал [а, b], необхідно обчислити наступний інтеграл:

.

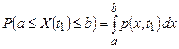Оскільки випадкова величина обов’язково набуває якого-небудь значення, повинна виконуватися умова нормування:

.

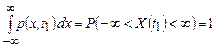Знаючи густину ймовірності, можна розрахувати і функцію розподілу:   

 

.

 

 

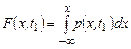Числові характеристики

Знання одновимірної густини ймовірності p(x,t₁) дозволяє здійснити статистичне усереднення як самої величини X(t₁), так і будь-якої функції від неї. Під статистичним усереднюванням (ensemble averaging) мається на увазі усреднення по множині (по ансамблю реалізацій) в якому-небудь перерізі процесу, тобто у фіксований момент часу.

Для практичних застосувань найбільше значення мають наступні параметри випадкового процесу:

□ математичне сподівання (mean value) – це теоретична оцінка середнього зваженого значення випадкового процесу у момент часу t:

                                   m_x(t) = M{X(t)}= 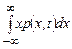.                      (6.1)

ЗАУВАЖЕННЯ

У багатьох практичних завданнях доводиться обчислювати математичне сподівання деякої функції f від випадкової величини x, що має густину ймовірності р_х(х). Таке обчислення виконується по наступній нескладній формулі:

M{f(x)}= 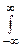f(x)p_x(x)dx.

Формула для математичного сподівання (6.1) є одиничним випадком при f(x)=х.

□ дисперсія (variance), що характеризує середню потужність відхилень випадкового процесу від його середнього значення m_x(t), званих флуктуаціями (fluctuation):

D_x(t) = M{[X(t)-m_x(t)]²} =М{Х²(t)}-m_x²(t)= 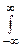x²p(x,t)dx-m_x²(t); (6.2)

□ середнє квадратичне відхилення (standard deviation), що є квадратним коренем з дисперсії і служить амплітудною мірою розкиду значень випадкового процесу в момент часу t відносно математичного сподівання:

.

 

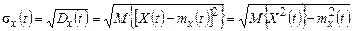ЗАУВАЖЕННЯ

Дисперсія випадкової величини X часто позначається як .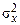

 

Рівномірний розподіл     

Одним з часто використовуваних на практиці законів розподілу випадкових величин є рівномірний розподіл (uniform distribution). При цьому густина ймовірності є константою на деякому інтервалі [а, b] (рис. 6.3, ліворуч). Величина цієї константи, згідно з умовою нормування, має дорівнювати 1/(b - а):

Функція розподілу, згідно 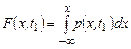, на інтервалі [а, b] лінійно зростає від 0 до 1 (див. рис. 6.3, праворуч):

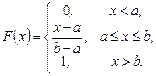
Математичне сподівання, як і передбачає інтуїція, дорівнює середині інтервалу можливих значень випадкової величини:

.

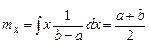ЗАУВАЖЕННЯ. Якщо функція густини ймовірності має симетричний вигляд, то значення математичного сподівання завжди співпадає з центром симетрії.

Для розрахунку дисперсії необхідно спочатку визначити середній квадрат:

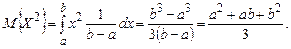
Тепер можна розрахувати дисперсію згідно (1.33) :

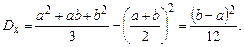
Отже дисперсія дорівнює одній дванадцятій квадрата ширини інтервалу. Середнє квадратичне значення, природно, виявляється пропорційним цій ширині:

 

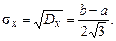
Нормальний розподіл

Нормальний (гаусівський) закон розподілу випадкових величин (normal distribution, Gaussian distribution) дуже зручний для аналізу і часто зустрічається на практиці, особливо він характерний для завад в каналах зв'язку й радіолокації. Одновимірна густина ймовірності нормальної випадкової величини визначається виразом

,

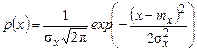де т_х і 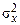 - відповідно математичне сподівання і дисперсія процесу. На рис. 6.3 приведений графік густини ймовірності нормальної випадкової величини, побудований згідно цього виразу при т_х=0 і 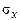= 1.

 

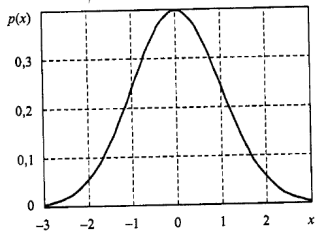
Рис. 6.3. Густина ймовірності випадкової величини з нормальним розподілом

 

Функція розподілу для закону Гауса не виражається через елементарні функції. У вітчизняній літературі прийнято виражати її через так званий інтеграл ймовірності:

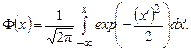
Для нормального закона с математическим ожиданием т_х и дисперсией 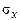 функция распределения выражается через интеграл вероятности следующим образом:

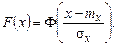
У зарубіжній літературі більшого поширення набула так звана функція помилок (error function) erf:

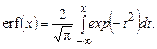
Зв'язок між функцією помилок і інтегралом ймовірності виражається за допомогою лінійних перетворень аргументів функцій і їх результатів:

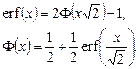
Функція розподілу для нормального закону з математичним сподіванням т_х і дисперсією 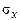 виражається через функцію помилок таким чином:

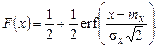
ЗАУВАЖЕННЯ ----------------------------------------------------------------------------------------

У MATLAB, MATHCAD є функції, що реалізовують формулу erf і їй зворотну.

Безпосередньо обчислювати функціональні характеристики нормального закону розподілу можна за допомогою функцій normpdf (густина ймовірності), normcdf (функція розподілу) і norminv (зворотна функція розподілу), Statistics, що входять в пакет.

Широке поширення нормального закону розподілу в природі пояснюється тим, що при підсумовуванні досить великого числа рівнопотужних статистично незалежних випадкових величин, що мають довільну густину розподілу ймовірності, густина розподілу суми прямує до нормальної. Це положення носить назву центральної граничної теореми. Дуже корисною для математичного аналізу властивістю нормального розподілу є те, що з некорельованості випадкових гаусівських величин виходить їх статистична незалежність (про різницю між цими поняттями див. далі в розділі "Кореляційні функції випадкових процесів"). Одновимірна густина ймовірності і пов'язані з нею числові характеристики дозволяють отримати важливу інформацію про властивості випадкового процесу. Проте для вирішення багатьох завдань таких відомостей недостатньо, оскільки вони дають ймовірнісне уявлення про випадковий процес Х(t) тільки в окремі моменти і ничего не говорять про те, як він змінюється в часі. Для описання його часових характеристик необхідно використовувати кореляційну функцію або притягнути для цього спектральні характеристики випадкового процесу. Згадані способи описаннягустин випадкових процесів будуть розглянуті далі.

 

2. Аналіз випадкових сигналів

Кореляційні функції випадкових процесів

Як відзначалося раніше, одновимірної густини ймовірності недостатньо для описання поведінки випадкового процесу в часі. Значно більше відомостей можна отримати, маючи в розпорядженні два перерізи випадкового процесу в довільні моменти часу t₁ і t₂ (див. рис. 6.1). Сукупність цих двох перерізів утворює двовимірну випадкову величину {X(t₁), X(t₂)}, яка описується двовимірною густиною ймовірності р(х₁, х₂, t₁, t₂). Добуток р(х₁, х₂, t₁, t₂)dx₁dx₂ є ймовірністю того, що реалізація випадкового процесу X(t) у момент часу t₁ потрапляє в нескінченно малий інтервал шириною dx₁ в околиці х₁, а в момент часу t₂ - в нескінченно малий інтервал шириною dx₂ в околиці х₂:

р(х₁, х₂, t₁, t₂)dx₁dx₂ = P{|X(t₁)-х₁| 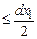, |X(t₂)-х₂| }.

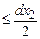Природним узагальненням є n-мірний переріз випадкового процесу, що призводить до n-мірної густини ймовірності р(х₁, х₂, ..., х _n , t₁, t₂,…, t_n). При 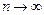 така функція є вичерпною ймовірнісною характеристикою випадкового процесу.

Опис властивостей випадкових процесів за допомогою багатовимірної густини ймовірності високої розмірності може бути дуже детальним, проте на цьому шляху часто зустрічаються серйозні математичні труднощі. На щастя, багато завдань, пов'язаних з описом випадкових сигналів, вдається вирішити на основі двовимірної щільності вірогідність.

Зокрема, завдання двовимірної густини ймовірності р(х₁, х₂, t₁, t₂) дозволяє визначити важливу характеристику випадкового процесу - його ковариац ій ну функцію

K_x(t₁, t₂) = M{x(t₁)x(t₂)}.

Згідно з цим визначенням, ковариаційна функція випадкового процесу X(t) є статистично усередненим добутком значень випадкової функції X(t) в моменти часу t₁ і t₂.

Для кожної реалізації випадкового процесу добуток x(t₁)x(t₂) є деяким числом. Сукупність реалізацій утворює безліч випадкових чисел, розподіл яких характеризується двовимірною густиною ймовірності р(х₁,х₂,t₁,t₂). Якщо ця густина ймовірності відома, операція усереднення по множині здійснюється по формулі

.

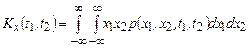Часто при аналізі випадкових процесів основний інтерес представляє їх флуктуаційна складова. У таких випадках застосовується кореляційна функція, що є статистично усередненим добутком значень центрованої випадкової функції    X(t)-m_x(t) в моменти часу t₁ і t₂

 

.

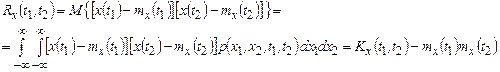Кореляційна функція характеризує міру статистичного зв'язку тих значень випадкового процесу, які спостерігаються при t = t₁ і t = t₂. При t₁= t₂ = t останній вираз відповідає визначенню дисперсії випадкового процесу X (див. формулу (6.2)). Отже, при поєднанні перерізів функція кореляції дорівнює дисперсії:

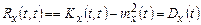. (R_x(t,t) = 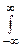x²p(x,t)dx-m_x²(t); (6.2))

 

ЗАУВАЖЕННЯ ----------------------------------------------------------------------------------------

Так склалося, що в іноземній літературі використовується зворотна термінологія - 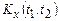 називається кореляційною (correlation), a  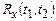ковариаційною функцією (covariance). Щоб уникнути непорозумінь про це слід пам'ятати при роботі із зарубіжними джерелами. Втім, при аналізі центрованих (що мають нульове математичне сподівання) випадкових процесів кореляційна і ковариаційна функції співпадають.

 

Як приклад розрахуємо кореляційну функцію гармонійного сигналу з випадковою рівномірно розподіленою початковою фазою (див. розділ "Моделі випадкових процесів" раніше в цій лекції).

Можна легко переконатися, що цей випадковий процес є центрованим, тобто його математичне очікування не залежить від часу і дорівнює нулю:

т_х(х)= 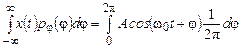= 0.

Тому ковариаційна і кореляційна функції цього процесу співпадають і можуть бути знайдені таким чином (оскільки реалізації цього випадкового процесу є функціями, залежними від однієї випадкової величини, для усереднювання добутку немає необхідності удаватися до двовимірної густини ймовірності - достатньо скористатися формулою M{f(x)}= 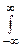f(x)p_x(x)dx для усереднення довільної функції від випадкової величини):

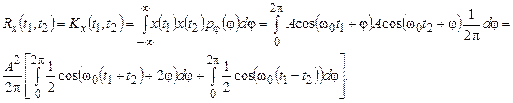
Тут в першому доданку інтегрування виконується по двох періодах функції cos, тому цей інтеграл дорівнює нулю. У другому доданку підінтегральна функція не залежить від змінної інтегрування φ, тому результат інтегрування дорівнює добутку підінтегрального виразу і довжини проміжку інтегрування 2π. Остаточно отримуємо

.

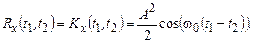Як бачите, кореляційна функція цього випадкового процесу гармонійно залежить від відстані між аналізованими моментами часу. При збігові моментів часу t₁= t₂ отримуємо величину дисперсії випадкового процесу

 

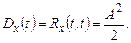
Некоррелированность і статистична незалежність

Якщо спільно розглядати дві випадкові величини Х₁ і Х₂, між ними може існувати або не існувати статистичний зв'язок. Відсутність такого зв'язку означає, що густина ймовірності однієї випадкової величини не залежить від того, якого значення набуває інша випадкова величина. Двовимірна густина ймовірності при цьому є добутком одновимірних густин

р(х₁,х₂) = р₁(х₁)р₂(х₂).

Ця умова називається умовою статистичної незалежності. За наявності статистичного зв'язку між випадковими величинами статистичні властивості кожної з них залежать від значення, що приймається іншою випадковою величиною. Цей зв'язок може бути сильним або слабким, лінійним або нелінійним. Мірою лінійного статистичного зв'язку між випадковими величинами є коефіцієнт кореляції

.

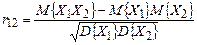Можна показати, що 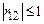. Граничні значення ±1 досягаються, якщо реалізації випадкових величин жорстко пов'язані лінійним співвідношенням х₂ = ах₁ + b, де а і b - деякі константи. Знак коефіцієнта кореляції при цьому сівпадає зі знаком множника а.

Рівність коефіцієнта кореляції нулю свідчить про відсутність лінійного статистичного зв'язку між випадковими величинами (при цьому говорять про їх некоррелированности). Як видно з цього виразу, при цьому математичне сподівання добутку випадкових величин дорівнює добутку їх математичних сподівань .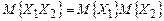

Легко показати, що із статистичної незалежності виходить некорельованість випадкових величин. Зворотне твердження в загальному випадку невірне - некорельовані випадкові величини можуть бути залежними.

ЗАУВАЖЕННЯ ---------------------------------------------------------------------------------------

Класичним прикладом цього є пара випадкових величин х₁ = cos φ і x₂=sin φ, де φ - випадкова величина, рівномірно розподілена на інтервалі 0...2π. Очевидно, що х₁ і x₂ залежать одина від одної; проте їх коефіцієнт кореляції виявляється рівним нулю.

 

Стаціонарні і ергодичні випадкові процеси

У загальному випадку, як вже говорилося, ймовірнісні і кореляційні характеристики випадкових процесів залежать від одного або декількох моментів часу, в які ці характеристики визначаються. Проте існує клас випадкових процесів, у яких залежність характеристик від часу відсутня. Крім того, для деяких випадкових процесів не обов'язково робити усереднювання по ансамблю реалізацій - можна обмежитися розглядом однієї реалізації і її усереднюванням в часі.

Такі випадкові процеси розглянемо далі.

 

Стаціонарні випадкові процеси

Це випадкові процеси, статистичні характеристики яких однакові в усіх часових перерізах. Говорять, що випадковий процес строго стаціонарний (чи стаціонарний у вузькому сенсі), якщо його багатовимірна густина ймовірності 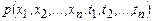 довільної розмірності n не змінюється при одночасному зрушенні усіх часових перерізів  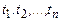уздовж осі часу на однакову величину τ:

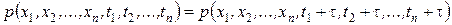 при будь-якому τ.

Якщо ж обмежити вимоги тим, щоб від часового зрушення не залежали лише одновимірна і двовимірна густини ймовірностей, то такий випадковий процес буде стаціонарний в широкому сенсі. Зрозуміло, що із стаціонарності у вузькому сенсі витікає стаціонарність в широкому сенсі, але не навпаки. Для стаціонарного випадкового процесу математичне сподівання і дисперсія не залежать від часу, а кореляційна функція залежить не від самих моментів часу, а тільки від інтервалу між ними τ = t₂ – t₁: R_x(t₁,t₂) = R_x(t₂-t₁)= R_x(τ).

З цієї причини при записі статистичних параметрів стаціонарного випадкового процесу можна опускати позначення фіксованих моментів часу: m_x, D_x, К_х(τ), R_x(τ).

Легко переконатися, що кореляційна функція стаціонарного випадкового процесу є парною:

R_x(-τ)=R_x(τ).

Крім того, абсолютні значення цієї функції при будь-яких τ не перевищують її значення при τ = 0 (нагадаємо, що це значення дорівнює дисперсії випадкового процесу):

|R_x(τ)| 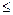R_x(0)=D_x.

Часто зручно використовувати коефіцієнт кореляції (його також називають нормованою кореляційною функцією)

r_x(τ)=R_x(τ)/D_x.

 

Для коефіцієнта кореляції виконуються співвідношення r_x(0)=1, |r_x(τ)| 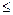1,   r_x(-τ)=r_x(τ).

Функції R_x(τ) і r_x(τ) характеризують зв'язок (кореляцію) між значеннями X(t), розділеними проміжком τ. Чим повільніше убувають ці функції із зростанням абсолютного значення τ, тим більше проміжок, протягом якого спостерігається статистичний зв'язок між миттєвими значеннями випадкового процесу, і тим повільніше, плавніше змінюються в часі його реалізації. Легко бачити, що гармонійний випадковий процес з випадковою початковою фазою (див. розділ "Моделі випадкових процесів" і обчислення характеристик цього процесу в розділі "Кореляційні функції випадкових процесів") є стаціонарним в широкому сенсі. Дійсно, залежні від одновимірної густини ймовірності математичне сподівання т_х(х)= 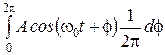=0 і дисперсія  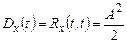не залежать від часу, а кореляційна функція 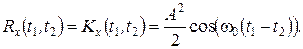, залежна від двовимірної густини ймовірності, залежить лише від інтервалу між даними моментами часу

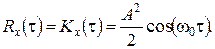
Коефіцієнт кореляції такого випадкового процесу дорівнює

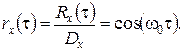
ЗАУВАЖЕННЯ --------------------------------------------------------

Тут слід зазначити, що стаціонарним буде будь-який випадковий процес, реалізації якого є періодичними функціями, ідентичними за формою і що відрізняються лише "початковою фазою", тобто положенням початку відліку часу в межах періоду. При цьому принциповою є рівномірність розподілу початкової фази в межах періоду. Дійсно, нехай у гармонійного процесу початкова фаза рівномірно розподілена в межах половини кола - на інтервалі 0...π. Математичне сподівання процесу в цьому випадку буде

т_х(х)= .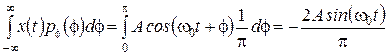

 

Результат обчислень показує, що математичне очікування процесу залежить від часу, отже, він не є стаціонарним.

 

Ергодичні випадкові процеси

Подальше спрощення аналізу випадкових процесів досягається при використанні умови ергодичності процесу. Стаціонарний випадковий процес називається эргодическим (ergodic), якщо при визначенні будь-яких його статистичних характеристик усереднювання по безлічі (ансамблю) реалізацій еквівалентно усереднюванню за часом (time averaging) однієї, теоретично нескінченно довгої, реализації.

Позначивши усереднення кутовими дужками, можна записати наступні вирази, що дозволяють обчислити важливі статистичні характеристики ергодичного процесу за його єдиною реалізацією x(t) (ерогдичний процес обов’язково є стаціонарним, але не навпаки)

т_х(х)= .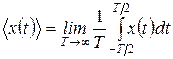

.

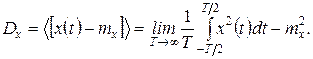
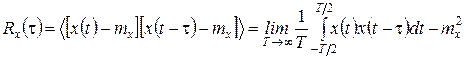Математичне сподівання ергодичного випадкового процесу дорівнює постійній складовій будь-якої його реалізації, а дисперсія має наочний фізичний зміст потужності флуктуаційної складової.

Достатньою умовою ергодичності випадкового процесу, стаціонарного в широкому сенсі, є прагнення до нуля його кореляційної функції із зростанням часового зсуву τ: .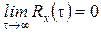

При експериментальному дослідженні випадкових процесів доступне, як правило, спостереження однієї реалізації сигналу, а не усього ансамблю. Якщо процес, що вивчається, є ергодичним, то його реалізація достатньої довжини є "типовим" представником статистичного ансамблю. Згідно з приведеними вище формулами по цій єдиній реалізації можна визначити математичне сподівання, дисперсію і кореляційну функцію ергодичного випадкового процесу. На практиці інтегрування виконується, природно, не в нескінченних границях, а на кінцевому інтервалі, довжина якого має бути тим більше, чим вище вимоги до точності результатів вимірювання.

Як приклад перевіримо ергодичність гармонійного процесу з випадковою початковою фазою (стаціонарність такого процесу була перевірена раніше). Його кореляційна функція 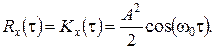 із зростанням τ не прагне до нуля, так що умова  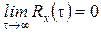не виконується. Проте це лише достатня, але не необхідна умова, тому його невиконання ще не означає неергодичності процесу. Перевіримо ергодичність згідно з визначенням, обчисливши усереднені за часом параметри:

,

,

.

 

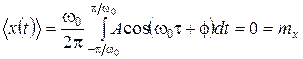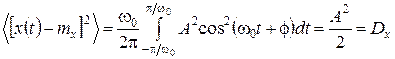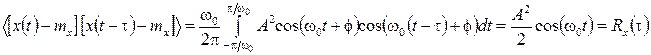ЗАУВАЖЕННЯ

Той факт, що реалізації даного процесу є періодичними функціями, дозволяє спростити обчислення, замінивши усереднювання по нескінченному (гранично) проміжку часу усереднюванням по одному періоду, рівному в даному випадку 2π/ω_о.

 

Отже, параметри, обчислені усереднюванням за часом, співпали з параметрами, отриманими раніше шляхом статистичного усереднювання. Отже, гармонійний випадковий процес з випадковою початковою фазою є ергодичним.

ЗАУВАЖЕННЯ

Тут також слід зазначити, що будь-який випадковий процес, реалізації якого є періодичними функціями, ідентичними за формою і що розрізняються лише рівномірно розподіленою в межах періоду "початковою фазою", буде не лише стаціонарним, але і ергодичним.

 

Нестаціонарні випадкові процеси

1. Аддитивні нестаціонарні процеси. До аддитивних нестаціонарних процесів відносяться процеси виду η(t) =ξ(t)+φ(t) , де ξ(t) - стаціонарний випадковий процес; φ(t) – деяка детермінована функція за умови φ(t) ≠ const.

2. Мультиплікативні нестаціонарні процеси. Такі процеси описуються одним з наступних співвідношень: η(t) =ξ(t)φ(t) або η (t) =ξ(t)γ(t), де ξ(t) і γ(t) - деякі випадкові функції, у тому числі і стаціонарні; φ(t) - довільна детермінована функція.

3.Квазистационарные (почти стационарные) процессы. Это такие случайные процессы, для которых справедливы соотношения

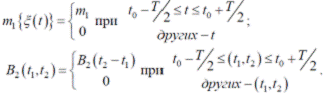
Тут T - інтервал фактичного існування випадкової функції ξ(t); t₀ - деякий довільний момент часу.

4. Періодичні і майже періодичні нестаціонарні процеси. Такі процеси визначаються по умові:

- для періодичних процесів

W_n(x₁,t₁; x₂,t₂;...; x_n,t_n ) =W_n (x₁,t₁+T; x₂,t₂+T;...; x_n,t_n +T),

тобто n-мірна густина ймовірності є періодичною функцією з періодом T від кожного з аргументів t₁, t₂,.., t_n;

- для майже періодичних процесів

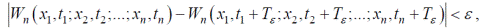
де ε - деяка позитивна скільки завгодно мала величина. Параметр T_ε носить назву "Майже період".

Спектральні характеристики випадкових процесів

 

Кожна окремо взята реалізація випадкового процесу є детермінованою функцією, і до неї можна застосувати перетворення Фур'є. При цьому різні реалізації будуть, природно, мати різні спектри. Нас же цікавлять статистично усереднені характеристики випадкових процесів. Спробуємо знайти середнє значення спектральної щільності випадкового процесу (горизонтальною рисою тут і далі позначається операція статистичного усереднювання по ансамблю реалізацій):

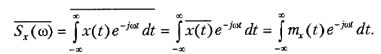
Як бачите, усереднена спектральна густина випадкового процесу є спектром його детермінованої складової (математичного сподівання). Для центрованих процесів 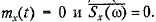Таким чином, усереднене значення спектральної густини не несе ніякої інформації про флуктуаційну, тобто власне випадковою, складовій випадкового процесу. Це говорить про те, що фази спектральних складових в різних реалізаціях процесу випадкові і незалежні.

Можна, проте, розглянути спектральну густину потужності випадкового процесу, оскільки потужність не залежить від співвідношення фаз спектральних складових.

Розглянемо центрований випадковий процес і виділимо з його ансамблю яку-небудь реалізацію 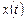, обмеживши її тривалість кінцевим інтервалом часу  [-T/2, T/2]. Застосувавши потім до цієї реалізації пряме перетворення Фур'є, знайдемо її спектральну густину 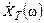. Енергію Е_Т даного відрізку реалізації згідно з рівністю Парсеваля (1.24) можна обчислити як

,

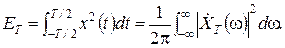Розділивши цю енергію на T, отримаємо середню потужність Р_Т реалізації на цьому часовому інтервалі:

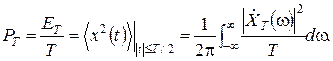
При збільшенні тривалості проміжку часу T енергія відрізку реалізації необмежено зростає, а середня потужність прагне до деякої границі. Зробивши граничний перехід 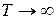, отримаємо

,

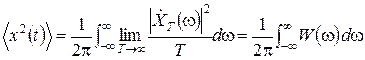де функція 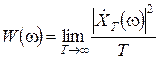 є спектральною густиною середньої потужності розглянутої реалізації.

 

ЗАУВАЖЕННЯ-------------------------------------------------------------- --------------------------

Часто говорять "спектральна густина потужності" або "спектр потужності". Англійський термін - power spectral density, PSD.

У загальному випадку спектральну густину потужності 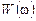 необхідно усереднити по безлічі реалізацій. Проте, якщо обмежитися розглядом ергодичних процесів, можна вважати, що знайдена по одній реалізації (тобто шляхом усереднювання за часом) функція  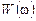характеризує увесь процес в цілому.

Оскільки ми розглядаємо центрований ергодичний випадковий процес, середня потужність будь-якої його реалізації дорівнює дисперсії процесу. Таким чином

.

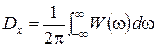 - дійсна функція, вона не містить інформації про фази спектральних складових і не дозволяє відновити окремі реалізації випадкового процесу. Крім того, з визначення спектральної густини 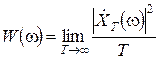 очевидно, що  є невід’ємною і парною функцією частоти.

 

ЗАУВАЖЕННЯ ----------------------------------------------------------------------------------------

Тут не приводиться прикладів розрахунку спектру випадкового процесу згідно з приведеним визначенням, оскільки такого роду розрахунок рідко потрібний на практиці. Як правило, обчислення спектру випадкового процесу виробляється на основі його кореляційної функції за допомогою теореми Винера-Хинчина, мова про яку піде далі.

 

Теорема Вінера-Хинчина

Як розподіл спектральної густини потужності, так і вид кореляційної функції пов'язані зі швидкістю зміни випадкового процесу в часі. Знайдемо зв'язок між цими двома характеристиками.

Як відомо, кореляційна функція детермінованого сигналу пов'язана перетворенням Фур'є з його енергетичним спектром. Застосуємо цю властивість до відрізку реалізації випадкового процесу тривалістю T

.

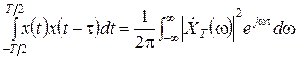Розділимо обидві частини цієї рівності на Т і спрямуємо Т до нескінченності

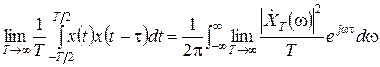                          . (6.3)

Якщо вважати даний процес ергодичним, то в лівій частині останньої рівності стоїть кореляційна функція процесу, отримана шляхом усереднювання за часом. У правій частині під інтегралом міститься вираз 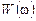 для спектральної густини потужності випадкового процесу. З урахуванням цього

.

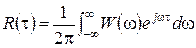ЗАУВАЖЕННЯ--------------------------------------------------------------------------------

У разі неергодичного процесу до обох частин рівності (6.3) необхідно додатково застосувати усереднювання по ансамблю реалізацій, що приведе до того ж самому результату.

 

Таким чином, кореляційна функція випадкового процесу і його спектральна густина потужності пов'язані одина з одною перетворенням Фур'є. Це співвідношення носить назву теореми Вінера-Хинчина.

Оскільки 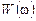і  і 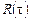 є парними дійсними функціями, можна відмовитися від комплексної форми запису перетворення Фур'є і перейти до напівнескінченних меж інтегрування :

, .

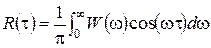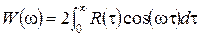При 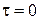 маємо 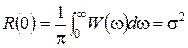. Дисперсія стаціонарного випадкового процесу, таким чином, є сумою внесків від усіх ділянок частотної вісі. На відміну від детермінованих імпульсних сигналів,  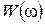характеризує питому міру потужності, а не частку енергії, яка припадає на одиничну смугу частот. 

Дуже часто використовувана модель випадкового процесу виявляється такою, що скористатися безпосередньо визначенням 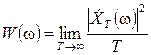 для розрахунку спектральної густини потужності неможливо. Якщо при цьому вдається обчислити кореляційну функцію, отримати спектральну інформацію дозволяє теорема Вінера-Хинчина.

Теорема Вінера-Хинчина у наданому вище вигляді стосується випадкових процесів з нульовим середнім. У загальному ж випадку існує зв’язок

, .

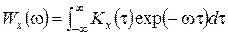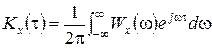Інтервал кореляції

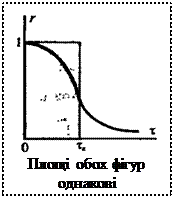Випадкові процеси, що зустрічаються в задачах обробки сигналів і вивчаються в радіотехніці, часто мають наступну властивість: їх функція кореляції прагне до нуля із збільшенням часового зсуву τ (нагадаємо, що це є достатньою умовою ергодичності процесу). Чим швидше убуває функція R(τ), тим слабкіше виявляється статистичний зв'язок між миттєвими значеннями випадкового сигналу в два неспівпадаючі моменти часу. Числовою характеристикою, що слугує для оцінки "швидкості зміни" реалізацій випадкового процесу, є інтервал кореляції τ_k, визначається як

.

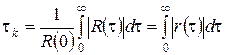Якщо відома інформація про поведінку якої-небудь реалізації випадкового процесу "у минулому", то можливий імовірнісний прогноз випадкового процесу на час порядку τ_k. Прогнозування на інтервал часу, який суттєво перевищує τ_k виявляється безрезультатним, оскільки миттєві значення стають практично некорельованими.

 

Ефективна ширина спектру

Нехай досліджуваний випадковий процес характеризується спектром густини потужності 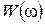, що має максимальне значення 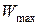. Замінимо подумки цей випадковий процес іншим, у якого спектральна густина потужності постійна і дорівнює  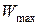в межах деякої смуги частот, яка обрана з умови рівності дисперсій (тобто середніх потужностей) обох процесів. Ширина цієї смуги частот називається ефективною шириною спектру випадкового процесу:

, .

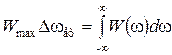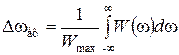Ефективну ширину спектру випадкового процесу можна визначити й іншими способами, наприклад, виходячи з умови зменшення значень спектру потужності на межі цього частотного інтервалу до рівня 0,1 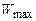. У будь-якому випадку величини  τ_k і  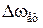пов'язані відомим з властивостей перетворення Фур'є співвідношенням невизначеності 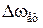τ_k ~ _.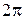

Для ілюстрації цього співвідношення на мал. 6.3 в центрі наведені приклади реалізацій двох випадкових процесів, ліворуч - кореляційні функції цих процесів, а справа - їх спектри щільності середньої потужності.

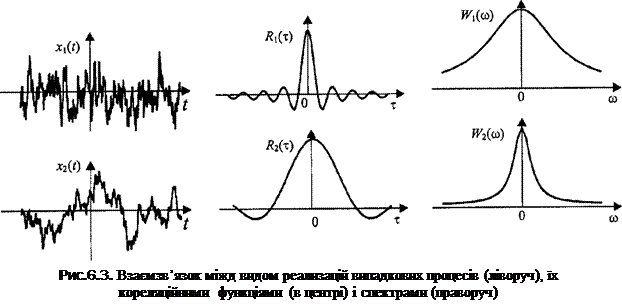
Білий шум

У радіотехніці білим шумом (white noise) називають стаціонарний випадковий процес, спектральна щільність потужності якого постійна на усіх частотах

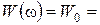const.

Згідно з теоремою Винера-Хинчина, кореляційна функція білого шуму є дельта-функцією:

,

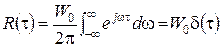тобто дорівнює нулю усюди, окрім точки τ = 0. Дисперсія білого шуму нескінченно велика.

У неспівпадаючі моменти часу значення білого шуму некорельовані - яким би не був малим інтервал τ, сигнал за цей час може змінитися на будь-яку величину.

Білий шум є абстрактною математичною моделлю і фізично існувати не може. Це пояснюється передусім нескінченністю його дисперсії (тобто середньої потужності). Проте в тих випадках, коли смуга пропускання досліджуваної системи істотно вужча за ефективну ширину спектру шуму, який на неї впливає, можна для спрощення аналізу приблизно замінити реальний випадковий процес білим шумом.

 

ЗАУВАЖЕННЯ ----------------------------------------------------------------------------------------

Відзначимо ще раз, що ймовірнісні і кореляційні (чи спектральні) характеристики випадкового процесу - це абсолютно різні і не пов'язані між собою функції. Так, наприклад, нормальний випадковий процес може мати різноманітну спектральну густину потужності, а білий шум - довільну функцію розподілу. Єдина "точка зіткнення" імовірнісних і кореляційних характеристик - це можливість розрахунку дисперсії випадкового процесу як на основі одновимірної густини ймовірнісні D_x(t)=M{[X(t)-m_x(t)]²}= 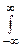x²p(x,t)dx-m_x²(t), так і виходячи з кореляційної функції .

---

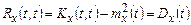Дата добавления: 2022-01-22; просмотров: 35; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!