Властивості розкладання в ряд Фур'є (особливості спектрів періодичних сигналів) .

Розглянемо їх на прикладі комплексно-експоненційого ряду Фур'є.

1. Дві характеристики — амплітудна і фазова, тобто, модулі та аргументи комплексних коефіцієнтів ряду Фур'є повністю визначають спектр періодичного сигналу.

2. Властивість дискретності або лінійчастості. Спектр періодичного сигналу дискретний або лінійчастий. Він складається з окремих ліній (точок) на відповідних частотах …, - 2ω₁, - ω₁, 0, ω₁, 2ω₁, … .

3. Властивість еквідистантності. Спектри періодичних сигналів еквідистантні, тобто спектральні лінії знаходяться одна від одної на відстані ω₁= 2π/Т. Частота ω₁ називається частотою першої гармоніки.

4. Властивість симетрії. Коефіцієнти ряду Фур'є, а отже й спектри симетричні відносно частоти ω= 0. Цією властивістю спектрів ми вже користувалися, тепер розглянемо її детальніше.

Якщо сигнал s(t) є дійсною функцією часу, перша складова правої частини є дійсною складовою коефіцієнта , а друга складова - уявною складовою. Тому можна записати

З цього виразу виходить, що

Оскільки отримуємо, що та , .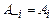

Таким чином, якщо сигнал s(t) є дійсною функцією часу, то модулі коефіцієнтів ряду Фур'є мають властивість парної симетрії відносно i, отже й частоти, а аргументи - властивість непарної симетрії відносно i (частоти).

5. Якщо s(t) є дійсною й парною функцією часу, то уявна частина коефіцієнтів ряду Фур'є дорівнює нулю або, що те саме, коефіцієнти синус-косинусного ряду Фур'є b_i = 0.

З умови == -arctg(b_i /a _i) виходить, що може набувати лише двох значень: 0 або ±π.

Якщо s(t) є дійсною і непарною функцією часу, то дійсна частина коефіцієнтів ряду Фур'є дорівнює нулю або, що те саме, коефіцієнти синус-косинусного"ряду Фур'є a _i = 0. У цьому випадку може набувати лише двох значень: π/2 або -π/2.

6. Якщо сигнал s(t) має властивість непарної напівперіодичної симетрії, то = 0 при i = 0, ±2, ±4, ±6, ... . Умова непарної напівперіодичної симетрії записується так:

s(t) = -s(t±T/2), -∞<t<∞.

7. Теорема Парсеваля для періодичних сигналів. Знайдемо середню потужність сигналу s(t).

Раніше в лекції 2 було показано, що середню потужність періодичного сигналу можна знайти за формулою

середня потужність періодичного сигналу є сумою потужності сталої складової і потужностей гармонічних складових сигналу.

Приклади розкладання сигналів в ряд Фур'є

Застосуємо ряд Фур'є для аналізу конкретних сигналів.

Послідовність прямокутних імпульсів

Розглянемо послідовність прямокутних імпульсів з амплітудою A, тривалістю τ і періодом повторення Т. Початок відліку часу приймемо розташованим в середині імпульсу (Рис. 2)

Рис. 3.2. Періодична послідовність прямокутних імпульсів

Цей сигнал є парною функцією, тому для його представлення зручніше використовувати синусно-косинусну форму ряду Фур'є - в ній будуть присутні тільки косинусні доданки

отримані з використанням замін

В отриманій формулі можна помітити, що тривалість імпульсів і їх період слідування входять в неї не відокремлено, а виключно у вигляді відношення. Цей параметр - відношення періоду до тривалісті імпульсів - називають шпаруватістю послідовності імпульсів і означають буквою q: q = T/τ. Введемо цей параметр в отриману формулу для коефіцієнтів ряду Фур'є, а потім приведемо формулу до виду sin (х)/х.

Зауваження : У зарубіжній літературі замість шпаруватості використовується зворотна величина, яка має назву коефіцієнт заповнення (duty cycle) і рівна τ/T. При такій формі запису добре помітно чому дорівнює значення постійної складової ряду: оскільки при , тому .

Тепер можна записати і саме представлення періодичної послідовності прямокутних імпульсів у вигляді ряду Фур'є

(3)

Амплітуди гармонійних доданків ряду залежать від номера гармоніки по закону (рис. 3). Графік функції має пелюстковий характер. Говорячи про ширину цих пелюсток, слід підкреслити, що для графіків дискретних спектрів періодичних сигналів можливі два варіанти градуювання горизонтальної осі - в номерах гармонік і в частотах. На рис. 3,б (комплексне представлення) градуювання осі відповідає номерам гармонік, а частотні параметри спектру нанесені на графік за допомогою розмірних ліній.

а)

б)

Рис. 3.3. Спектр періодичної послідовності прямокутних імпульсів: амплітудний (а) дійсна форма, (б) комплексна форма; (в) фазовий спектр

Отже, ширина пелюсток, виміряна у кількості гармонік, дорівнює шпаруватості послідовності (при i = q маємо ). Звідси витікає важлива властивість спектру послідовності прямокутних імпульсів - в ньому відсутні (мають нульові амплітуди) гармоніки з номерами, кратними шпаруватості.

Відстань по частоті між сусідніми гармоніками дорівнює частоті слідування (повторення) імпульсів - 2π/T. Ширина пелюсток спектру, виміряна в одиницях частоти, рівна 2π/τ, тобто зворотно пропорційна тривалості імпульсів. Це, як ми побачимо далі, прояв загального закону (для вузькосмугових, немодульованих сигналів) - чим коротше сигнал, тим ширше його спектр.

Меандр є важливим, відомим вже вам, окремим випадком попереднього сигналу - послідовність прямокутних імпульсів з шпаруватістю, що дорівнює двом, коли тривалість імпульсів і проміжків між ними стають рівними (рис. 4).

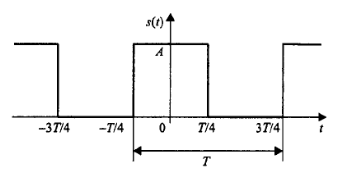
Рис. 3.4. Меандр

У цьому випадку q=2 і коефіцієнти ряду

Тут m – довільне ціле число.

Таким чином, в спектрі меандру присутні тільки непарні гармоніки. Це узгоджується із загальним правилом, приведеним вище (парна функція). Представлення меандру у вигляді ряду Фур'є з урахуванням цього може бути записане таким чином:

Гармоніки, з яких складається меандр, мають амплітуди, обернено пропорційні до номерів гармонік, і знаки, що чергуються.

Якщо мендр має різнополярні напівперіоди (рис. 5)

Рис. 3.5. Представлення меандру різнополярними імпульсами

Представлення періодичної послідовності прямокутних імпульсів типу меандр у вигляді ряду Фур'є, як видно з рис. 5, можна виконати як для непарної функції (рис. 5,а), так і для парної (рис. 5,б).

У випадку непарної функції (рис. 5,а)

У разі парної функції (рис. 5,б)

На відміну від попереднього випадку відсутня постійна складова, що пояснюється змінністю поляності сигналу на половині періоду, а цей доданок, як вже зазначалося, є середнім значенням сигналу на періоді: . Як і раніше, сума ряду включає лише непарні гармоніки (рис. 6). Значення цих гармонік зворотно пропорційні їх номеру.

Рис. 3.6. Коефіцієнти комплексного (а) і тригонометричного (б) ряду Фур’є меандру з різнополярними імпульсами (рис. 5)

Взагалі, послідовність прямокутних імпульсів погано підходить для представлення рядом Фур'є - вона містить скачки, а сума будь-якого числа гармонік з будь-якими амплітудами завжди є безперервною функією. Тому поведінка ряду Фур'є в околицях розривів представляє особливий інтерес. На графіках рис. 7 добре видно, що в околиці точки розриву підсумовування ряду Фур'є дає похилу ділянку, причому крутизна нахилу зростає із зростанням числа підсумовуваних гармонік. У самій точці розриву ряд Фур'є сходиться до напівсуми правої і лівої границь.

Рис. 7. Проміжні стадії підсумовування ряду Фур'є для меандру

На ділянках, що примикають до розриву, сума ряду Фур'є дає помітні пульсації, причому на графіках рис. 7 помітно, що амплітуда цих пульсацій не зменшується із зростанням числа підсумовуваних гармонік - пульсації лише стискуються по горизонталі, наближаючись до точки розриву. Це явище, властиве рядам Фур'є для будь-яких сигналів з розривами першого роду (скачками), називається ефектом Гіббса. Амплітуда першого (найбільшого) викиду складає приблизно 9 % від величини стрибка.

В процесі підготовки до лабораторної роботи вам слід розібрати інші приклади розкладання періодичних сигналів в ряд Фур’є [1]:

Пилкоподібний (в межах періоду він описується лінійною функцією (рис. 8):

, .

Рис. 8. Пилкоподібний сигнал

Ряд Фур'є для пилкоподібного сигналу виглядає наступним чином:

Тут .

У розглянутих вище спектрів прямокутного і пилкоподібного періодичних сигналів є одна загальна риса - амплітуди гармонік із зростанням їх номерів убувають пропорційно до і. У наступного сигналу швидкість загасання спектру буде іншою, а чому, ми обговоримо після розрахунку коефіцієнтів ряду Фур'є для нього.

Послідовність трикутних імпульсів(рис. 9)

Отримаємо розкладання в ряд Фур'є. Строго кажучи, імпульси в попередньому сигналі теж були трикутними, але в даному випадку вони матимуть не пилкоподібну, а симетричну форму (рис. 9):

, .

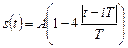Рис. 9. Послідовність трикутних импульсів

Обчислимо коефіцієнти ряду Фур'є (сигнал є парною функцією, тому в синусно-косинусній формі ряду Фур'є (1.6) будуть присутні тільки косинусні доданки):

Як і у разі меандру, тут присутні тільки парні гармоніки. Сам ряд Фур'є має наступний вигляд:

Як бачите, на відміну від послідовностей прямокутних і пилкоподібних імпульсів, для трикутного періодичного сигналу амплітуди гармонік убу-вають пропорційно квадрату номерів гармонік і. Це прояв загального правила: швидкість убування спектру залежить від міри гладкості сигналу. Прямокутний і пилкоподібний сигнали мають розриви першого роду (скачки), і в їх спектрах присутній множник 1/і. Трикутний сигнал є безперервною функцією (але її перша похідна має розриви), і амплітуди гармонік цього ряду Фур’є містять множник 1/і². Екстраполювавши цю залежність, отримаємо наступне правило: якщо N - номер останньої безперервної похідної сигналу, то спектр цього сигналу убуватиме із швидкістю 1/i^N^-2. Граничним випадком є гармонійний сигнал, диференціювати який без втрати безперервності можна нескінченно. Згідно із загальним правилом, це дасть нескінченну швидкість убування спектру, що цілком відповідає дійсності (ряд Фур’є для гармонійного сигналу містить тільки одну гармоніку).

Дещо забігаючи наперед, розгянемо амплітудно-маніпульовані сигнали, які є важливим класом багатотональних АМ-сигналів. У простому випадку це послідовності радіоімпульсів, відокремлених один від одного паузами. Такі сигнали використовуються в радіотелеграфії і в системах передачі дискретної інформації по радіоканалах. Тобто це сигнали, які мають гармонічну несучу, а її огинаючі можуть бути, наприклад, такими послідовностями періодичних імульсів, які ми вище розглядали і ви більш докладно розглянете ще вдома.

Розгляд таких сигналів нам потребн для того, щоб при проведенні лабораторної работи було зрозуміло, яким чином отримуються спектри послідоностей імпульсів за допомогою лабораторного аналізатора спектру.

Якщо s(t) - функція, в кожен момент часу що набуває значення або 0, або 1, то амплітудно-маніпульований сигнал, представляється у вигляді

Осцилограма амплітудно-маніпульованого сигналу

Нехай, наприклад, функція s(t) є періодична послідовність відеоімпульсів, розглянута вище (див. рис. 2). Вважаючи, що амплітуда цих імпульсов А = 1, при маємо

де q - шпаруватість послідовності. Фактично ми комплексний амплітудний спектр періодичної послідовності прямоктних імпульсів (3) зсунутий на частоту несучої частоти (див. рис. 3,б). Це дозволить нам використовувати спеутроаналізатор, який функціонує в діапазоні частот значно вищих за 0, для дослідження спектрів послідовностей імпульсів різної форми на лабораторному занятті. Як бачимо, у цьому випадку частоти, які відповідають від’ємним індексам можуть бути наявні в реальному спектрі сигналу, тому на практиці ми маємо можливість спостерігати комплексну форму ряду Фур’є послідовності імпульсів, яка є огинаючою, наприклад, радіосигналу.

ЛІТЕРАТУРА

1. Цифровая обработка сигналов / А. Б. Сергиенко — СПб.: Питер, 2002. — 608 с: ил.. (Электронный ресурс)

2. Волощук Ю.Л. Сигнали та процеси в радіотехніці том. 1. - Харків: «СМІТ», 2003.

3. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. – 512 с. 4. Баскаков С.И. Радиотехнические цепи и сигналы. - М.: «Высшая школа» 2003.

5. Сато Ю. Обработка сигналов. Первое знакомство. – ОΔЕКА, 1999. – 175 с.

Дата добавления: 2022-01-22; просмотров: 31; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!