Диференціювання складної функції
Теорема 4. Нехай на множині D визначена складна фун кція 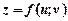 , де
, де  ,
,  і нехай функції
і нехай функції  ,
,  мають у деякому околі точки
мають у деякому околі точки  неперервні частинні похідні, а функція
неперервні частинні похідні, а функція 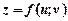 - неперервні частинні похідні в деякому околі точки
- неперервні частинні похідні в деякому околі точки  , де
, де  ,
,  . Тоді складна функція
. Тоді складна функція  диференційовна в точці
диференційовна в точці 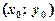 , причому
, причому
 ,
,  .
.
Приклад. Знайти 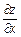 і
і  для функції
для функції  .
.
Маємо  де
де 
 .
.
Тоді  ,
, 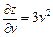 ,
,  ,
,  ,
,  ,
,  .
.
Таким чином,  ,
,  , або після підставляння виразів u і v дістанемо
, або після підставляння виразів u і v дістанемо  ,
,  .
.
Дотична площина та нормаль
Якщо функція  диференційовна в точці
диференційовна в точці  , то виконується рівність
, то виконується рівність

або

Узявши в цій наближеній рівності  ,
,  , дістанемо:
, дістанемо:
 (1)
(1)
На формулі (1) ґрунтується алгоритм використання диференціала для наближених обчислень.
Крім того, якщо в рівності (1) взяти  ,
,  , дістанемо
, дістанемо

Це рівняння дотичної площини, що проходить через точку  .
.
Якщо поверхню задано у просторі рівнянням  , то рівняння дотичної площини до поверхні
, то рівняння дотичної площини до поверхні  в точці
в точці  має вигляд:
має вигляд:
 , (2)
, (2)
де  ,
,  ,
,  .
.
Нормаль до поверхні в точці  - це пряма, що проходить через точку
- це пряма, що проходить через точку  і перпендикулярна до дотичної площини. Отже, її рівняння
і перпендикулярна до дотичної площини. Отже, її рівняння
 .
.
Похідна за напрямом. Градієнт
Означення 5 . Нехай функція  визначена в деякому околі точки
визначена в деякому околі точки  ;
;  — деякий промінь з початком у точці
— деякий промінь з початком у точці  ;
;  — точка на цьому промені, яка належить околу, що розглядається (рис. 5.19);
— точка на цьому промені, яка належить околу, що розглядається (рис. 5.19);  — довжина відрізка
— довжина відрізка  . Границя
. Границя  , якщо вона існує, називається похідною функції
, якщо вона існує, називається похідною функції  за напрямом
за напрямом  у точці
у точці  і позначається
і позначається  .
.
|
|
|

Рис. 2
Зокрема, 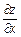 є похідна функції
є похідна функції 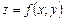 за додатним напрямом осі Ох, а
за додатним напрямом осі Ох, а  — похідна функції
— похідна функції 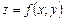 за додатним напрямом осі Оу.
за додатним напрямом осі Оу.
Похідна за напрямом  характеризує швидкість змінювання функції
характеризує швидкість змінювання функції  у точці
у точці  за напрямом
за напрямом  .
.
Теорема 5. Якщо функція  має в точці
має в точці  неперервні частинні похідні, тоді в цій точці існує похідна
неперервні частинні похідні, тоді в цій точці існує похідна  за будь-яким напрямом
за будь-яким напрямом  , причому
, причому
 ,
,
де  і
і  — значення частинних похідних функції
— значення частинних похідних функції  у точці
у точці  .
.
Приклад. Знайти похідну функції  у точці (1; 1) за напрямом
у точці (1; 1) за напрямом  .
.
Знайдемо та обчислимо частинні похідні в точці (1; 1) функції 
 ,
,  .
.
Тоді за формулою похідної за напрямом дістанемо:
 .
.
Означення 6 . Вектор з координатами  , який характеризує напрям максимального зростання функції
, який характеризує напрям максимального зростання функції 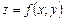 у точці
у точці  , називаєтьсяградієнтом функції
, називаєтьсяградієнтом функції 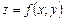 у цій точці і позначається
у цій точці і позначається 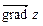 (
(  — одиничні орти):
— одиничні орти):

Аналогічно для функції трьох змінних  похідна за напрямом
похідна за напрямом  подається у вигляді:
подається у вигляді:

Для функції трьох змінних  градієнт у точці
градієнт у точці  визначається так:
визначається так:

де  — одиничні орти і
— одиничні орти і  обчислені в точці
обчислені в точці  .
.
Похідна за напрямом  функції
функції 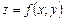 та градієнт пов’язані співвідношенням
та градієнт пов’язані співвідношенням 
Приклад. Знайти градієнт функції  у точці (1; 2; –1).
у точці (1; 2; –1).
Знайдемо та обчислимо частинні похідні в точці (1; 2; –1):
 ,
,  ,
,
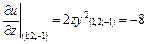 .
.
Тоді 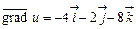 .
.
Приклад. Знайти точки, в яких модуль градієнта функції 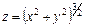 дорівнює 2.
дорівнює 2.
|
|
|
Знайдемо  і
і  :
:
 ,
,  .
.
Модуль градієнта дорівнює 2 в деякій точці  :
:
 .
.
Отже,  , тобто в точках кола з центром у точці (0; 0) і радіусом
, тобто в точках кола з центром у точці (0; 0) і радіусом  модуль градієнта заданої функції дорівнює 2.
модуль градієнта заданої функції дорівнює 2.
Дата добавления: 2022-01-22; просмотров: 21; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
