ОСНОВЫ ТЕОРИИ КОНЕЧНЫХ АВТОМАТОВ
1. Основные определения. В контактных и логических схемах значения выходных переменных определяются только комбинацией значений переменных на входах в данный момент времени. Поэтому их называют комбинационными схемами. В более общем случае выходные переменные могут зависеть от значении входных переменных не только в данный момент, но и от их предыдущих значений. Иначе говоря, значения выходных переменных определяются последовательностью значений входных переменных, в связи, с чем схемы с такими свойствами называют последовательностными. Если входные и выходные переменные принимают значения из конечных алфавитов, то оба типа схем объединяются под названием конечные автоматы.
Пусть X i - алфавит входной переменной х i , а Yi – алфавит выходной переменной yi. Конечный автомат с n входами и т выходами характеризуется входным алфавитом Х = Х1 ´ Х2 ´ ... Х n и выходным алфавитом Y = Y1 ´ Y2 ´ ... Y m, причем символами входного алфавита служат слова x = (x 1, x 2, …, xn) длины n, а символами выходного алфавита - слова y = (y 1, y 2, …, ym) длины т, где xi Î Xi и yi Î Yi. Особого внимания заслуживают конечные автоматы с двузначным структурным алфавитом, зависимости между входными и выходными переменными
которых выражаются булевыми санкциями. Их значение обусловлено тем, что любая информация может быть представлена в двоичных кодах (двоично-десятичные коды чисел, телетайпный код в технике связи и т.п.). В то же время при технической реализации автоматов используются преимущественно двоичные элементы и двузначная логика.
|
|
|
В реальных условиях сигналы представляются непрерывными функциями времени, поэтому для надежного различения сигналов требуется, чтобы новые значения на входах появлялись после окончания переходных процессов, связанных с предыдущими значениями. При рассмотрении логической структуры автоматов обычно отвлекаются от существа этих процессов и считают, что переменные изменяются не непрерывно, а мгновенно в некоторые моменты времени, называемые тактами. Интервалы между тактами могут быть различными, но без потери общности их можно считать равными  . Предполагается, что тактовые моменты
. Предполагается, что тактовые моменты  определяются синхронизирующими сигналами. Таким образом, вводится понятие дискретного автоматного времени t n(n = 1, 2, ...), причем переменные зависят не от физического времени, а от номера такта n, т. е. вместо непрерывных функций x(t) рассматриваются дискретные значения х(n).
определяются синхронизирующими сигналами. Таким образом, вводится понятие дискретного автоматного времени t n(n = 1, 2, ...), причем переменные зависят не от физического времени, а от номера такта n, т. е. вместо непрерывных функций x(t) рассматриваются дискретные значения х(n).
2. Состояния. Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой автомата. В комбинационных схемах промежуточные переменные непосредственно не участвуют в соотношениях вход - выход. Напротив, выходные функции последовательностных схем в качестве своих аргументов, кроме входных переменных, обязательно содержат некоторую совокупность промежуточных переменных s1, s2, …, sk, характеризующих состояние схемы. Набор всех возможных состоянии, которые присущи данной схеме, называется множеством состояний. Если S1, S2, …, Sk - конечные алфавиты переменных состояния s1, s2, …, sk, то множество состояний S = S1 ´ S2 ´ … ´ Sk также является конечным множеством.
|
|
|
Строгое определение понятия состояния связывается с той ролью, которое оно играет при описании конечных автоматов. Во-первых, значения совокупности выходных переменных на n-м такте у(n) = (y 1(v), y 2(n), …, y m(n)), однозначно определяется значениями входных переменных x(n) = (x 1(n), x 2(n), …, x n(n)) и состоянием s(n) = (s 1(n), s 2(n), …, s k(n)), на том же такте, т.е. у(n) = 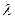 (x(n), s(n)). Во-вторых, состояние s(n + 1) в следующем (n + 1)-м такте однозначно определяется входными переменными х(n) и состоянием s(n) в предыдущем такте, т.е. s(n + 1) =
(x(n), s(n)). Во-вторых, состояние s(n + 1) в следующем (n + 1)-м такте однозначно определяется входными переменными х(n) и состоянием s(n) в предыдущем такте, т.е. s(n + 1) =  (x(n), s(v)).
(x(n), s(v)).
Таким образом, состояние конечного автомата в любой тактовый момент характеризуется значениями такой совокупности переменных, которая вместе с заданными значениями входных переменных позволяет определить выходные переменные в данный тактовый момент и состояние в следующий тактовый момент.
|
|
|
Ясно, что последовательностные схемы должны обладать способностью сохранять предыдущее состояние до следующего такта, в связи с чем их называют также автоматами с памятью или последовательностными машинами. В качестве памяти могут использоваться элементы задержки, на выходах которых повторяются входные воздействия со сдвигом во времени на интервал между тактами Dt. Широко применяются также различные запоминающие элементы, например, триггеры, способные сохранять состояния на выходах до тех пор, пока оно не изменяется в результате воздействия на их входы.

 3. Типы конечных автоматов. В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства чело века или с его ограниченным участием. Однако такое понимание является слишком узким. В широком смысле конечный автомат - это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы. Такая модель успешно используется как в технике (проектирование электронных вычислительных машин, систем управления и связи), так и в других областях - психологии и физиологии (исследование деятельности нервной системы человека и простейших видов поведения животных), лингвистике (анализ синтаксиса русского, английского или других языков, расшифровка древних рукописей), теории и практике административного управления и т.п. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогии между ними, переносить результаты из одной области в другую.
3. Типы конечных автоматов. В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства чело века или с его ограниченным участием. Однако такое понимание является слишком узким. В широком смысле конечный автомат - это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы. Такая модель успешно используется как в технике (проектирование электронных вычислительных машин, систем управления и связи), так и в других областях - психологии и физиологии (исследование деятельности нервной системы человека и простейших видов поведения животных), лингвистике (анализ синтаксиса русского, английского или других языков, расшифровка древних рукописей), теории и практике административного управления и т.п. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогии между ними, переносить результаты из одной области в другую.
|
|
|
Конечный автомат М определяется как система с конечным входным алфавитом Х = {  }, конечным выходным алфавитом Y = {v1, v2, …, vq}, конечным множеством состояний S = {
}, конечным выходным алфавитом Y = {v1, v2, …, vq}, конечным множеством состояний S = { 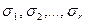 }, и двумя характеристическими функциями:
}, и двумя характеристическими функциями:
s(n + 1) =  (x(n), s(n));
(x(n), s(n));
у(n) = 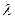 (х(n), s(n)),
(х(n), s(n)),
называемыми соответственно функцией переходов и функцией выходов. Общая блок-схема конечного автомата (рис. 27) может быть представлена в виде комбинационной схемы, реализующей характеристические функции d и l, и памяти, сохраняющей на один такт предыдущее состояние автомата.
В определении автомата участвует три конечных множества X, У, S и две функции  и
и 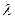 , задающие некоторые отношения между элементами этих множеств. Следовательно, конечный автомат можно обозначить упорядоченной пятеркой М = (X, У, S, d, l). Мощности множеств X, Y, S равны соответственно:
, задающие некоторые отношения между элементами этих множеств. Следовательно, конечный автомат можно обозначить упорядоченной пятеркой М = (X, У, S, d, l). Мощности множеств X, Y, S равны соответственно:

где pi , qi , ri - количество символов в алфавитах входной переменной xi, выходной переменной y i и переменной состояния si. При двоичном структурном алфавите р = 2n, q = 2m и r = 2k. Если желают подчеркнуть мощности множеств X, У и S, на которых определен конечный автомат, то его называют (р, q , r)-автоматом.
Характеристические функции  и
и 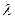 можно рассматривать как некоторые отображения множества X ´ S или его подмножества
можно рассматривать как некоторые отображения множества X ´ S или его подмножества  соответственно на множества S и У. Если
соответственно на множества S и У. Если  :
:  и
и 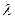 :
: 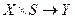 , автомат называется полным; если только
, автомат называется полным; если только  :
: 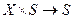 , автомат называют полным по переходам. В случае, когда функции
, автомат называют полным по переходам. В случае, когда функции  и
и 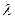 определены не для всех наборов из множества
определены не для всех наборов из множества  , автомат называют неполным или частично определенным.
, автомат называют неполным или частично определенным.
Приведенное в начале этого параграфа определение связывают обычно с автоматом первого рода, называемым также автоматом Мили. Если выходные переменные являются функцией только состояния, то имеем автомат второго рода или автомат Мура.
Между автоматами этих двух типов имеется взаимная связь и один из них может быть преобразован в другой. Положив в характеристических функциях автомата Мили s ¢(v) = (x(v), s(v)), получим у(v) = 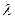 ¢(s ¢(v)) и s ¢(v + 1) = (x(v + 1), s(v + 1)) = (x(v + 1);
¢(s ¢(v)) и s ¢(v + 1) = (x(v + 1), s(v + 1)) = (x(v + 1);  (x(v), s(v))) =
(x(v), s(v))) =  (x(v + 1), s ¢(v)), т. е. приходим к автомату Мура. Обратный переход осуществляется подстановкой s(v) = s ¢(v - 1), в результате чего получаем у(v) =
(x(v + 1), s ¢(v)), т. е. приходим к автомату Мура. Обратный переход осуществляется подстановкой s(v) = s ¢(v - 1), в результате чего получаем у(v) = 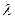 ¢(s ¢(v)) =
¢(s ¢(v)) = 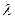 ¢(
¢(  (x(v), s ¢(v - 1))) =
(x(v), s ¢(v - 1))) = 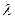 (x(v), s(v)), а также s(v + 1) = s ¢(v) =
(x(v), s(v)), а также s(v + 1) = s ¢(v) =  (x(v), s ¢(v - 1)) =
(x(v), s ¢(v - 1)) =  (x(v), s(v)).
(x(v), s(v)).
Для комбинационных схем функция перехода не имеет смысла, а функция выходов вырождается к виду y(v) = 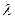 (x(v)). Их называют автоматами без памяти или тривиальными автоматами.
(x(v)). Их называют автоматами без памяти или тривиальными автоматами.
4. Представления конечных автоматов. Автомат может быть задан различными способами, например, путем словесного описания его функционирования или перечислением элементов множеств X, У, S, с указанием отношений между ними. При анализе и синтезе конечных автоматов используются стандартные формы представления: таблицы, графы и матрицы. Элементы множеств X, У, S удобно пронумеровать порядковыми числами, начиная с нуля, например: Х = {0, 1, 2, 3}, У = {0, 1} и S = {0, 1, 2, 3}. Тогда характеристические функции  и
и 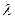 можно представить двумя таблицами, строки которых соответствуют состояниям, а столбцы - входам. Первая таблица, называемая таблицей переходов, соответствует функции s(v + 1) =
можно представить двумя таблицами, строки которых соответствуют состояниям, а столбцы - входам. Первая таблица, называемая таблицей переходов, соответствует функции s(v + 1) =  (x(v), s(v)), и ее клетки заполняются номерами состояний s(v + 1), в которые переходит автомат при
(x(v), s(v)), и ее клетки заполняются номерами состояний s(v + 1), в которые переходит автомат при
 |
воздействии х(v), и состоянию s(v) в данный тактовый момент. Вторая таблица, называемая таблицей выходов, соответствует функции у(v) =
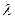 (x(v), s(v)), и ее клетки заполняются номерами выходов y(v) в данный тактовый момент, которые соответствуют воздействию x(v) и состоянию s(v) в тот же момент. Например, для заданных множеств X, У, S такие таблицы могут иметь вид:
(x(v), s(v)), и ее клетки заполняются номерами выходов y(v) в данный тактовый момент, которые соответствуют воздействию x(v) и состоянию s(v) в тот же момент. Например, для заданных множеств X, У, S такие таблицы могут иметь вид:
 |
Обе таблицы можно объединить в общую таблицу переходов, если условиться записывать в клетках пары чисел (номер следующего состояния в числителе и номер выхода в знаменателе), т.е.
 |
Граф автомата строится таким образом, что его вершины соответствуют состояниям, а направленные дуги обозначаются как дизъюнкции входов, под воздействием которых совершается переход из одного состояния в другое по направлению дуги. В знаменателях записываются номера выходов, соответствующие этим переходам.
На рис. 28 показан граф, построенный в соответствии с приведенной выше общей таблицей переходов. Так как из состояния 0 автомат переходит в состояния 1, 2 и 3, то из вершины О графа исходят дуги в вершины 1, 2 и 3. При этом переход в состояние 1 совершается под воздействием 2 нему соответствует выход 0, поэтому дуга из вершины 0 в 1 помечается как 2/0. Переход в состояние 2 совершается под воздействием 1 и ему соответствует выход 0, поэтому дуга из вершины 0 в 2 помечается как 1/0. Переходы в состояние 3 совершаются под воздействиями 0 и 3 и им обоим соответствует выход 0, поэтому дуга из вершины 0 в 3 помечается как дизъюнкция 0/0 Ú 3/0. Аналогично определяются и другие дуги графа. Петли соответствуют переходам, при которых состояния не изменяются. Так, рассматриваемый автомат переходит из состояния 2 в 2 под воздействиями 1 и 2, которым соответствуют выводы 0 и 1. Следовательно, петля при вершине 2 помечается как дизъюнкция 1/0 Ú 2/1.
Матрица соединения автомата М (или матрица переходов) представляет собой квадратную таблицу в которой номера строк и столбцов соответствуют номерам состояний. Клетка матрицы на пересечении i-й строки и j-го столбца заполняется дизъюнкцией пар «вход — выход», которая приписана дуге графа исходящей из i -й в j-ю вершину. При отсутствии такой ветви клетка заполняется нулем или остается свободной. Так для рассматриваемого примера имеем:
| 0 1 2 3 | ||||
|
М=
| 2/0 | 1/0 | 0/0 Ú 3/0 | |
| 2/0 | 1/0 | 0/1 Ú 3/1 | ||
| 1/0 Ú 2/1 | 0/1 Ú 3/1 | |||
| 1/0 Ú 2/1 | 3/1 | 0/0 | ||
5. Анализ конечных автоматов. Полное описание поведения автомата заключается в определении последовательности выходных сигналов при возбуждении его в тактовые моменты времени некоторой последовательностью входных сигналов. Входная и выходная последовательности представляются наборами символов (или их номеров) из алфавитов Х и У одинаковой длины l. Для такого описания, кроме характеристических функций, необходимо определить или задать начальное состояние автомата.
Наиболее удобно определять реакцию автомата на входною последовательность по его графу. Для этого достаточно проследить путь в графе, начиная от вершины начального состояния, по направлению дуг, которые отмечены очередными номерами на входной последовательности. Выходная последовательность определяется номерами, которыми отмечены дуги в порядке их следования по пройденному пути, а последовательность состоянии автомата номерами вершин, через которые проходит этот путь.
Так, из графа на рис. 28 для входной последовательности (2, 0, 1, 1, 2, 3) и начального состояния 0 имеем выходную последовательность (0, 1, 0, 0, 1, 1) и смену состояний автомата (1, 3, О, 2, 2, 3). При начальном состоянии 2 и той же входной последовательности получаем соответственно (1, 1, 0, 0, 1, 1) и (2, 3, 0, 2. 2, 3).
С помощью графа автомата легко выделить следующие характерные типы его состояний:
1) преходящее состояние, из которого можно перейти, но крайней мере, в одно другое состояние, но после этого уже нельзя возвратиться в него ни при каком воздействии (соответствующая вершина не имеет заходящих дуг, но имеет хотя бы одну исходящею дугу);
2) тупиковое состояние, в которое можно перейти, по крайней мере, из одного другого состояния, но после этого уже нельзя
выйти из него ни при каком воздействии (соответствующая вершина не имеет исходящих дуг в другие вершины, но имеет хотя бы одну входящую дугу из другой вершины);
3) изолированное состояние, из которого нельзя перейти ни в какое другое состояние и в него нельзя попасть ни из какого другого состояния (соответствующая вершина содержит только петлю).
Аналогичные определения можно дать для некоторых совокупностей состояний, рассматриваемых как подавтоматы. Если начальное состояние автомата М принадлежит непустому множеству Si состояний, которое составляет тупиковый или изолированный подавтомат, то M можно упростить исключением всех состояний, которые не принадлежат множеству Si, и всех дуг, начинающихся в этих состояниях.
Пусть М1, М2 и M 3 - соответственно преходящий, тупиковый и изолированные подавтоматы автомата М, которые характеризуются множествами состояний S 1, S 2 и S 3. Очевидно, выделение таких подавтоматов соответствует разбиению множества S состояний автомата М на непересекающиеся подмножества S 1, S 2 и S 3,представляющие собой классы эквивалентности 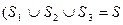 и
и  . Как следует из обобщенного графа (рис. 29), матрица соединения автомата может быть представлена в виде:
. Как следует из обобщенного графа (рис. 29), матрица соединения автомата может быть представлена в виде:
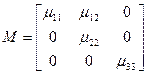 ,
,
где  - матрицы подавтоматов М1, М2 и М3;
- матрицы подавтоматов М1, М2 и М3; 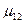 - матрица, характеризующая переходы от состояний преходящего автомата М1 к состояниям тупикового автомата М2. Отсюда следует, что разбиение автомата М на подавтоматы М1, М2 и М3 можно осуществить преобразованием его матрицы соединений к стандартному виду путем перестановки соответствующих строк и столбцов. Например, для автомата, граф которого изображен на рис. 30,
- матрица, характеризующая переходы от состояний преходящего автомата М1 к состояниям тупикового автомата М2. Отсюда следует, что разбиение автомата М на подавтоматы М1, М2 и М3 можно осуществить преобразованием его матрицы соединений к стандартному виду путем перестановки соответствующих строк и столбцов. Например, для автомата, граф которого изображен на рис. 30,
имеем:
| 3 6 2 4 7 1 5 | ||||
| М = | 0 2/0 1/0 0 | 0/1 0 1/1 0 1/0 2/1 | 0 0 0 0 | 3 6 2 4 7 1 5 |
| 0 0 0 0 0 0 | 1/1  2/0 0 0/0
1/0 2/0 0 0/0
1/0 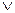 2/1 0/0 0
0 0/1 2/1 0/0 0
0 0/1 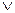 2/0 1/0 2/0 1/0
| 0 0 0 0 0 0 | ||
| 0 0 0 0 | 0 0 0 0 0 0 | 0/1 1/0 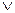 2/1
0/1 2/1
0/1 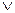 1/0 1/0 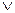 2/0 0 2/0 0
| ||
 |
Отсюда следует, что S 1 = {3, 6} составляет преходящий подавтомат, S 2 = {2, 4, 7} - тупиковый подавтомат и S 3 = {1, 5} - изолированный подавтомат. Если начальное состояние принадлежит множеству S 2, то можно упростить автомат, исключив состояния
 = {3, 6, 1, 5}, а в случае принадлежности начального состояния множеству S 3 автомат упрощается исключением состояний
= {3, 6, 1, 5}, а в случае принадлежности начального состояния множеству S 3 автомат упрощается исключением состояний  = {3, 6, 2, 4, 7}.
= {3, 6, 2, 4, 7}.
6. Синтез конечных автоматов. Реализация конечных автоматов сводится к синтезу соответствующей комбинационной схемы, преобразующей входные переменные x(v) и s(v) в выходные переменные y(v) и s(v + 1) в соответствии с заданными характеристическими функциями s(v + 1) =  (x(v), s(v)) и y(v) =
(x(v), s(v)) и y(v) = 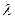 (x(v), s(v)). Для сохранения состояний s(v + 1) до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти.
(x(v), s(v)). Для сохранения состояний s(v + 1) до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти.
При реализации автоматов в двоичном структурном алфавите можно использовать рассмотренные ранее методы синтеза комбинационных схем. Но для этого необходимо закодировать состояния схемы н представить характеристические функции в виде булевых функций двоичных переменных. Такое кодирование можно осуществить преобразованием общей таблицы перехода автомата к таблице соответствия в двоичном структурном алфавите. Если элементы множеств X, У и S пронумерованы порядковыми числами, начиная с нуля, то им соответствуют коды, представляющие собой двоичные эквиваленты этих чисел. Например, для автомата, заданного в (4), таблицу переходов можно преобразовать к виду:
| x(v) s(v) | 0000 1111 2222 3333 0123 0123 0123 0123 |
| s(v + 1) y(v) | 3333 2220 1120 3331 0110 0000 0011 0111 |
Заменяя десятичные числа их двоичными эквивалентами, читаемыми сверху вниз, получаем таблицу соответствия, в которой значения функций s(v + 1) и у(v) представлены двоичными кодами:
|
| 0000 0000 1111 1111 0000 1111 0000 1111 |
| 0011 0011 0011 0011 0101 0101 0101 0101 | |
|
| 1111 1110 0010 1110 1111 0000 1100 1111 |
| 0110 0000 0011 0111 |
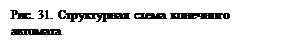

Отсюда видно, что комбинационная схема должна иметь четыре входа, соответствующие входным переменным x 1(v), х2(v) и переменным состояния s(v), s 2(v), а также три выхода, соответствующие переменным состояния s 1(v + 1), s 2(v + 1) и выходной переменной у1(v). Синтезировав комбинационную схему, соответствующую полученной таблице и введя два элемента задержки З1 и З2, получим структурную схему автомата (рис. 31).
7. Минимизация автоматов. С утилитарной точки зрения интерес представляет только зависимость между входами и выходами автомата, а роль его состоянии сводится исключительно к участию в формировании этих зависимостей в качестве промежуточных переменных. Следовательно, любая совокупность состояний, обеспечивающая требуемые зависимости между входом и выходом, может быть выбрана в качестве множества состоянии автомата. В то же время этот выбор естественно подчинить определенным целям, например, минимизации числа состояний или оптимизации автомата в каком-либо смысле. Следует иметь в виду, что с уменьшением числа состоянии уменьшается и количество требуемых элементов памяти, но это может привести к усложнению комбинационной схемы автомата. Поэтому синтез наиболее экономичного автомата часто требует поиска удачного компромисса между сложностью его комбинационной и запоминающих частей.

Рис. 32. Граф конечного автомата (а) и его сокращенная форма (б)
Минимизация числа состоянии полных автоматов связана с отношением эквивалентности. Пусть автоматы М1 и М2, находящиеся соответственно в начальных состояниях,  и
и  (обозначения М1 и М2 могут относиться к одному и тому же автомату), под воздействием любой входной последовательности выдают одинаковые выходные последовательности, т. е. автоматы М1 и М2 в данных состояниях
(обозначения М1 и М2 могут относиться к одному и тому же автомату), под воздействием любой входной последовательности выдают одинаковые выходные последовательности, т. е. автоматы М1 и М2 в данных состояниях  и
и  неразличимы по внешним выходам. Такое отношение между состояниями одного и того же или двух различных автоматов обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, оно является отношением эквивалентности состояний. Если состояния не эквивалентны, то их называют различимыми. Легко доказать справедливость следующих положений:
неразличимы по внешним выходам. Такое отношение между состояниями одного и того же или двух различных автоматов обладает свойствами рефлексивности, симметричности и транзитивности, следовательно, оно является отношением эквивалентности состояний. Если состояния не эквивалентны, то их называют различимыми. Легко доказать справедливость следующих положений:
1) состояния  и
и  автомата явно различимы, если различаются соответствующие, им строки в таблице выходов;
автомата явно различимы, если различаются соответствующие, им строки в таблице выходов;
2) состояния  и
и  автомата явно эквививалентны, если соответствующие им строки в таблице переходов и таблице выходов одинаковы или становятся одинаковыми при замене каждого номера
автомата явно эквививалентны, если соответствующие им строки в таблице переходов и таблице выходов одинаковы или становятся одинаковыми при замене каждого номера  на номер
на номер  (или наоборот).
(или наоборот).
Например, для автомата, граф которого изображен на рис. 32, а, общая таблица переходов имеет вид:
| x(v) s(v) | 0 | 1 | 2 |
| 0 | 1/1 | 4/0 | 4/1 |
| 1 | 5/1 | 1/1 | 4/1 |
| 2 | 1/0 | 1/1 | 6/1 |
| 3 | 3/1 | 2/0 | 0/1 |
| 4 | 1/1 | 4/0 | 4/1 |
| 5 | 1/0 | 5/1 | 4/1 |
| 6 | 5/0 | 5/1 | 2/1 |
Из этой таблицы следует, что состояния из множества {0, 3, 4}являются явно различимыми с любым состоянием из множества {1, 2, 5, 6}. Поэтому следует искать эквивалентные состояния только среди элементов, принадлежащих одному из этих множеств. Так как строки 0 и 4 одинаковы, а строки 1 и 5 становятся одинаковыми при замене цифры в числителе 1 на 5 (или 5 на 1), то явно эквивалентными являются пары состояний {0,4} И {1,5}.
Объединяя эквивалентные состояния в автомате М1, получаем эквивалентный автомат М2 с меньшим числом состоянии, который в любом состоянии нельзя отличить от исходного, наблюдая сигналы на выходах. Очевидно, автоматы М1 и М2 являются эквивалентными, если каждому состоянию  , автомата М1 соответствует, по крайней мере, одно эквивалентное ему состояние автомата M2, и если каждому состоянию
, автомата М1 соответствует, по крайней мере, одно эквивалентное ему состояние автомата M2, и если каждому состоянию  , автомата М2 соответствует хотя бы одно эквивалентное ему состояние автомата М1.
, автомата М2 соответствует хотя бы одно эквивалентное ему состояние автомата М1.
 |  |
Эквивалентные состояния, например,
 и
и  , удобно объединять по общей таблице переходов, вычеркивая строку
, удобно объединять по общей таблице переходов, вычеркивая строку  , и заменяя везде в числителе числа
, и заменяя везде в числителе числа  на
на  . После объединения пар явно эквивалентных состояний может оказаться возможным снова обнаружить такие состояния, которые также объединяются с помощью аналогичной процедуры. В результате последовательного объединения приходим к сокращенной таблице переходов, которой соответствует сокращенный автомат, эквивалентный исходному, но имеющий меньшее число состоянии. Так, для рассматриваемого примера получаем последовательно:
. После объединения пар явно эквивалентных состояний может оказаться возможным снова обнаружить такие состояния, которые также объединяются с помощью аналогичной процедуры. В результате последовательного объединения приходим к сокращенной таблице переходов, которой соответствует сокращенный автомат, эквивалентный исходному, но имеющий меньшее число состоянии. Так, для рассматриваемого примера получаем последовательно:
Первая таблица соответствует объединению пар эквивалентных состоянии {0,4} и {1, 5}, а вторая - объединению пары {2, 6}. Сокращенный автомат содержит только четыре состояния (рис.32, б).
Дата добавления: 2022-01-22; просмотров: 18; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!




