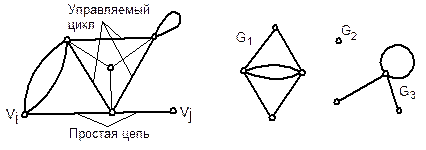Булевые функции двух переменных
Федеральное агентство по образованию
Тульский государственный университет
Кафедра «Автоматизированные станочные системы»
А.Б.Орлов
докт. техн. наук, профессор
ДИСКРЕТНАЯ МАТЕМТАИКА
КОНСПЕКТ ЛЕКЦИЙ
для студентов
направления 220 2 0 0
Тула 2005 г.
Введение. Предмет и метод дискретной математики.
Дискретная математика анализирует операции над переменными, возможные значения которых заданы на конечных множествах такие переменные называют дискретными или цифровыми. Подобные переменные могут быть, например, входными или выходными сигналами некоторой системы управления.
Задача управления любым объектом может быть поставлена следующим образом: Объект управления имеет на входе управляющие воздействия и входные материальные объекты и потоки (заготовки, потоки энергии и т.д.), а на выходе заданные материальные (готовые изделия) и информационные объекты. Часть выходных сигналов формируются информационными устройствами системы управления, связанными с объектом управления. Эти сигналы являются входными для системы управления, на выходе которой формируются управляющие воздействия.
Соответственно, системы управления делятся на две основные группы: непрерывные или аналоговые и дискретные или цифровые. Аналоговые системы управления характеризуются тем, что в них входные и выходные сигналы могут принимать любые значения из заданных диапазонов. При этом количество возможных значений этих сигналов бесконечно велико. Для цифровых систем управления входные и выходные сигналы могут принимать значения, принадлежащие к некоторым конечным множествам.
|
|
|
Рассмотрим, напрмер систему, имеющая n-входов (входных переменных), и m - выходов (выходных переменных), причем, входные и выходные переменные могут принимать значения из конечных множеств, которые называются - алфавитами.
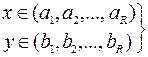 - алфавиты
- алфавиты
Возможные значения переменных, входящие во множества - алфавиты, называются буквами.
Конкретный набор значений входных, выходных переменных или переменных состояния называется слово. Различают входные и выходные слова Количество букв в слове (n, m или k) называют разрядностью слова.
Введем следующие обозначения:
X - входные слова;
Y - выходные слова;
Возможное количество слов зависит от размеров алфавита и разрядности слова. Это количество может быть определено, как:
Для входных слов - Rn
Для выходных слов - Qm
Наибольшее употребление в цифровых системах управления нашли двузначные (бинарные) или двоичные алфавиты. Причиной этого является максимальная помехозащищенность сигналов, передаваемых с помощью подобных алфавитов. Поэтому в дальнейшем будем рассматривать системы управления, имеющие только двузначные (бинарные) алфавиты. (0,1).
|
|
|
Для них
R=Q=2.
n=8, то 28=256
X0=0000000 - однобайтное входное слово;
X1=0000001 - однобайтное входное слово;
X255=11111111- однобайтное входное слово;
n, m и к - разрядности соответствующих слов;
m=3 то 23=8
y0=000;
y7=111;
к=2, то 22 =4
В процессе работы системы происходит преобразование последовательности входных слов в последовательности выходных.
Позиционные системы счисления.
В настоящее время в цифровых системах управления для кодирования переменных, адресов и команд находят применение следующие системы счисления: шестнадцатеричная, двоичная, восьмеричная и, естественно, десятичная системах счисления.
Изучение систем счисления относится к сфере дискретной математики, так как в основе каждой системы счисления лежит некоторое конечное дискретное множество цифр.
Все перечисленные выше системы счисления относятся к позиционным системам счисления, в которых доля, вносимая цифрой в число, зависит от ее позиции в числе. В любой позиционной системе счисления некоторое число, содержащее n цифр, может быть представлено как
|
|
|
xn xn-1 ...x2 x1 x0 = xn × an+xn-1 × an +...+x2 × a2 +x1 × a1 +x0 × a0
Здесь число а называют основанием системы счисления.
Например, в двоичной системе счисления:
10 a = 1 × a 1 +0 × a 0 = a
Легко показать, что в любой системе счисления число 10 равно основанию системы счисления а.
Двоичная система счисления не всегда хорошо читается человеком, поэтому при кодировании двоичные числа часто представляют шестнадцатеричными или восьмеричными числами, для которых возможен прямой перевод в двоичную систему счисления по тетрадам (четверкам) для шестнадцатеричной или триадам (тройкам) для восьмеричной системы счисления. Перевод шестнадцатеричных цифр в двоичные приведен в таблице.
| Десятичные числа | Шестнадцатеричные цифры | Двоичные числа | Восьмеричные числа | Двоично-десятичные числа |
| 0 | 0 | 0000 | 0 | 0000 |
| 1 | 1 | 0001 | 1 | 0001 |
| 2 | 2 | 0010 | 2 | 0010 |
| 3 | 3 | 0011 | 3 | 0011 |
| 4 | 4 | 0100 | 4 | 0100 |
| 5 | 5 | 0101 | 5 | 0101 |
| 6 | 6 | 0110 | 6 | 0110 |
| 7 | 7 | 0111 | 7 | 0111 |
| 8 | 8 | 1000 | 10 | 1000 |
| 9 | 9 | 1 00 1 | 11 | 1 00 1 |
| 10 | A | 1 0 1 0 | 12 | 0001 0 000 |
| 11 | B | 1 0 11 | 13 | 0001 000 1 |
| 12 | C | 11 00 | 14 | 0001 00 1 0 |
| 13 | D | 11 0 1 | 15 | 0001 00 11 |
| 14 | E | 111 0 | 16 | 0001 0 1 00 |
| 15 | F | 1111 | 17 | 0001 0 1 0 1 |
Рассмотрим простейшие арифметические действия в различных системах счисления.
|
|
|
Даны два шестнадцатеричных числа: В D +19
В D = В × 161+ D × 160=1110 × 16+1310=18910
1916= 1 × 161+9 × 160=2510
18910+2510=21410
21410=1310 × 16+6 = D 6
D + 9 = 1310 + 9 = 22, поскольку 22>15, требуется перенос в старший разряд
22 = 16 10 + 6 =1616
B + 1 + 1 = D
в результате получаем
| 1 | ||
| B | D | |
| + | 1 | 9 |
| D | 6 |
В двоичной системе счисления:
В = 10112
D= 11012
1 = 0001 2
9 = 1001 2
В D= 1011 11012
1 9 16 = 0001 1001 2
| 1 | 1 | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| + | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
11012 = D
01102 = 6
1101 01102 = D6
В восьмеричной системе счисления
В D= 1011 11012 = 0 10 _ 111 _ 1012
0 102 = 2
1112 = 7
1012 = 5
В D = 2758
1 9 16 = 0001 1001 2 = 0 00 _ 011 _ 001 2
0 00 2 = 0
011 2 = 3
001 2 = 1
1 9 16 = 318
2758 + 318
Осуществим поразрядное сложение
5 + 1 = 68
7 + 3 = 1010 , поскольку 10>7 требуется перенос в старший разряд
1010 = 810 + 2 = 128
2 + 1 = 38
В результате получим
| 1 | |||
| 2 | 7 | 5 | |
| + | 3 | 1 | |
| 3 | 2 | 6 |
2758 + 318 = 3268
Выполним проверку путем перевода в двоичную и шестнадцатеричную системы
счисления
38 = 0112
28 = 0102
68 = 1102
Отсюда получим
3268 = 011 _ 010 _ 1102 = 1101 _01102 = D 616
Достаточно широко используется также двоично-десятичная система счисления, в которой каждая десятичная цифра представляется двоичной тетерадой.
ОСНОВЫ ТЕОРИИ МНОЖЕСТВ
1. Что такое множество? Ответить на этот вопрос не так просто, как это кажется на первый взгляд. В повседневной жизни и практической деятельности часто приходится говорить о некоторых совокупностях различных объектов: предметов, понятий, чисел, символов и т. п. Например, совокупность деталей механизма, аксиом геометрии, чисел натурального ряда, букв русского алфавита. На основе интуитивных представлений о подобных совокупностях сформировалось математическое понятие множества как объединения отдельных объектов в единое целое. Именно такой точки зрения придерживался основатель теории множеств немецкий математик Георг Кантор.
Множество относится к категории наиболее общих, основополагающих понятий математики. Поэтому вместо строгого определения обычно принимается некоторое основное положение о множестве и его элементах. Так, группа выдающихся математиков, выступающая под псевдонимом Н. Бурбаки, исходит из следующего положения: «Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств».
2. Множество и его элементы. Утверждение, что множество А состоит из различимых элементов 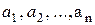 (и только из этих элементов), условно записывается
(и только из этих элементов), условно записывается  Принадлежность элемента множеству (отношение принадлежности) обозначается символом
Принадлежность элемента множеству (отношение принадлежности) обозначается символом 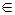 , т. е. a1
, т. е. a1  А, a2
А, a2  А, … , an
А, … , an  А, или короче
А, или короче 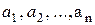
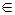 A. Если b не является элементом A, то пишут b
A. Если b не является элементом A, то пишут b  A или b
A или b 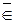 A.
A.
Два множества А и В равны (тождественны), А = В, тогда и только тогда, когда каждый элемент А является элементом В и обратно. Это значит, что множество однозначно определяется своими элементами.
Множество может содержать любое число элементов — конечное или бесконечное. Соответственно имеем конечные (множество цифр О, 1, ..., 9 или страниц в книге) или бесконечные (множество натуральных чисел или окружностей на плоскости) множества. Не следует, однако, связывать математическое понятие «множество» с обыденным представлением о множестве как о большом количестве. Так, единичное (одноэлементное) множество содержит только один элемент. Более того, вводится также понятие пустого множества, которое не содержит никаких элементов. Пустое множество обозначается специальным символом Ø.
Роль пустого множества Ø аналогична роли числа нуль. Это понятие можно использовать для определения заведомо несуществующей совокупности элементов (например, множество зеленых слонов, действительных корней уравнения х2+1=0). Более существенным мотивом введения пустого множества является то, что заранее не всегда известно (или неизвестно вовсе), существуют ли элементы, определяющие какое-то множество. Например, множество выигрышей в следующем тираже спортлото на купленные билеты может оказаться пустым. Никто еще не знает, является ли пустым или нет множество всех решений в целых числах уравнения х3 + у3 + z3 == 30. Без понятия пустого множества во всех подобных случаях, говоря о каком-нибудь множестве, приходилось бы
добавлять оговорку «если оно существует».
3. Множество и подмножества. Множество A, все элементы которого принадлежат и множеству В, называется подмножеством (частью) множества В. Это отношение между множествами называют включением и обозначают символом 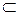 , т. е. А
, т. е. А 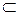 В (А включено в В) или В
В (А включено в В) или В  А (В включает А). Например, множество конденсаторов электронной цепи является подмножеством всех ее компонентов, множество положительных чисел — это подмножество множества действительных чисел.
А (В включает А). Например, множество конденсаторов электронной цепи является подмножеством всех ее компонентов, множество положительных чисел — это подмножество множества действительных чисел.
Отношение A  В допускает и тождественность (A=В), т. е. любое множество можно рассматривать как подмножество самого себя (A
В допускает и тождественность (A=В), т. е. любое множество можно рассматривать как подмножество самого себя (A  A). Полагают также, что подмножеством любого множества является пустое множество Ø, т. е. Ø
A). Полагают также, что подмножеством любого множества является пустое множество Ø, т. е. Ø  А. Одновременное выполнение соотношения A
А. Одновременное выполнение соотношения A  В и B
В и B  A возможно только при A=В. И обратно A=В, если A
A возможно только при A=В. И обратно A=В, если A  В и B
В и B  А. Это может служить определением равенства двух множеств через отношение включения.
А. Это может служить определением равенства двух множеств через отношение включения.
Наряду с A  В, в литературе можно встретить и другое обозначение A
В, в литературе можно встретить и другое обозначение A  В. При этом под A
В. При этом под A  В понимают такое отношение включения, которое не допускает равенства
В понимают такое отношение включения, которое не допускает равенства
A и В (строгое включение). Если допускается А=В, то пишут A  В (нестрогое включение). Мы будем придерживаться принятого ранее обозначения как для строгого, так и для нестрогого включения.
В (нестрогое включение). Мы будем придерживаться принятого ранее обозначения как для строгого, так и для нестрогого включения.
4. Множество подмножеств. Любое непустое множество А имеет, по крайней мере, два различных подмножества: само А и пустое множество Ø. Эти подмножества называются несобственными, а все другие подмножества А называют собственными (эта терминология связана со словами «собственно подмножества», а не со словом «собственность»). Конечные собственные подмножества образуются всевозможными сочетаниями по одному, два, три и т. д. элементов данного множества.
Элементы множества сами могут являться некоторыми множествами. Например, книга из множества книг в шкафу может рассматриваться как множество страниц. Здесь следует обратить внимание на то, что речь идет об элементах множества, а не о подмножествах (никакая совокупность страниц не может рассматриваться как подмножество множества книг).
Множество, элементами которого являются все подмножества множества А, называют множеством подмножеств (множеством-степенью) А и обозначают через Р(А). Так, для трехэлементного множества А={а, Ь, с} имеем Р(А)={ Ø, {а}, {b}, {c}, {а,b}, {а,c},{c,b},{а,b,c}}.
В случае конечного множества A, состоящего из n элементов, множество подмножеств Р(А) содержит 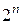 элементов. Доказательство основывается на сумме всех коэффициентов разложения бинома Ньютона или на представлении подмножеств n-раз- рядными двоичными числами, в которых 1 (или 0) соответствует элементам подмножеств.
элементов. Доказательство основывается на сумме всех коэффициентов разложения бинома Ньютона или на представлении подмножеств n-раз- рядными двоичными числами, в которых 1 (или 0) соответствует элементам подмножеств.
Следует подчеркнуть различия между отношением принадлежности и отношением включения. Как уже указывалось, множество A может быть своим подмножеством (A  A), но оно не может входить в состав своих элементов (A
A), но оно не может входить в состав своих элементов (A  A). Даже в случае одноэлементных подмножеств следует различать множество A={a} и его единственный элемент а. Отношение включения обладает свойством транзитивности: если A
A). Даже в случае одноэлементных подмножеств следует различать множество A={a} и его единственный элемент а. Отношение включения обладает свойством транзитивности: если A  B и B
B и B  C, то A
C, то A  C. Отношение принадлежности этим свойством не обладает. Например, множество A={1, {2,3} ,4} в числе своих элементов содержит множество {2, 3}, поэтому можно записать: 2,3
C. Отношение принадлежности этим свойством не обладает. Например, множество A={1, {2,3} ,4} в числе своих элементов содержит множество {2, 3}, поэтому можно записать: 2,3  {2, 3} и {2, 3}
{2, 3} и {2, 3} 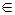 A. Но из этого вовсе не следует, что элементы 2 и 3 содержатся в A (в приведенном примере мы не находим 2 и 3 среди элементов множества A, т. е. 2, 3
A. Но из этого вовсе не следует, что элементы 2 и 3 содержатся в A (в приведенном примере мы не находим 2 и 3 среди элементов множества A, т. е. 2, 3 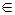 A.
A.
5. Задание множеств. Множество 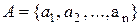 можно задать простым перечислением его элементов. Например, спецификация задает множество деталей изделия, каталог — множество книг в библиотеке. Но этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств часто практически нереализуем.
можно задать простым перечислением его элементов. Например, спецификация задает множество деталей изделия, каталог — множество книг в библиотеке. Но этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств часто практически нереализуем.
Рассмотрим в качестве примера фасад 16-этажного дома с 38 окнами в каждом этаже. В вечернее время каждое из окон дома может быть освещено или затемнено, т. е. находиться в двух состояниях. Определенные совокупности освещенных окон можно рассматривать как некоторые образы. Считая все окна (их число равно 38*16=608) различными по их расположению на фасаде, каждый такой образ можно связать с соответствующим подмножеством освещенных окон. Тогда количество всех образов равно количеству элементов множества подмножеств всех окон, т. е. 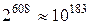 . Полученное число настолько большое, что его трудно даже представить. Оно несравнимо больше числа атомов во всей видимой вселенной, которое равно примерно 1037. Если бы каждый атом превратился во вселенную, то и тогда на один атом приходилось бы 1037 образов 10183 == 1073 *1073 * 1037). Поэтому, хотя множество всех образов конечно и любой из них можно легко определить, о задании подобных множеств перечислением их элементов не может быть и речи.
. Полученное число настолько большое, что его трудно даже представить. Оно несравнимо больше числа атомов во всей видимой вселенной, которое равно примерно 1037. Если бы каждый атом превратился во вселенную, то и тогда на один атом приходилось бы 1037 образов 10183 == 1073 *1073 * 1037). Поэтому, хотя множество всех образов конечно и любой из них можно легко определить, о задании подобных множеств перечислением их элементов не может быть и речи.
6. Определяющее свойство. Другой способ задания множества состоит в описании элементов определяющим свойством Р(х) (формой от х), общим для всех элементов. Обычно Р(х) — это высказывание, в котором что-то утверждается об х, или некоторая функция переменной х. Если при замене х на а высказывание Р(а) становится истинным или функция в заданной области определения удовлетворяется, то а есть элемент данного множества. Множество, заданное с помощью формы Р(х), обозначается как Х={х | Р(х)}, или Х={х :Р(х)}, причем а 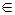 {х | Р(х)}, если Р(а) истинно. Например {х | х2 = 2} - множество чисел, квадрат которых равен двум, {х | х есть животное с хоботом} - множество слонов.
{х | Р(х)}, если Р(а) истинно. Например {х | х2 = 2} - множество чисел, квадрат которых равен двум, {х | х есть животное с хоботом} - множество слонов.
Обычно уже в самом определении конкретного множества явно или неявно ограничивается совокупность допустимых объектов. Так, множество слонов следует искать среди млекопитающих, а не среди рыб и тем более не среди планет. Если речь идет о множестве чисел, делящихся на 3, то ясно, что оно является подмножеством целых чисел. Удобно совокупность допустимых объектов зафиксировать явным образом и считать, что рассматриваемые множества являются подмножествами этой совокупности. Ее называют основным множеством (универсумом) и обычно обозначают через И. Так, универсумом арифметики служат числа, зоологии - мир животных, лингвистики - слова и т.п.
Если множество выделяется из множества A с помощью формы Р(х), то запись
{х | х 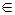 А, Р(х)} часто упрощается: {х
А, Р(х)} часто упрощается: {х 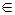 А | Р(х)}. Запись f(х) | Р(х)} означает множество всех таких у=f(х), для которых имеется х, обладающий свойством Р(х). Например, {х2 | х - простое число} означает множество квадратов простых чисел.
А | Р(х)}. Запись f(х) | Р(х)} означает множество всех таких у=f(х), для которых имеется х, обладающий свойством Р(х). Например, {х2 | х - простое число} означает множество квадратов простых чисел.
7. Операции над множествами. Множества можно определять также при помощи операций над некоторыми другими множествами. Пусть имеются два множества A и B.
Объединение (сумма) А 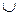 В есть множество всех элементов, принадлежащих A или В. Например, {1, 2, 3}
В есть множество всех элементов, принадлежащих A или В. Например, {1, 2, 3}  (2, 3, 4} = {1, 2, 3, 4}.
(2, 3, 4} = {1, 2, 3, 4}.
Пересечение (произведение) А  В есть множество всех элементов, принадлежащих одновременно как A, так и В. Например, {1, 2, 3}
В есть множество всех элементов, принадлежащих одновременно как A, так и В. Например, {1, 2, 3}  {2, 3, 4} = {2, 3}. Множества, не имеющие общих элементов (A
{2, 3, 4} = {2, 3}. Множества, не имеющие общих элементов (A  В = Ø), называют непересекающимися (расчлененными).
В = Ø), называют непересекающимися (расчлененными).
Разность А \ В (или A - В) есть множество, состоящее из всех элементов A, не входящих в В, например, {1, 2, 3} \ {2, 3, 4} = {1}. Ее можно рассматривать как относительное дополнение В до A. Если A  U, то множество U \ A называется абсолютным дополнением (или просто дополнением) множества A и обозначается через A. Оно содержит все элементы универсума U, кроме элементов множества A. Дополнение A определяется отрицанием свойства Р(х), с помощью которого определяется A. Очевидно, А \ В = A
U, то множество U \ A называется абсолютным дополнением (или просто дополнением) множества A и обозначается через A. Оно содержит все элементы универсума U, кроме элементов множества A. Дополнение A определяется отрицанием свойства Р(х), с помощью которого определяется A. Очевидно, А \ В = A  В.
В.
Дизъюнктивная сумма (симметрическая разность) А + В (или A  В) есть множество всех элементов, принадлежащих или A, или В (но не обоим вместе). Например, {1, 2, 3} + {2, 3, 4} = {1, 4}. Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.
В) есть множество всех элементов, принадлежащих или A, или В (но не обоим вместе). Например, {1, 2, 3} + {2, 3, 4} = {1, 4}. Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.
8. Круги Эйлера. Для наглядного изображения соотношений между подмножествами какого-либо универсума и используют круги Эйлера (рис. 1). Обычно универсум представляется множеством точек прямоугольника, а его подмножества изображаются в виде кругов или других простых областей внутри этого прямоугольника.
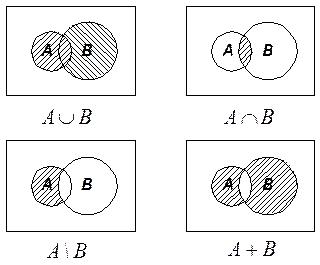
| Рис. 1. Круги Эйлера для основных операций над множествами. |
Множества, получаемые в результате операций над множествами A и В, изображены на рис. 1 заштрихованными областями. Непересекающиеся множества
изображаются неперекрывающимися областями, а включение множества соответствует области, целиком располагающейся внутри другой (рис. 2). Дополнение множества A (до U), т. е. множество  изображается той частью прямоугольника, которая лежит за пределами круга, изображающего A.
изображается той частью прямоугольника, которая лежит за пределами круга, изображающего A.
9. Отношения. В начале этого параграфа речь шла о том, что элементы множества могут находиться в некоторых отношениях между собой или с элементами других множеств.
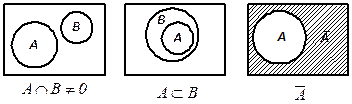
| 2. Круги Эйлера для непересекающихся множеств, отношения включения и дополнения. |
В самом общем смысле отношение означает какую-либо связь между предметами или понятиями. Отношения между парами объектов называют бинарными (двуместными). Выше же были рассмотрены два таких отношения - принадлежность (а 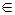 A) и включение A
A) и включение A  B. Первое из них определяет связь между множеством и его элементами, а второе - между двумя множествами. Примерами бинарных отношений являются равенство (=), неравенства (< или
B. Первое из них определяет связь между множеством и его элементами, а второе - между двумя множествами. Примерами бинарных отношений являются равенство (=), неравенства (< или  ), а также такие выражения как «быть братом», «делиться (на какое-то число)», «входить в состав (чего-либо)» и т. п.
), а также такие выражения как «быть братом», «делиться (на какое-то число)», «входить в состав (чего-либо)» и т. п.
Для любого бинарного отношения можно записать соответствующее ему соотношение (для отношения неравенства соотношением будет х < у, для отношения «быть братом» соотношение запишется как «х брат у»). В общем виде соотношение можно записать как хАу, где А - отношение, устанавливающее связь между элементом х из множества
Х (х  X) и элементом y из множества Y (y
X) и элементом y из множества Y (y  Y). Ясно, что отношение полностью определяется множеством всех пар элементов (х, у), для которых оно имеет место. Поэтому любое бинарное отношение А можно рассматривать как множество упорядоченных пар (х, у).
Y). Ясно, что отношение полностью определяется множеством всех пар элементов (х, у), для которых оно имеет место. Поэтому любое бинарное отношение А можно рассматривать как множество упорядоченных пар (х, у).
Отношения могут обладать некоторыми общими свойствами (например, отношение включения и отношение равенства транзитивны). Определяя эти свойства и комбинируя их, можно выделить важные типы отношений, изучение которых в общем виде заменяет рассмотрение огромного множества частных отношений.
10. Функции как отношения. Функция f, ставящая каждому числу х (аргументу) в соответствие определенное число (значение функции) у=f(х), также является бинарным отношением.
Обобщая это понятие, можно считать функцией такое бинарное отношение f, которое каждому элементу х из множества Х ставит в соответствие один и только один элемент из множества Y, т. е. хfу. При этом считают, что элементами множеств Х и Y могут быть объекты любой природы, а не только числа.
Функцией в таком общем понимании будет, например, соответствие между деталями какого-либо механизма и их массой (каждой детали соответствует ее масса), между человеком и его фамилией и т. п. В то же время такие отношения как неравенство (<) или «быть братом» функциями не являются, так как для каждого числа можно указать бесконечные множества превышающих его чисел, а человек может иметь несколько братьев или совсем их не иметь.
Обобщение понятия функции явилось одним из отправных моментов нового важного раздела современной математики - функционального анализа. Это понятие имеет огромное прикладное значение, так как позволяет рассматривать функциональные отношения между объектами любой природы.
ОСНОВЫ ТЕОРИИ ГРАФОВ
1. Происхождение графов. Многие задачи сводятся к рассмотрению совокупности объектов, существенные свойства которых описываются связями между ними. Например, глядя на карту автомобильных дорог, можно интересоваться только тем, имеется ли связь между некоторыми населенными пунктами, отвлекаясь от конфигурации и качества дорог, расстояний и других подробностей. При изучении электрических цепей на первый план может выступать характер соединений различных ее компонентов - резисторов, конденсаторов, источников и т. п. Органические молекулы образуют структуры, характерными свойствами которых являются связи между атомами. Интерес могут представлять различные связи и отношения между людьми, событиями, состояниями и вообще между любыми объектами.

| Рис. 3. К задаче о кенигсбергских мостах: а — план города; б — граф. |
В подобных случаях удобно рассматриваемые объекты изображать точками, называемыми вершинами, а связи между ними - линиями (произвольной конфигурации), называемыми ребрами. Множество вершин V, связи между которыми определены множеством ребер Е, называют графом и обозначают 0 = (V, Е). Первая работа по графам была опубликована двадцатилетним Леонардом Эйлером в 1736 г., когда он работал в Российской Академии наук. Она содержала решение задачи о кенигсбергских мостах
(рис. 3, а): можно ли совершить прогулку таким образом, чтобы выйдя из любого места города, вернуться в него, пройдя в точности один раз по каждому мосту? Ясно, что по условию задачи не имеет значения, как проходит путь по частям суши а, b, с, d, на которых расположен г. Кенигсберг (ныне Калининград), поэтому их можно представить вершинами. А так как связи между этими частями осуществляются только через семь мостов, то каждый из них изображается ребром, соединяющим соответствующие вершины. В результате получаем граф, изображенный на рис. 3, б. Эйлер дал отрицательный ответ на поставленный вопрос. Более того, он доказал, что подобный маршрут имеется только для такого графа, каждая из вершин которого связана с четным числом ребер.
С тех пор поток задач с применением графов нарастал подобно снежной лавине. Наряду с многочисленными головоломками и игграми на графах, рассматривались важные практические проблемы, многие из которых требовали тонких математических методов. Уже в середине прошлого века Кирхгоф применил графы для анализа электрических цепей, а Кэли исследовал важный класс графов для выявления и перечисления изомеров насыщенных углеводородов.
Однако теория графов как математическая дисциплина сформировалась только к середине тридцатых годов нашего столетия благодаря работам многих исследователей, наибольшая заслуга среди которых принадлежит Д. Кенигу. Значительный вклад в теорию графов внесли советские ученые Л. С. Понтрягин, А. А. Зыкоз, В. Г. Визинг и др.
Теория графов располагает мощным аппаратом решения прикладных задач из самых различных областей науки и техники. Сюда относятся, например, анализ и синтез цепей и систем, проектирование каналов связи и исследование процессов передачи информации, построение контактных схем и исследование конечных автоматов, сетевое планирование и управление, исследование операций, выбор оптимальных маршрутов и потоков в сетях, моделирование жизнедеятельности и нервной системы живых организмов, исследование случайных процессов и многие другие задачи. Теория графов тесно связана с такими разделами математики, как теория множеств, теория матриц, математическая логика и теория вероятностей. Во всех этих разделах графы применяют для представления различных математических объектов, и в то же время сама теория графов широко использует аппарат родственных разделов математики.
2. Ориентированные графы. Часто связи между объектами характеризуются вполне определенной ориентацией. Например, на некоторых улицах допускается только одностороннее автомобильное движение, в соединительных проводах электрической цепи задаются положительные направления токов, отношения между людьми могут определяться подчиненностью или старшинством. Ориентированные связи характеризуют переход системы из одного состояния в другое, результаты встреч между командами в спортивных состязаниях, различные отношения между числами (неравенство, делимость).
Для указания направления связи между вершинами графа соответствующее ребро отмечается стрелкой. Ориентированное таким образом ребро называют дугой, а граф с ориентированными ребрами - ориентированным графом или короче орграфом (рис. 4, а).
Если пара вершин соединяется двумя или большим числом дуг, то такие дуги называют параллельными. При этом две дуги, одинаково направленные по отношению к данной вершине, называют строго параллельными, а различно направленные — нестрого параллельными. Ясно, что нестрого параллельные дуги, отображающие ориентацию связи в обоих направлениях, по существу равноценны неориентированной связи и могут быть заменены ребром. Произведя такую замену в орграфе, придем к смешанному графу, который содержит ребра н дуги (рис. 4, б). Обратно, любой неориентированный или смешанный граф можно преобразовать в ориентированный заменой каждого ребра парой нестрого параллельных дуг.
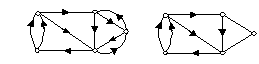
| Рис. 4. Ориентированный (а) и смешанный(б) графы. |
Изменив направления всех дуг орграфа на противоположные, получаем орграф, обратный исходному. Если направления дуг орграфа не учитываются и каждая дуга рассматривается как неориентированное ребро, то он называется соотнесенным (неориентированным) графом.
3. Взвешенные графы. Дальнейшее обобщение отображения связей между объектами с помощью графов состоит в приписывании ребрам и дугам некоторых количественных значений, качественных признаков или характерных свойств, называемых весами.
В простейшем случае это может быть порядковая нумерация ребер и дуг, указывающая на очередность при их рассмотрении (приоритет или иерархия). Вес ребра или дуги может означать длину (пути сообщения), пропускную способность (линии связи), напряжение или ток (электрические цепи), количество набранных очков (турниры), валентность связей (химические формулы), количество рядов движения (автомобильные дороги), цвет проводника (монтажная схема электронного устройства), характер отношений между людьми (сын, брат, отец, подчиненный, учитель) и т. п.
Вес можно приписывать не только ребрам и дугам, но и вершинам. Например, вершины, соответствующие населенным пунктам на карте автомобильных дорог, могут характеризоваться количеством мест в кемпингах, пропускной способностью станций техобслуживания. Вообще, вес вершины означает любую характеристику соответствующего ей объекта (атомный вес элемента в структурной формуле, цвет изображаемого вершиной предмета, возраст человека и т. п.).
Особое значение для моделирования физических систем приобрели взвешенные ориентированные графы, названные графами потоков сигналов или сигнальными графами. Вершины сигнального графа отождествляются с некоторыми переменными, характеризующими состояние системы, а вес каждой вершины означает функцию времени или некоторые величины, характеризующие соответствующую переменную (сигнал вершины). Дуги отображают связи между переменными, и вес каждой дуги представляет собой численное или функциональное отношение, характеризующее передачу сигнала от одной вершины к другой (передача дуги). Сигнальные графы находят широкое применение в теории цепей и систем, а также во многих других областях науки и техники.
4. Типы конечных графов. Если множество вершин графа конечно, то он называется конечным графом. В математике рассматриваются и бесконечные графы, но мы заниматься ими не будем, так как в практических приложениях они встречаются редко. Конечный граф G = (V, E), содержащий р вершин и q ребер, называется (р, q)-графом.
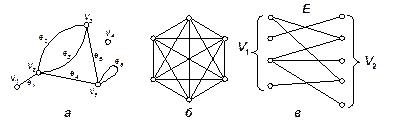
| Рис. 5. Типы графов: а - псевдограф; б - полный граф (шестиугольник); в - двудольный граф (биграф). |
Пусть V = {  } и E = {
} и E = { 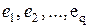 } - соответственно множества вершин и ребер (р, q)-графа. Каждое ребро
} - соответственно множества вершин и ребер (р, q)-графа. Каждое ребро 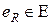 соединяет пару вершин
соединяет пару вершин 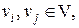 являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. Ребра с одинаковыми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вершины, которые не являются концами ребер и не связаны ни между собой, ни с другими вершинами. Например, для (5, 6)-графа на рис. 5, а V={
являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. Ребра с одинаковыми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вершины, которые не являются концами ребер и не связаны ни между собой, ни с другими вершинами. Например, для (5, 6)-графа на рис. 5, а V={ 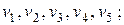 }; Е=
}; Е= 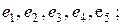 ребра
ребра  и
и 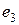 параллельны, ребро
параллельны, ребро 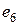 является петлей, а
является петлей, а 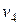 - изолированная вершина.
- изолированная вершина.
Число ребер, связанных с вершиной 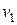 (петля учитывается дважды), называют степенью вершины и обозначают через
(петля учитывается дважды), называют степенью вершины и обозначают через 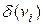 или deg
или deg 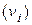 . Так, для графа на рис. 5, а
. Так, для графа на рис. 5, а  =1,
=1, 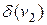 = 4 и т. д. Очевидно, степень изолированной вершины равна нулю
= 4 и т. д. Очевидно, степень изолированной вершины равна нулю
(  = 0). Вершина степени единицы называется концевой или висячей вершиной (
= 0). Вершина степени единицы называется концевой или висячей вершиной (  =1). Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные
=1). Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные 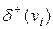 и отрицательные
и отрицательные 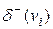 степени вершин, которые равны соответственно числу исходящих из
степени вершин, которые равны соответственно числу исходящих из 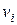 и заходящих в
и заходящих в 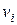 дуг. Например, для вершины d орграфа (см. рис. 5, а) имеем
дуг. Например, для вершины d орграфа (см. рис. 5, а) имеем 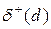 = 2 и
= 2 и 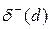 = 3. Очевидно, суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.
= 3. Очевидно, суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.
Граф без петель и кратных ребер называют простым или обыкновенным. Граф без петель, но с кратными ребрами называют мультиграфом. Наиболее общий случай графа, когда допускаются петли и кратные ребра, называют псевдографом. Так, граф на рис. 4,б - это мультиграф, а на рис. 5, а - псевдограф. Если граф не имеет ребер (Е = Ø), то все его вершины изолированы (V 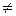 Ø), и он называется пустым или нульграфом. Простой граф, в котором любые две вершины соединены ребром, называется полным (на рис. 5, б приведен пример полного графа с шестью вершинами). Если множество вершин V простого графа допускает такое разбиение на два непересекающихся подмножества V1 и V2 (V1
Ø), и он называется пустым или нульграфом. Простой граф, в котором любые две вершины соединены ребром, называется полным (на рис. 5, б приведен пример полного графа с шестью вершинами). Если множество вершин V простого графа допускает такое разбиение на два непересекающихся подмножества V1 и V2 (V1  V2
V2 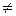 Ø ), что не существует ребер, соединяющих вершины одного и того же подмножества, то он называется двудольным или биграфом (рис. 5, б). Ориентированный граф считается простым, если он не имеет строго параллельных дуг и петель.
Ø ), что не существует ребер, соединяющих вершины одного и того же подмножества, то он называется двудольным или биграфом (рис. 5, б). Ориентированный граф считается простым, если он не имеет строго параллельных дуг и петель.
Граф, степени всех вершин которого одинаковы и равны г, называется однородным (регулярным) r-й степени. Полный граф с n вершинами всегда однородный степени n-1, а пустой граф-однородный степени 0. Граф третьей степени называют кубическим. Он обладает рядом интересных свойств и, в частности, всегда имеет четное число вершин.
5. Смежность. Две вершины 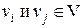 графа G = (V, Е) называются смежными, если они являются граничными вершинами ребра
графа G = (V, Е) называются смежными, если они являются граничными вершинами ребра 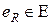 . Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т. е.
. Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т. е.  R = 1, 2, …, q. Для неориентированных графов такие пары неупорядочены, так что
R = 1, 2, …, q. Для неориентированных графов такие пары неупорядочены, так что 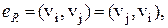 а для орграфов — упорядочены, причем и,
а для орграфов — упорядочены, причем и, 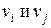 означают соответственно начальную и конечную вершины дуги
означают соответственно начальную и конечную вершины дуги  . Петля при вершине
. Петля при вершине 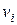 , в обоих случаях представляется неупорядоченной парой
, в обоих случаях представляется неупорядоченной парой 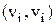 . Ясно, что множество вершин V вместе с определенным на нем отношением смежности полностью определяет граф.
. Ясно, что множество вершин V вместе с определенным на нем отношением смежности полностью определяет граф.
Граф можно представить также матрицей смежности. Строки и столбцы этой матрицы соответствуют вершинам графа, а ее (ij) - элемент равен числу кратных ребер, связывающих вершины 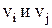 , (или направленных от вершины vi к вершине vj, для орграфа). Например, для графов, приведенных на рис. 4, а и 5, а, имеем соответственно следующие матрицы смежности:
, (или направленных от вершины vi к вершине vj, для орграфа). Например, для графов, приведенных на рис. 4, а и 5, а, имеем соответственно следующие матрицы смежности:
| V1= | a | b | C | d | e | V2= | v1 | v2 | v3 | v4 | v5 | ||
| 1 | 1 | a | 1 | v1 | |||||||||
| 1 | 1 | b | 1 | 2 | 1 | v2 | |||||||
| 1 | 1 | c; | 2 | 1 | v3. | ||||||||
| 1 | 1 | d | v4 | ||||||||||
| 2 | e | 1 | 1 | 1 | v5 |
Матрица смежности неориентированного графа всегда симметрична а орграфа - в общем случае несимметрична. Неориентированным ребрам соответствуют пары ненулевых элементов, симметричных относительно главной диагонали матрицы, дугам - ненулевые элементы матрицы, а петлям - ненулевые элементы главной диагонали. В столбцах и строках, соответствующих изолированным вершинам, все элементы равны нулю. Элементы матрицы простого графа равны 0 или 1, причем все элементы главной диагонали нулевые.
Для взвешенного графа, не содержащего кратных ребер, можно обобщить матрицу смежности так, что каждый ее ненулевой элемент равняется весу соответствующего ребра или дуги. Обратно, любая квадратная матрица n-го порядка может быть представлена орграфом с n вершинами, дуги которого соединяют смежные вершины и имеют веса, равные соответствующим элементам матрицы. Если матрица симметрична, то она представима неориентированным графом.
6. Инцидентность. Если вершина vi, является концом ребра eR то говорят, что они инцидентны: вершина vi инцидентна ребру eR и ребро eR, инцидентно вершине vi. В то время как смежность представляет собой отношение между однородными объектами (вершинами), инцидентность — это отношение между разнородными объектами (вершинами и ребрами). При рассмотрении орграфов различают положительную инцидентность (дуга исходит из вершины) и отрицательную инцидентность (дуга заходит в вершину).
Рассматривая инцидентность вершин и ребер (p и q) - графа, можно представить его матрицей инцидентности размера p x q, строки которой соответствуют вершинам, а столбы - ребрам. Для неориентированного графа элементы этой матрицы определяются по следующему правилу: ij-элемент равен 1, если вершина vi, инцидентна ребру ei, и равен нулю, если vi, и ei, не инцидентны. В случае орграфа ненулевой ij-элемент равен 1, если vi начальная вершина дуги ei, и равен - 1, если vi - конечная вершина дуги ei.
Например, матрица инцидентности графа, приведенного на рис. 5, а, имеет вид:
| A= | e1 | e2 | e3 | e4 | e5 | e6 | |
| 1 | v1 | ||||||
| 1 | 1 | 1 | 1 | v2 | |||
| 1 | 1 | 1 | v3. | ||||
| v4 | |||||||
| 1 | 1 | v5 |
Каждый столбец матрицы инцидентности содержит обязательно два единичных элемента (для орграфа эти элементы всегда имеют различные знаки и равны соответственно 1 и —1). Количество единиц в строке равно степени соответствующей вершины (для орграфа количество положительных единиц определяет положительную степень, а количество отрицательных единиц — отрицательную степень). Нулевая строка соответствует изолированной вершине, а нулевой столбец - петле.

| Рис. 6. Изоморфные графы |
Следует иметь в виду, что нулевой столбец матрицы инцидентности лишь указывает на наличие петли, но не содержит сведений о том, с какой вершиной эта петля связана (в практических приложениях это может быть несущественно).
7. Изоморфизм. На рис. 6 изображены три графа, которые с геочетрической точки зрения совершенно различны (пересечение ребер, если оно не отмечено точкой, не является вершиной). Но по существу они различаются лишь начертанием, а отношения инцидентности (при соответствующем обозначении вершин и ребер) для них одинаковы. Графы, для которых сохраняется отношение инцидентности, называются изоморфными.
Ясно, что матрица инцидентности определяет граф без петель с точностью до изоморфизма. Обычно на ее основе можно изобразить различные в геометрическом отношении, но изоморфные между собой графы, каждый из которых называют геометрической реализацией. Графы, которые имеют одинаковые начертания и отличаются лишь нумерацией вершин и ребер, не будучи тождественными, являются изоморфными.
Если существенные свойства графа не связаны со способом его изображения на плоскости или нумерацией вершин и ребер, то изоморфные графы, как правило, не различают между собой.
8. Маршруты. Нередко задачи на графах требуют выделения различных маршрутов, обладающих определенными свойствами и характеристиками. Маршрут длины m определяется как последовательность т ребер графа (не обязательно различных) таких, что граничные вершины двух соседних ребер совпадают. Маршрут проходит и через все вершины, инцидентные входящим в него ребрам. Примерами маршрутов на графе рис. 5, а могут служить последовательности ( 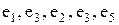 ), (
), ( 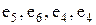 ). Первый маршрут проходит через последовательность вершин (
). Первый маршрут проходит через последовательность вершин ( 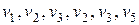 ) и соединяет вершины
) и соединяет вершины  и
и 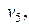 a второй — через последовательность вершин (
a второй — через последовательность вершин ( 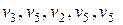 ) и соединяет вершины
) и соединяет вершины 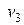 и
и  . Замкнутый маршрут приводит в ту же вершину, из которой он начался.
. Замкнутый маршрут приводит в ту же вершину, из которой он начался.
Маршрут, все ребра которого различны, называется цепью, а маршрут, для которого различны все вершины, называется простой цепью. Замкнутая цепь называется циклом, а простая цепь - простым циклом. Так, на графе рис. 5, а ( 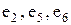 ) - цепь, (
) - цепь, ( 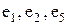 ) -простая цепь, (
) -простая цепь, ( 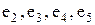 ) - цикл, (
) - цикл, ( 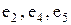 ) - простой цикл.
) - простой цикл.
Цикл, который содержит все ребра графа, называется эйлеровым циклом (задача о кенигсбергских мостах сводится к выяснению существования такого цикла), а граф, в котором имеется такой цикл, называется эйлеровым графом. Простой цикл, который проходит через все вершины графа, называют гамильтоновым. Если критерий существования эйлерового цикла очень прост (необходимо, чтобы степени всех вершин были четными), то для гамильтоновых циклов никакого общего правила не найдено.
Ориентированные маршруты на орграфе определяются аналогично с той разницей, что начальная вершина каждой последующей дуги маршрута должна совпадать с конечной вершиной предыдущей дуги. Иначе говоря, движение по маршруту допускается только в направлениях, указанных стрелками. Маршрут, не содержащий повторяющихся дуг, называется путем, а не содержащий повторяющихся вершин - простым путем. Замкнутый путь называется контуром, а простой замкнутый путь - простым контуром. Граф (орграф) называется циклическим (контурным), если он содержит хотя бы один цикл (контур), в противном случае он называется ациклическим (бесконтурным).
Понятия цепи и цикла применимы и к ориентированным графам. При этом направления дуг не учитываются, т. е. по существу вместо орграфа рассматривают неориентированный соотнесенный ему граф.
9. Части графа. Граф G' = (V', Е') является частью графа G = (V, Е), если V' 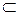 V и Е'
V и Е' 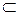 Е, т. е. граф содержит все вершины и ребра любой его части. Часть, которая, наряду с некоторым подмножеством ребер графа, содержит и все инцидентные им вершины, называется подграфом. Часть, которая наряду с некоторым подмножеством ребер графа, содержит все вершины графа (V’=V, Е'
Е, т. е. граф содержит все вершины и ребра любой его части. Часть, которая, наряду с некоторым подмножеством ребер графа, содержит и все инцидентные им вершины, называется подграфом. Часть, которая наряду с некоторым подмножеством ребер графа, содержит все вершины графа (V’=V, Е' 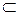 Е), называется суграфом. Рассмотренные графы показаны на рис. 7.
Е), называется суграфом. Рассмотренные графы показаны на рис. 7.

| Рис. 7. Граф и его части: а - граф; б - часть графа; в - подграф; г – суграф. |
Исходный граф по отношению к его подграфу называют надграфом, а по отношению к суграфу - сверхграфом. Совокупность всех ребер графа, не принадлежащих его подграфу (вместе с инцидентными вершинами), образует дополнение подграфа. Говорят, что подграфы G' = (V', Е') и G" = (V", Е") разделены ребрами, если они не имеют общих ребер (Е'  Е" =Ø) и разделены вершинами, если у них нет общих вершин (V'
Е" =Ø) и разделены вершинами, если у них нет общих вершин (V'  V" =Ø).
V" =Ø).
10. Связность. Две вершины графа называют связанными, если существует маршрут, соединяющий эти вершины. Граф, любая пара вершин которого связана, называют связным графом. Очевидно, в связном графе между любыми двумя вершинами существует простая цепь, так как из связывающего их маршрута всегда можно удалить циклический участок, проходящий через некоторую вершину более одного раза (рис. 8, где маршрут между вершинами 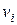 и
и 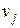 , изображен жирными линиями).
, изображен жирными линиями).
Если граф не связный, то множество его вершин можно единственным образом разделить на непересекающиеся подмножества, каждое из которых содержит все связанные между собой вершины и вместе с инцидентными им ребрами образует связный подграф. Таким образом, несвязный граф представляет собой совокупность отдельных частей (подграфов), называемых компонентами. На рис. 9 показан подграф, состоящий из трех компонент (изолированная вершина считается компонентой).
Часто отношение связности усложняется дополнительными условиями. Граф называют циклически связным, если любые две различные вершины содержатся в цикле (например, граф на рис. 7, а циклически связный, а граф на рис. 8 - нет, так как вершина и, не содержится ни в каком цикле с другими вершинами). Граф называют R - связным, если любая пара различных вершин связана, по крайней мере R цепями, которые не имеют общих вершин (кроме начальной и конечной). Так, граф на рис. 7, а двусвязный, а на рис. 8 - односвязный.
|
| |
| Простая Цепь Рис. 8. Связный граф. | Рис. 9. Несвязный граф, состоящий из трех компонент (G1, G2, G3) |
Связность ориентированных графов определяется так же, как и для неориентированных (без учета направлений дуг). Специфичным для орграфа (или смешанного графа) является понятие сильной связности. Орграф называют сильно связным, если для любой пары его вершин 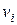 и
и 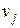 существует путь из
существует путь из 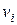 в
в 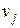 и из
и из 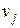 в
в 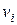 , (например, граф на рис. 4, а сильно связный). Граф, представляющий план города с односторонним движением по некоторым улицам, должен быть сильно связным, так как в противном случае нашлись бы вершины (площади и перекрестки), между которыми нельзя было бы проехать по городу без нарушения правил движения.
, (например, граф на рис. 4, а сильно связный). Граф, представляющий план города с односторонним движением по некоторым улицам, должен быть сильно связным, так как в противном случае нашлись бы вершины (площади и перекрестки), между которыми нельзя было бы проехать по городу без нарушения правил движения.
11. Разделимость. Связный граф может быть разделен на несвязные подграфы удалением из него некоторых вершин и ребер (при удалении вершин исключаются и все инцидентные им ребра, а при удалении ребер вершины сохраняются). Если существует такая вершина, удаление которой превращает связный граф (или компоненту несвязного графа) в несвязный, то она называется точкой сочленения (рис. 10, а). Ребро с такими же свойствами называется мостом (рис. 10, б). Ясно, что при наличии моста в графе имеется, по крайней мере, две точки сочленения.
Граф называется неразделимым, если он связный и не имеет точек сочленения (например, граф на рис. 7, а неразделим). Граф, имеющий хотя бы одну точку сочленения, является разделимым и называется сепарабельным. Он разбивается на блоки, каждый из котооых представляет собой максимальный неразделимый подграф (на рис. 10, в показаны блоки B1,B2,B3 графа рис. 10, б).
Каждое ребро графа, как и каждая вершина (за исключением точек сочленения), принадлежат только одному из его блоков. Более того, только одному блоку принадлежит и каждый простой цикл. Отсюда следует, что совокупность блоков графа представляет собой разбиение множеств ребер и простых циклов на непересекающиеся подмножества.

|
| Рис. 10. Разделимые графы: а - с точкой сочленения; б - с мостом; в - блоки B1 - B3 графа с мостом |
В ряде приложений теории графов блоки можно рассматривать как компоненты. Это обычно допустимо, когда связи блоков посредством точки сочленения несущественны или когда существенные свойства графа связаны только с его простыми циклами (контурами). В таких случаях можно рассматривать несвязный граф как связный разделимый граф, который образуется путем такого объединения компонент, чтобы каждая из них была блоком (это всегда можно сделать, объединив, например, по одной вершине каждого блока в точку сочленения). Подобные операции используются при рассмотрении графов электрических цепей.
12. Деревья и лес. Особый интерес представляют связные ациклические графы, называемые деревьями. Дерево на множестве р вершин всегда содержит q = р - 1 ребер, т. е. минимальное количество ребер, необходимое для того, чтобы граф был связным. Действительно, две вершины связываются одним ребром, и для связи каждой последующей вершины с предыдущими требуется ребро, следовательно, для связи р вершин необходимо и достаточно р - 1 ребер.
При добавлении в дерево ребра образуется цикл, а при удалении хотя бы одного ребра дерево распадается на компоненты, каждая из которой представляет собой также дерево или изолированную вершину. Несвязный граф, компоненты которого являются деревьями, называется лесом (лес из к деревьев, содержащий р вершин, имеет в точности
р - к ребер). Сказанное иллюстрируется на примере дерева (рис. 11, а), которое превращается в циклический граф добавлением ребра (рис. 11, б) и распадается на лес из двух деревьев T1 и T2 при удалении ребра е (рис. 11, в).
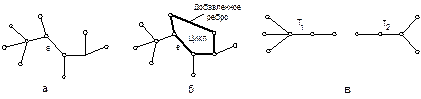
|
| Рис. 11. Дерево (а), образование цикла при введении дополнительного ребра (б) и лес, который образуется после удаления ребра е (в). |
Обычно деревья считаются существенно различными, если они не изоморфны. На рис. 12 показаны все возможные различные деревья с шестью вершинами. С увеличением числа вершин количество различных деревьев резко возрастает (например, при р = 20 их насчитывается около миллиона). Среди различных деревьев выделяются два важных частных случая: последовательное дерево, представляющее собой простую цепь, и звездное дерево, в котором одна из вершин (центр) смежна со всеми остальными вершинами.
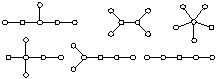
| 
|
| Рис. 12. Существенно различные деревья с шестью вершинами. | Рис. 13. Прадерево с
корнем  . .
|
Рассматриваются также деревья с ориентированными ребрами (дугами). Ориентированное дерево называется прадеревом с корнем  , если существует путь между вершиной
, если существует путь между вершиной  любой другой его вершиной (рис. 13). Ясно, что прадерево имеет единственный корень.
любой другой его вершиной (рис. 13). Ясно, что прадерево имеет единственный корень.
До сих пор рассматривались деревья как минимальные связные графы на множестве р вершин. Важное значение имеет и другая точка зрения, когда деревья или лес являются частями некоторого графа, т. е. образуются из его ребер. Любая связная совокупность ребер, не содержащая контуров, вместе с инцидентными им вершинами образует дерево графа (рис. 14, а). Если такое дерево является су графом (содержит все вершины графа), то оно называется покрывающим деревом или остовом (рис. 14, б). Так как петля представляет собой простейший цикл, состоящий из единственного ребра, то она не может входить в состав любого дерева графа.
Ребра графа, которые принадлежат его дереву, называют ветвями. Если дерево покрывает граф, то множество ребер графа разбивается на два подмножества: подмножество ветвей и подмножество ребер дополнения дерева, называемых хордами. При этом связный (р, q) - граф содержит v = р - 1 ветвей и 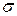 = q - р + 1 хорд. Если граф несвязный, то совокупность, остовов R его компонент образует покрывающий лес. В этом случае
= q - р + 1 хорд. Если граф несвязный, то совокупность, остовов R его компонент образует покрывающий лес. В этом случае 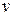 = р - R
= р - R
и 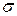 = q - р + R.
= q - р + R.
|
| Рис. 14. Дерево как часть графа (выделено жирными линиями): а — дерево; б — остов (покрывающее дерево). |
Деревья играют важную роль в различных прикладных задачах, когда, например, речь идет о связи каких-либо объектов минимальным числом каналов (линий связи, дорог, коммуникаций) с определенными свойствами. С помощью дерева определяется система координат при моделировании цепей и систем различной физической природы. Деревья используются в качестве моделей при рассмотрении иерархических систем объектов, структурных формул органических соединений и т. п.
13. Планарность. Граф называют плоским (планарным), если существует изоморфный ему граф (геометрическая реализация), который может быть изображен на плоскости без пересечения ребер. Например, хотя в одном из графов на рис. 6 ребра пересекаются, изоморфные ему не имеют пересечений, следовательно, он плоский.
На рис. 15 показаны два неплоских графа, играющие фундаментальную роль в теории планарности и называемые графами Понтрягина - Куратовского. Полный пятиугольник (рис. 15,а) представляет собой простой неплоский графе минимальным числом вершин (полный графе четырьмя вершинами - плоский, а удаление из пятиугольника хотя бы одного ребра также превращает его в плоский граф). Двудольный граф (рис. 15, б) является моделью известной задачи о трех домах и трех колодцах: можно ли проложить от домов к каждому колодцу дороги так, чтобы они не пересекались (враждующие соседи должны иметь возможность пользоваться всеми колодцами, но не хотят встречаться на дорогах).

|
| Рис. 15. Графы Понтрягина - Куратовского: а - полный пятиугольник; б — двудольный граф. |
Свойства планарности не нарушаются, если некоторое ребро разбить на два введением новой вершины второй степени или заменить два ребра, инцидентные вершине второй степени, одним ребром, удалив эту вершину. Два графа называют гомеоморфными (изоморфными с точностью до вершин второй степени), если после удаления из них вершин второй степени и объединения инцидентных этим вершинам ребер, они оказываются изоморфными (рис. 16). Очевидно, граф, гомеоморфный плоскому графу, также плоский.
Строго доказывается, что граф является плоским тогда и только тогда, когда он не содержит подграфа, гомеоморфного одному из графов Понтрягина - Куратовского.

| Рис. 16. Гомеоморфные графы. |
Планарность является существенным свойством графов, которые моделируют коммуникации и связи между объектами на плоскости (дороги между населенными пунктами, водопроводные и газопроводные сети, линии передач электроэнергии, межсоединения на печатных платах электронных устройств и кристаллах интегральных схем). Плоскими графами представляются различные карты, с которыми, в частности, связана известная проблема четырех красок: всегда ли можно раскрасить области, на которые плоский граф делит поверхность, так, чтобы никакие две смежные области не были окрашены в одинаковый цвет и чтобы при этом было использовано
не более четырех цветов? Доказано, что для такой раскраски в любом случае достаточно пяти красок, но никто еще не привел примера, когда пять красок действительно необходимы. Проблема остается нерешенной, несмотря на огромные усилия многих выдающихся математиков, которые штурмуют ее более столетия.
14. Графы и отношения. Пусть на множестве Х задано бинарное отношение А. Ему соответствует ориентированный граф, вершины которого отображают элементы из X, а дуга (хi, xj), где (хi, xj 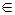 X), существует тогда и только тогда, когда(хiАxj). Обратно, множество ориентированных дуг графа (без строго параллельных дуг), заданных упорядоченными парами (хi, xj), можно рассматривать как бинарное отношение на множестве X.
X), существует тогда и только тогда, когда(хiАxj). Обратно, множество ориентированных дуг графа (без строго параллельных дуг), заданных упорядоченными парами (хi, xj), можно рассматривать как бинарное отношение на множестве X.
Если бинарное отношение хАy устанавливает связь между элементами х из множества Х и элементами у из множества Y (х 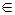 X, у
X, у 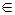 У), то граф такого отношения будет ориентированным биграфом.
У), то граф такого отношения будет ориентированным биграфом.
Следует заметить, что в общем случае орграф представляет нечто большее, чем бинарное отношение. Любое бинарное отношение, определенное на некотором множестве, можно представить соответствующим орграфом, вершины которого соответствуют элементам этого множества. Однако орграф с параллельными дугами позволяет отражать более общие связи между объектами, чем бинарные отношения.
ОСНОВЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
1. Чем занимается математическая логика? Логика как искусство рассуждении зародилась в глубокой древности. Начало науки о законах и формах мышления связывают с именем Аристотеля. Прошло два тысячелетия, прежде чем Лейбниц предложил ввести в логику математическую символику и использовать ее для общих логических построений. Эту идею последовательно реализовал в прошлом столетии Джордж Буль и тем самым заложил основы математической (символической) логики.
Главная цель применения в логике математической символики заключалась в том, чтобы свести операции с логическими заключениями к формальным действиям над символами. При этом исходные положения записываются формулами, которые преобразуются по определенным законам, а полученные результаты истолковываются в соответствующих понятиях.
Бурное развитие математической логики связано, прежде всего, с задачами обоснования математики, где она используется для доказательства непротиворечивости исходных понятий и правильности рассуждении и выводов математических теорий. Некоторые ученые даже склонны рассматривать логику как одну из наиболее общих наук, частью которой является сама математика.
В последние десятилетия логика находит все более широкое применение в технике при исследовании и разработке релейно-контактных схем, вычислительных машин, дискретных автоматов. Ее методы используются в теории преобразования и передачи информации, теории вероятностей и комбинаторном анализе. Математическая логика начинает внедряться в такие нематематические области, как экономика, биология, медицина, психология, языкознание, право. Интенсивно развиваются специальные разделы математической логики, призванные обслуживать конкретные области науки и техники.
Столь энергичный выход математической логики за пределы математики объясняется тем, что ее аппарат легко распространяется на объекты самой общей природы, лишь бы только они характеризовались конечным числом состояний.
Двузначная логика имеет дело с такими объектами, которые принимают одно из двух возможных значений (истинное или ложное высказывание, высокое или низкое напряжение, наличие или отсутствие заданного признака у объекта и т. п.). Объекты, которые могут принимать значения из конечного множества, содержащего больше двух элементов, называют многозначными. Они либо сводятся каким-нибудь способом к двузначным объектам, либо обслуживаются аппаратом многозначной логики.
Устоявшееся представление о математической логике как науке, изучающей законы мышления с применением аппарата математики, главным образом, для нужд самой математики, в современных условиях становится слишком узким. С расширением областей применения и дальнейшим развитием математической логики изменяется и взгляд на нее. Объектами математической логики являются любые дискретные конечные системы, а ее главная задача – структурное моделирование таких систем.
2. Булевы функции. Объекты с двумя возможными состояниями характеризуются булевыми переменными, которые способны принимать лишь два различных значения. Для обозначения этих двух значений обычно используются цифры 0 и 1 или буквы Л (ложно)
и И (истинно).
Отношения между булевыми переменными представляются булевыми функциями, которые подобно числовым функциям могут зависеть от одной, двух и, вообще, n переменных (аргументов). Запись у = f(x1, x2, …,xN) означает , что у - функция аргументов x1, x2, …,xN. Важнейшая особенность булевых функций состоит в том, что они, как и их аргументы, принимают свои значения из двухэлементного множества {0,1}, или (И, Л}, т. е. характеризуются одним из двух возможных состояний.
Функции небольшого числа переменных можно задавать с помощью таблиц, подобных таблицам сложения и умножения одноразрядных чисел. Для этого нужно только указать значения функции для каждой комбинации значений ее аргументов. Основными в двузначной логике являются следующие три функции.
Отрицание - функция у = f(х), принимающая значения 1, когда х = 0, и значение 0, когда х = 1; она обозначается у = 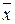 (читается «не х»).
(читается «не х»).
Дизъюнкция — функция у = f(x1, x2), принимающая значение 0 тогда и только тогда, когда оба аргумента имеют значение 0; она обозначается у = x1 \/ x2 (читается «у = x1 или x2»).
Конъюнкция—функция у = f(x1, x2), принимающая значение 1 тогда и только тогда, когда оба аргумента имеют значение 1; она обозначается у = x1 /\ x2 («у = x1 и x2»).
Таблицы для этих функций имеют вид:
|
|
| x1 \/ x2 | x1 /\ x2 | ||||||
| x1 | x2 |
| x1 | x2 | |||||
| x | 
| 0 | 1 | 0 | 1 | ||||
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | ||
3. Логические операции и формулы. Булевы функции можно рассматривать как логические операции над величинами, принимающими два значения - 0 и 1. Отрицание - это одноместная операция, а дизъюнкция и конъюнкция — двухместные операции. При этом выражения 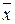 , x1 \/ x2, x1 /\ x2 являются логическими формулами.
, x1 \/ x2, x1 /\ x2 являются логическими формулами.
Более сложные формулы получаются замещением входящих в них переменных другими логическими формулами, которые обычно заключаются в скобки. Например, положив x1 =  и x2 = b /\ c из x1 V x2,имеем (
и x2 = b /\ c из x1 V x2,имеем (  ) \/ (b
) \/ (b 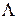 c). Каждая формула определяет некоторую булеву функцию. Ее значение при различных значениях переменных определяется на основании таблиц функций, приведенных в (2). Так, при а = 0, b = 1 и с = 0 имеем:
c). Каждая формула определяет некоторую булеву функцию. Ее значение при различных значениях переменных определяется на основании таблиц функций, приведенных в (2). Так, при а = 0, b = 1 и с = 0 имеем:
x1 =  =
=  =1, x2 = b /\ с = 1 /\ 0 = 0 и x1 \/ x2 =
=1, x2 = b /\ с = 1 /\ 0 = 0 и x1 \/ x2 =  \/ (b \/ c) = 1 \/ 0 = 1. Аналогично получаем значения функции и при других комбинациях значений аргументов.
\/ (b \/ c) = 1 \/ 0 = 1. Аналогично получаем значения функции и при других комбинациях значений аргументов.
Две функции (как и определяющие их формулы) считаются равносильными,если при любых значениях аргументов эти функции (формулы) принимают одинаковые значения. Равносильные функции соединяются знаком равенства, например: (х /\ у) \/ 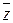 = (
= ( 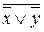 ) /\ z или ((х \/
) /\ z или ((х \/ 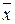 ) /\ у) \/ (у \/ х) == х \/ у. Равносильность функций проверяется по таблицам основных операций, причем необходимо сравнить их значения для всех комбинаций значений переменных.
) /\ у) \/ (у \/ х) == х \/ у. Равносильность функций проверяется по таблицам основных операций, причем необходимо сравнить их значения для всех комбинаций значений переменных.
4. Булева алгебра. Множество всех булевых функций вместе с операциями отрицания, конъюнкции и дизъюнкции образует булеву алгебру.
На основе определения основных операций нетрудно убедиться в справедливости следующих тождеств (свойств) булевой алгебры:
коммутативность
х \/ y = y \/ х, х /\ y = y /\ х;
ассоциативность
х \/ ( y \/ z) = (х \/ y) \/ z, х /\ ( y /\ z) = (х /\ y) /\ z;
дистрибутивность
х /\ ( y \/ z) = (х /\ y) /\ (х \/ z), х \/ ( y /\ z) = (х /\ y) /\ (х \/ z);
свойство констант
х \/ 0 = x, х /\ 1 = x;
свойство отрицания
х \/  = 1, х /\
= 1, х /\  = 0.
= 0.
5. Тождественные преобразования. Приведенные свойства позволяют получить ряд других важных законов и тождеств уже без обращения к таблицам соответствия: 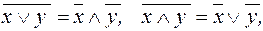 (законы де Моргана), х \/ (х /\ у) = х /\ (х \/ у) = х (законы поглощения) х \/ х = х /\ х = х (законы идемпотентности), а также тождества
(законы де Моргана), х \/ (х /\ у) = х /\ (х \/ у) = х (законы поглощения) х \/ х = х /\ х = х (законы идемпотентности), а также тождества 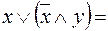 x \/ y; (x /\ y) \/ (x /\ z) \/ (x /\
x \/ y; (x /\ y) \/ (x /\ z) \/ (x /\ 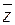 ); = (x /\ z) \/ (y /\
); = (x /\ z) \/ (y /\ 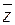 );
);  = x;
= x;  = 0;
= 0;
 = 1; x \/ 1 =1; x /\ 0 = 0 и т. д.
= 1; x \/ 1 =1; x /\ 0 = 0 и т. д.
Так, законы идемпотентности доказываются следующими преобразованиями:
х \/ х = (х \/ х) /\ 1 = (х \/ х) /\ (х \/  ) = х \/ (х /\ (х \/ х)) = х \/ 0 = х;
) = х \/ (х /\ (х \/ х)) = х \/ 0 = х;
х /\ х = (х /\ х) \/ 0 = (х /\ х) \/ (х /\  ) = х /\ (х \/
) = х /\ (х \/  ) = х /\ 1 = х.
) = х /\ 1 = х.
Используя полученные соотношения, имеем:
х \/ 1 = x \/ ( x \/  ) = (х \/ х) \/
) = (х \/ х) \/  = х \/
= х \/  = 1; x /\ 0 = x /\ ( x /\
= 1; x /\ 0 = x /\ ( x /\  ) = x /\
) = x /\  = 0.
= 0.
Доказательство законов поглощения имеет вид:
x \/ (x /\ y) = (x /\ 1) \/ (x /\ y) = x /\ (1 /\ y) = x /\ 1 = x;
x /\ (x \/ y) = (x \/ 0) /\ (x \/ y) = x \/ (y /\ 0) = x \/ 0 = x.
Соотношение 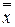 = х доказывается следующим образом:
= х доказывается следующим образом:
из х \/  = 1 по закону коммутативности следует
= 1 по закону коммутативности следует  \/ x = 1, откуда сравнением с
\/ x = 1, откуда сравнением с 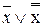 = 1 имеем х =
= 1 имеем х = 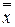 .
.
Интересно доказательство закона де Моргана. На основании свойств отрицания равенство функций  и
и 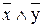 должно означать, что
должно означать, что
(х \/ у) \/ ( 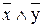 ) = 1 и (х \/ у) \/ (
) = 1 и (х \/ у) \/ ( 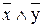 ) = 0.
) = 0.
Действительно,
(х \/ у) \/ ( 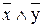 ) = ((х \/ у) \/
) = ((х \/ у) \/  ) /\ ((х \/ у) \/
) /\ ((х \/ у) \/  ) = (( x /\
) = (( x /\  ) \/ y ) /\ (x \/ (y \/
) \/ y ) /\ (x \/ (y \/  )) =
)) =
= (1 \/ y) /\ (x \/ 1) = 1 /\ 1 = 1, а также
(х \/ у) /\ ( 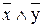 ) = (х /\ \/ (
) = (х /\ \/ ( 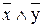 ) = (у /\ (
) = (у /\ ( 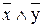 ) = ((x /\
) = ((x /\  ) /\
) /\  ) \/ ((y /\
) \/ ((y /\  ) /\
) /\  ) =
) =
= (0 /\  ) \/ (
) \/ (  /\ 0) = 0 \/ 0 = 0.
/\ 0) = 0 \/ 0 = 0.
Следовательно, соотношение  =
= 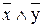 доказано. Аналогично доказывается и второй закон.
доказано. Аналогично доказывается и второй закон.
6. Упрощение записи формул. Операции дизъюнкции и конъюнкции удовлетворяют законам коммутативности и ассоциативности. Поэтому если переменные или формулы связаны только посредством одной из этих операций, то их можно выполнять в лгсбом порядке, а формулы записывать без скобок. Например:
((х1 \/ x2) \/ (х3 \/ x4) \/ х5 = х1 \/ x2 \/ х3 \/ x4 \/ х5,
а также (х1 /\ x2) /\ (x3 /\ (х4 /\ x5) = х1 /\ x2 /\ x3 /\ х4 /\ x5.
Если считать, что операция конъюнкции должна предшествовать операции дизъюнкции (конъюнкция связывает сильнее дизъюнкции), то можно опустить скобки, в которые заключены формулы со знаком конъюнкции. При наличии скобок в первую очередь должны выполняться операции внутри скобок, независимо от их старшинства. Обычно опускают также скобки, в которые заключены формулы со знаком отрицания.
Еще одно упрощение связано с символикой. Знак конъюнкции в формулах можно опустить и вместо х /\ у писать ху. Операцию конъюнкции часто называют логическим умножением, а операцию дизъюнкции - логическим сложением.
С учетом приведенных условий запись существенно упрощается. Например, формуле (x /\ (y /\ 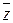 )) \/ ((
)) \/ ((  ) /\ z) соответствует запись
) /\ z) соответствует запись 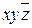 \/
\/  z.
z.
7. Переключательные схемы. В качестве одной из интерпретаций булевых функций рассмотрим электрическую схему, состоящую из источника напряжения (батареи), лампочки и одного или двух ключей (х1 и x2). Ключи управляются кнопками с двумя состояниями: кнопка нажата (1) и кнопка отпущена (0). Если в исходном состоянии ключ разомкнут, то при нажатии кнопки он замыкается.
Ключ может быть сконструирован и так, что в исходном состоянии он замкнут, тогда нажатие кнопки означает его размыкание, т. е. приводит к противоположному результату. Поэтому нормально замкнутые ключи обозначим через  .
.
При соответствующих состояниях кнопок лампочка принимает одно из двух состояний: горит (1) и не горит (0). Состояния кнопок отождествляются со значениями булевых переменных х1 и x2, а состояние лампочки — со значением функций этих переменных.
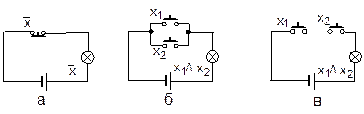
| Рис. 17. Переключательные схемы, соответствующие операциям отрицания (а), дизъюнкции (б) и конъюнкции (в) |
Операции отрицания соответствует схема с одним нормально замкнутым ключом (рис. 17, а). Если кнопка нажата (х = 1), ключ разомкнут и лампочка не горит, т. е. f(х) = 0; при отпущенной кнопке (х = 0) ключ замкнут и лампочка горит, т. е. f(x) = 1. Операциям дизъюнкции и конъюнкции соответствуют схемы с двумя нормально разомкнутыми ключами (рис. 17, б, в). Легко убедиться, что в схеме рис. 17, б лампочка горит при нажатии хотя бы одной из кнопок, а в схеме рис. 17, в - только при нажатии обеих кнопок одновременно.
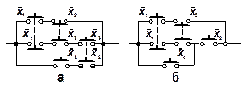
| Рис. 18. Переключательная схема, реализующая логическую функцию (а), и упрощенная схема(б). |
Любую сложную булеву функцию можно представить некоторой переключательной схемой. На рис. 18,а показана схема, реализующая функцию у = х1  \/
\/ 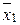 x2x3 \/ x3x4. Та же функция представляется равносильной формулой у = х1
x2x3 \/ x3x4. Та же функция представляется равносильной формулой у = х1  \/ (
\/ ( 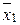 x2 \/ x4)x3, которой соответствует другая более простая схема (рис. 18, б). Следует иметь в виду, что ключи, обозначенные одинаковыми буквами (х или
x2 \/ x4)x3, которой соответствует другая более простая схема (рис. 18, б). Следует иметь в виду, что ключи, обозначенные одинаковыми буквами (х или 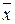 ), связаны между собой и управляются общей кнопкой.
), связаны между собой и управляются общей кнопкой.
В реальных устройствах используются ключи различной конструкции и физической природы (механические, электромагнитные, электронные, гидравлические, пневматические и т. д.) Однако при реализации логических функций многие технические особенности не имеют значения. Существенными свойствами контактных схем являются исходные положения ключей (нормально разомкнуты или нормально замкнуты) и способ их соединения между собой и внешними устройствами. Эта информация полностью отображается графом, ребра которого соответствуют ключам, а вершины - точкам их соединения. Ребра нормально разомкнутых ключей обозначаются соответствующей переменной (х), а нормально замкнутых - отрицанием переменной (х). Например, контактная схема (рис. 23, б) изображается графом, как показано на рис. 19, а.
При изображении контактных схем графами принимаются некоторые специфические условия и упрощения. Обычно переменные обозначаются в разрывах линий, изображающих ребра.
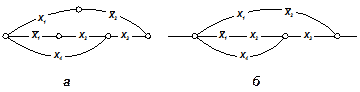
| Рис. 19. Граф переключательной схемы (а) и его упрощенное изображение (б). |
При этом ребрами считаются только такие линии, которые обозначены какой-либо переменной или ее отрицанием. Другие линии, не являющиеся ребрами графа, могут изображать входы и выходы схемы, связи с другими схемами и т. п. Кроме того, вершины второй степени могут не изображаться, так как им инцидентны пары последовательно соединенных ребер, из которых каждое обозначено соответствующей переменной.
На рис. 19,б показана контактная схема в обычно принятом виде.
8. Высказывания. Пусть х1 и x2 - некоторые высказывания, которые могут быть истинными (1) или ложными (0), например: «Я пойду в театр» (х1) и «Я встречу друга» (x2). Дизъюнкцией х1 \/ x2 является сложное высказывание «Я пойду в театр или встречу друга», а конъюнкцией х1 /\ x2 - высказывание «Я пойду в театр и встречу друга».
Ясно, что если высказывание истинно, то его отрицание ложно. Сложное высказывание, образованное дизъюнкцией двух высказываний, истинно при условии, что истинно хотя бы одно из них. Сложное высказывание, образованное конъюнкцией двух истинных высказываний истинно, если истинны оба эти высказывания одновременно.
Итак, высказывания можно рассматривать как двоичные переменные, а связки «не», «или», «и», с помощью которых образуются сложные высказывания, - как операции над этими переменными. В алгебре высказываний используются еще две операции: импликация х1 → x2, соответствующая связке «если, то» и эквиваленция х1 ~ x2, соответствующая связке «если и только если». Они задаются следующими таблицами:
| x1 ® x2 | x1 ~ x2 | |||||
| x1 | x2 |
| x1 | x2 | ||
| 0 | 1 | 0 | 1 | |||
| 0 | 1 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 1 | |
В нашем примере импликацией будет высказывание: «Если пойду в театр, то встречу друга», а эквиваленцией – пойду в театр, если и только если встречу друга». Как видно из таблиц, импликация высказываний ложна только в случае, когда первое из простых высказываний истинно, а второе ложно. Эквиваленция является истинным высказыванием, если оба простые высказывания истинны или ложны одновременно.
Обозначив буквами простые высказывания, можно представить сложное высказывание формулой с помощью соответствующих связок. Например, высказыванию «Если давление масла на шарик клапана больше усилия его пружины (х1), то масло открывает клапан (х2) и частично перетекает из нагнетательной полости во впускную (х3)» соответствует формула х1 → х2 х3.
9. Предикаты. Обычно высказывания выражают свойства одного или нескольких объектов. Содержательная часть высказывания играет роль определяющего свойства совокупности объектов, для которых это высказывание истинно, и называется предикатом. Например, высказывание «Иванов - отличник» истинно или ложно в зависимости от оценок, которые имеет данный студент. В то же время предикат «х - отличник» определяет подмножество отличников на некотором множестве студентов (группа, курс, факультет). Подставив вместо х фамилии студентов, получим множество высказываний. Совокупность истинных высказываний и будет соответствовать подмножеству отличников.
Предикат представляет собой логическую функцию Р(х), принимающую, как и булевы функции, значение 0 или 1, но в отличие от них, значения аргумента х выбираются из некоторого множества М объектов (х  М). В общем случае такая функция может зависеть от многих аргументов х1, х2, . . .,хn, принимающих значения из одного и того же или различных множеств. Ее записывают Р(х1, х2, . . .,хn) и называют n-местным предикатом. Например: «х - четное число», «х - компонент цепи» - одноместные предикаты Р(х);
М). В общем случае такая функция может зависеть от многих аргументов х1, х2, . . .,хn, принимающих значения из одного и того же или различных множеств. Ее записывают Р(х1, х2, . . .,хn) и называют n-местным предикатом. Например: «х - четное число», «х - компонент цепи» - одноместные предикаты Р(х);
«х брат у», «х меньше у» — двуместные предикаты Р(х, у); «х и у - родители z»,
«х - сумма y и z» - трехместные предикаты Р(х, y, z) и т. д. Если аргументы х1, х2, ... ,хn замещены конкретными значениями (объектами), то предикат переходит в высказывание, которое рассматривают как 0 - местный предикат.
Так как предикаты способны принимать только значения 0 и 1, то их, как и булевы переменные, можно связывать логическими операциями. В результате получаем формулы, определяющие более сложные предикаты. Так, если Р(х) означает «х - инженер», а Q(х) - «x - сотрудник нашего отдела», то Р(х) /\ Q(х) = R(х) есть одноместный предикат «х - инженер и сотрудник нашего отдела» или проще «х - инженер нашего отдела». Очевидно, если Р - множество инженеров, а 0 - множество сотрудников данного отдела, то этот предикат соответствует пересечению Р  Q. Таким образом, имеет место тесная связь между логикой предикатов и операциями над множествами.
Q. Таким образом, имеет место тесная связь между логикой предикатов и операциями над множествами.
10. Однородные функции. Если аргументы принимают значения из того же множества, что и сама функция, то ее называют однородной функцией. В этом случае X 1 = Х2 = ... = Х n = N и однородная функция, рассматриваемая как закон композиции  определяет некоторую п-местную операцию на конечном множестве N.
определяет некоторую п-местную операцию на конечном множестве N.
Областью определения однородной функции у = f (х1, х2, ..., xn ) служит множество наборов (х1, х2, ..., xn), называемых словами, где каждый из аргументов х1, х2, ..., xn замещается буквами k -ичного алфавита {0, 1, ..., k -1}. Количество п букв в данном слове определяет его длину.
Очевидно, число всевозможных слов длины n в k-ичном алфавите равно kn. Так как каждому такому слову имеется возможность предписать одно из k значений множества N, то общее количество однородных функций от п переменных выражается числом k ( kn ).
Если буквами алфавита служат числа от 0 до k - 1, то каждое слово (х1, х2, ..., xn) символически представляется упорядоченной последовательностью п таких чисел и рассматривается как запись n-разрядного числа в позиционной системе счисления с основанием k , т. е. x 1 kn -1 + x 2 kn –2 + … + xn -1 k 1 + xnk 0 . Числа q = = 0, 1, ..., kn - 1 служат номерами слов и тем самым на множестве всех слов вводится естественная упорядоченность (отношение строгого порядка). Аналогично номерами функций можно считать kn -разрядные числа в той же системе счисления.
Различные слова длины п в данном алфавите образуются как n-перестановки с повторениями (2. 10. 1). Так, в трехзначном алфавите {0, 1, 2} словами длины 4 будут все четырехразрядные числа с основанием k = 3, т. е. 0000, 0001, 0002, 0010, 0011, ..., 2221, 2222, которые соответствуют десятичным числам от 0 до 80 = 2 • З3+ 2 • З2+ 2 • З1 + 2 • 30. Поставив каждому такому четырехразрядному числу в соответствие одну из букв алфавита {0, 1, 2}, получим некоторую функцию четырех переменных fi (х1, х2, x 3, x 4 ), причем количество таких функций выражается огромным числом 381.
Пусть алфавит состоит из трех букв русского алфавита {о, п, т}. Множество пятибуквенных слов в этом алфавите состоит из 35 = 243 элементов. Наряду с такими имеющими прямой смысл словами, как «топот» и «потоп», оно также включает все другие 5-перестановки, например: «ооппт», «поппп», «тттоп» и др.
Примерами однородных логических функций двух переменных могут служить операции сложения и умножения одноразрядных m-значных чисел по модулю т (2. 8. 7), внутренние операции поля Галуа (2. 8. 9) с четырехзначным алфавитом {0, 1, А, В} и т. п.
11. Табличное задание функций. Как и бинарный закон композиции (2. 7. 2), однородная функция двух переменных может быть задана таблицей соответствия (матрицей), строки и столбцы которой соответствуют буквам алфавита. Таким способом представлялись функции одной и двух переменных в (1. 5. 2),(1. 5. 8) и (1. 5. 10). Для представления функций трех и большего числа переменных потребовались бы трехмерные и, вообще, n-мерные таблицы. Этого можно избежать, если столбцы матрицы поставить в соответствие не буквам алфавита, а словам, т. е. образовать kn столбцов. Для каждой функции отводится строка, клетки которой заполняются буквами из данного алфавита. Матрица всех функций п переменных в k-значном алфавите содержит  строк и называется общей таблицей соответствия. Например, для k = 3 и п = 2 такая матрица имеет вид:
строк и называется общей таблицей соответствия. Например, для k = 3 и п = 2 такая матрица имеет вид:
| x1 x2 | 0 0 | 0 1 | 0 2 | 1 0 | 1 1 | 1 2 | 2 0 | 2 1 | 2 2 |
| y0 y1 y2 … y2361 … y19682 | 0 0 0 . 0 . 2 | 0 0 0 . 1 . 2 | 0 0 0 . 0 . 2 | 0 0 0 . 0 . 2 | 0 0 0 . 1 . 2 | 0 0 0 . 2 . 2 | 0 0 0 . 2 . 2 | 0 0 0 . 0 . 2 | 0 1 2 . 1 . 2 |
Номера столбцов определяются расположенными над ними n-разрядными числами с основанием k , каждое из которых читается сверху вниз. Номера функций отождествляются с kn-разрядными числами, которые соответствуют строкам матрицы в той же системе счисления.
12. Двузначные однородные функции. Наиболее простым и в то же время важнейшим классом однородных функций являются двузначные (булевы) функции, частично рассмотренные в (1.5. 2) и последующих пунктах.
Областью определения булевых функций от п переменных служит множество слов длины п. Они представляют собой всевозможные наборы из п двоичных цифр и их общее количество равно 2n.
Число всевозможных булевых функций п переменных v = 2n быстро возрастает с увеличением п (при п = 3 оно равно 256, а при п = 5 превышает 4 миллиарда). Но функции одной и двух переменных еще можно перечислить и подробно исследовать, так как их количество сравнительно невелико (v = 4 при п = 1 и v = 16 при п = 2).
13. Булевы функции одной переменной. Общая таблица соответствия для булевых функций одной переменной имеет вид (справа указаны обозначения функций):
| x | 0 | 1 | y |
| y0 | 0 | 0 | 0 |
| y1 | 0 | 1 | x |
| y2 | 1 | 0 | 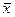
|
| y3 | 1 | 1 | 1 |
Две функции у0 = 0 и у3 = 1 представляют собой функции-константы (тождественный нуль и тождественная единица), таккакони не изменяют своих значений при изменении аргумента. Функция y 1 = х повторяет значения переменной х и потому просто совпадает с ней.
Единственной нетривиальной функцией является у2 = 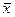 , называемая отрицанием или инверсией (
, называемая отрицанием или инверсией ( 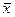 читается «не х»). Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
читается «не х»). Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
14. Булевы функции двух переменных. Все 16 функций двух переменных приведены в табл. 6, где указаны условные обозначения, названия и чтения функций (в скобках даны встречающиеся в литературе варианты).
Шесть из приведенных функций не зависят от x 1 или x 2 (или от обоих вместе). Это две константы (у0 = 0 и у15 = 1), повторения (у3 = х1 и у5 = х2) и отрицания (у10 = 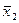 и у12 =
и у12 =  ), являющиеся функциями одной переменной (х1 или x2). Из остальных десяти функций две (y 4 и y 11) отличаются от соответствующих им (y 2 и y 13) лишь порядком расположения аргументов и поэтому не являются самостоятельными. Поэтому из 16 булевых функций двух переменных только восемь являются оригинальными (у1, у2, у6, у7, у8, у9, у13, у14).
), являющиеся функциями одной переменной (х1 или x2). Из остальных десяти функций две (y 4 и y 11) отличаются от соответствующих им (y 2 и y 13) лишь порядком расположения аргументов и поэтому не являются самостоятельными. Поэтому из 16 булевых функций двух переменных только восемь являются оригинальными (у1, у2, у6, у7, у8, у9, у13, у14).
Рассмотрение булевых функций одной, двух и большего числа переменных показывает, что всякая функция от меньшего числа переменных содержится среди функций большего числа переменных. Функции, которые сводятся к зависимости от меньшего числа переменных, называют вырожденными, а функции, существенно
Таблица 6
Булевые функции двух переменных
| x1 x2 | 0 0 1 1 0 1 0 1 | Обозначения | Названия | Чтение |
| y0 | 0 0 0 0 | 0 | Константа 0 (тождественный нуль, всегда ложно) | Любое 0 |
| y1 | 0 0 0 1 | x1x2; 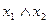 (
(  ; ;  ) )
| Конъюнкция (совпадение, произведение, пересечение, логическое «и») | x1 и x2 (и x1 и x2) |
| y2 | 0 0 1 0 | 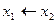 (
(  ; ; 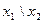 ) )
| Отрицание импликации (совпадение с запретом, антисовпадение, запрет) | x1, но не x2 |
| y3 | 0 0 1 1 | x1 | Повторение (утверждение, доминация) первого аргумента | Как x1 |
| y4 | 0 1 0 0 | 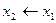 (
(  ; ; 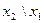 ) )
| Отрицание обратной импликации (обратное антисовпадение) | Не x1, но x2 |
| y5 | 0 1 0 1 | x2 | Повторение (утверждение, доминация) второго аргумента | Как x2 |
| y6 | 0 1 1 0 | x1 + x2
( 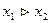 ; ; 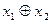 ) )
| Сумма по модулю 2 (неравнозначность, антиэквивалентность) | x 1 не как x 2 (или x 2 или x 1) |
| y7 | 0 1 1 1 | 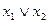 (x1 + x2;
(x1 + x2; 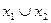 ) )
| Дизъюнкция (разделение, логическая сумма, сборка, логическое «или») | x 1 или x 2 (x 1 или хотя бы x 2) |
| y8 | 1 0 0 0 |  (
( 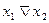 ; ;  ) )
| Стрелка Пирса (функция Вебба, отрицание дизъюнкции, логическое «не – или») | Ни x1,ни x2 |
| y9 | 1 0 0 1 | x1 ~ x2
( 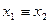 ; ;  ) )
| Эквиваленция (равнозначность, эквивалентность, взаимозависимость) | x 1 как x 2 (x 1, если и только если x 2) |
| y10 | 1 0 1 0 | 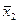 (x2; ~x2;
(x2; ~x2;  x2) x2)
| Отрицание (инверсия) второго аргумента (дополнение к первой переменной) | Не x2 |
| y11 | 1 0 1 1 | 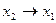 (
( 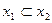 ; ; 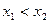 ) )
| Обратная импликация (обратное разделение с запретом, обратная селекция) | Если x 2, то x 1 (x 1 или не x 2) |
| y12 | 1 1 0 0 |  (x1; ~x1;
(x1; ~x1;  x1) x1)
| Отрицание (инверсия) первого аргумента (дополнение к первой переменной) | Не x1 |
| y13 | 1 1 0 1 | 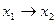 (
(  ; ;  ) )
| Импликация (разделение с запретом, следование, селекция) | Если x 1, то x 1 (не x 1 или x 2) |
| y14 | 1 1 1 0 | x1 / x2
(  ; ; 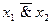 ) )
| Штрих Шеффера (отрицание конъюнкции, несовместность, логическое «не – и») | Не x1 или не x2 |
| y15 | 1 1 1 1 | 1 | Константа 1 (тождественная единица, всегда истино) | Любое 1 |
зависящиеот всех переменных, являются невырожденными. Так, среди функций одной переменной имеются две вырожденные (константы 0 и 1, которые можно рассматривать как функции от нуля переменных), функции двух переменных содержат те же константы и четыре функции одной переменной и т. д.
15. Зависимость между булевыми функциями. Из табл. 6 видно, что между функциями имеются зависимости 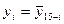 (i = 0, 1, ... ..., 15), на основании которых можно записать соотношения для констант
(i = 0, 1, ... ..., 15), на основании которых можно записать соотношения для констант  и
и  , для функции одной переменной х =
, для функции одной переменной х = 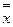 и для функций двух переменных:
и для функций двух переменных:
x 1 x 2 = 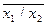 ;
; 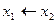 =
=  ; x 1 + x 2 =
; x 1 + x 2 = 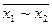 ;
; 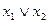 =
=  ,
,
или
x 1/x 2 =  ;
; 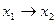 =
=  ; x 1 ~ x 2 =
; x 1 ~ x 2 =  ;
;  =
=  .
.
Из этих зависимостей следует, что любая функция двух переменных (включая константы) выражается в аналитической форме через совокупность шести функций, содержащей отрицание 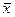 и любую из каждой пары функций {y 0, y 15},{y 1, y 14},{y 2, y 13}, {y 6, y 9}, {y 7, y 8}. Например, такой совокупностью могут служить функции: константа 0, отрицание`х, конъюнкция х1 x 2, дизъюнкция
и любую из каждой пары функций {y 0, y 15},{y 1, y 14},{y 2, y 13}, {y 6, y 9}, {y 7, y 8}. Например, такой совокупностью могут служить функции: константа 0, отрицание`х, конъюнкция х1 x 2, дизъюнкция 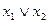 ,эквиваленция х1 ~ x 2 и импликация
,эквиваленция х1 ~ x 2 и импликация 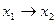 . Как уже упоминалось в (1. 5. 8), они используются в исчислении высказываний.
. Как уже упоминалось в (1. 5. 8), они используются в исчислении высказываний.
Выбранная таким способом совокупность шести функций является избыточной. Можно показать, что импликация и эквиваленция выражаются через остальные функции этой совокупности:
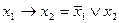 ;
;
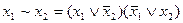 .
.
Для этого достаточно построить таблицу соответствия и сравнить ее с табл. 6:
| x1 x2 | 0 0 | 0 1 | 1 0 | 1 1 | |

| 1 | 1 | 0 | 0 | |
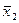
| 1 | 0 | 1 | 0 | |
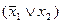
| 1 | 1 | 0 | 1 | 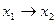
|

| 1 | 0 | 1 | 1 | |
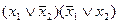
| 1 | 0 | 0 | 1 | 
|
Таким образом, комплект элементарных функций сокращается до четырех: константа 0, отрицание 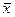 , конъюнкция x 1 x 2 и дизъюнкция
, конъюнкция x 1 x 2 и дизъюнкция 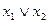 . Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Так, из законов де Моргана и свойства двойного отрицания вытекают тождества:
. Этот комплект обладает существенными удобствами и часто применяется на практике, но и он может быть сокращен. Так, из законов де Моргана и свойства двойного отрицания вытекают тождества:
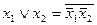 ; x 1 x 2 =
; x 1 x 2 = 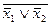 .
.
Отсюда следует, что булевы функции выражаются через отрицание и конъюнкцию или через отрицание и дизъюнкцию.
Более того, для записи любой булевой функции достаточно только одной из двух элементарных функций — стрелки Пирса или штриха Шеффера. Это вытекает из соотношений (их доказательство приводится аналогично с помощью таблиц соответствия):
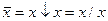 ;
;
x 1 x 2 = (x 1/x 2)/(x 1/x 2);  .
.
16. Булевы функции многих переменных. С помощью суперпозиции функций, т. е. подстановки в логические формулы вместо переменных некоторых булевых функций, можно получить более сложные функции от любого числа переменных. Например, подставляя в выражение а b формулы  и
и  , а также
, а также 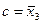 , получаем
, получаем  . Таблица соответствия для сложных формул записывается на основании общей таблицы для элементарных функций. Для данного примера она имеет вид:
. Таблица соответствия для сложных формул записывается на основании общей таблицы для элементарных функций. Для данного примера она имеет вид:
| x1 x2 x3 | 0 0 0 | 0 0 1 | 0 1 0 | 0 1 1 | 1 0 0 | 1 0 1 | 1 1 0 | 1 1 1 |
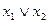
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
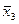
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |

| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |

| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
Если на всех наборах значений переменных функция принимает значение 0 или 1, то она вырождается в соответствующую константу и называется тождественным нулем или тождественной единицей.
Например, 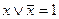 ;
; 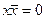 ;
; 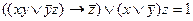 ;
; 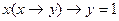 и т. п.
и т. п.
17. Геометрическое представление. Область определения булевых функций от п переменных у = f(х1, x2, ...,xn) можно рассматривать как совокупность n-мерных векторов (слов длины n), компонентами которых являются буквы 0 и 1 двоичного алфавита. При п = 3 каждый вектор представляется вершиной единичного куба в трехмерном пространстве (рис. 20). В общем случае совокупность векторов (х1, x2, ...,xn) отображается на множество вершин n-мерного куба.Всетакие вершины образуют логическое пространство.


Булева функция отображается на n-мерном кубе путем выделения вершин, соответствующих векторам (х1, x2, ...,xn) на которых булева функция у = f(х1, x2, ...,xn) принимает значения 1. Обычно такие вершины отмечают жирными точками. Так, на рис. 20 отображена функция  в соответствии с таблицей из (8).
в соответствии с таблицей из (8).
2. Нормальные формы. Дизъюнктивная (конъюнктивная) нормальная форма — это дизъюнкция (конъюнкция) конечного числа различных членов, каждый из которых представляет собой конъюнкцию (дизъюнкцию) отдельных переменных или их отрицаний, входящих в данный член не более одного раза.
Данная формула приводится к нормальной форме следующими путем: 1) с помощью законов де Моргана формула преобразуется! к такому виду, чтобы знаки отрицания относились только к отдельным переменным; 2) на основе первого (второго) дистрибутивного закона формула сводится к дизъюнкции конъюнкций (конъюнкции дизъюнкций); 3) полученное выражение упрощается в соответствии с тождествамихх = хи 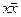 =0
=0  и
и 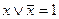 ).
).
Пример: 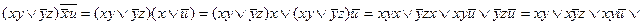
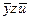 (дизъюнктивная нормальная форма);
(дизъюнктивная нормальная форма); 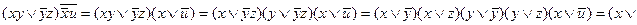
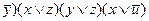 (конъюнктивная нормальная форма).
(конъюнктивная нормальная форма).
Члены дизъюнктивной (конъюнктивной) нормальной формы, представляющие собой элементарные конъюнкции (дизъюнкции) k букв, называют минитермами (макстермами) k-го ранга. Так, в приведенных выше формах ху - минитерм второго ранга,  - минитерм третьего ранга, а
- минитерм третьего ранга, а 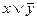 - макстерм второго ранга.
- макстерм второго ранга.
Если исходная формула содержит другие операции, то они предварительно выражаются через дизъюнкцию, конъюнкцию и отрицание, например:

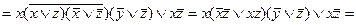
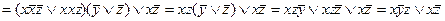
3. Совершенные нормальные формы. Если в каждом члене нормальной формы представлены все переменные (либо в прямом, либо в инверсном виде), то она называется совершенной нормальной формой.
Можно показать, что любая булева функция, не являющаяся тождественным нулем (единицей), имеет одну и только одну совершенную дизъюнктивную (конъюнктивную) нормальную форму. Если какой-либо член  дизъюнктивной (конъюнктивной) нормальной формы не содержит переменной xi то она вводится тождественным преобразованием
дизъюнктивной (конъюнктивной) нормальной формы не содержит переменной xi то она вводится тождественным преобразованием 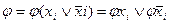 (соответственно
(соответственно 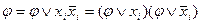 ). В силу тождеств
). В силу тождеств  и
и 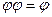 одинаковые члены, если они появляются, заменяются одним таким членом.
одинаковые члены, если они появляются, заменяются одним таким членом.
Продолжая второй пример из (2), приведем данную функцию к совершенной дизъюнктивной нормальной форме: 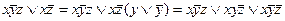 . Приведение к совершенной конъюнктивной нормальной форме иллюстрируется следующим примером:
. Приведение к совершенной конъюнктивной нормальной форме иллюстрируется следующим примером:


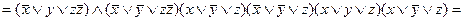

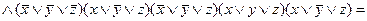

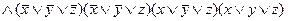
4. Проблема разрешимости. Формула (или соответствующая ей функция) называется выполнимой, если она не является тождественным нулем или единицей. Решение с помощью конечного числа действий вопроса, является ли данная формула выполнимой, т. е. не равна ли она тождественно нулю или единице, носит название проблемы разрешимости.
Ответ на этот вопрос можно получить, построив для данной формулы таблицу соответствия, что сводится по существу к определению значений формулы при всевозможных наборах значений входящих в нее переменных. Если на всех наборах формула принимает значения только 0 или только 1, то она невыполнима.
При большом количестве переменных такой способ практически неосуществим из-за огромного числа возможных наборов значений переменных. Более удобный путь - приведение формулы к нормальной форме. Если в процессе такого приведения формула не обращается в тождественный 0 или 1, то это свидетельствует о ее выполнимости.
5. Конституенты и представление функций. Для совокупности переменных х1, х2, ..., х n выражение 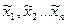 называют конституентой единицы, а выражение
называют конституентой единицы, а выражение 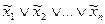 - конституентой нуля (
- конституентой нуля ( 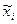 означает либо xi , либо
означает либо xi , либо  ). Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания - нулю (единице). Например, конституенте единицы
). Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания - нулю (единице). Например, конституенте единицы  соответствует набор (1011), а конституенте нуля
соответствует набор (1011), а конституенте нуля  - набор (1001).
- набор (1001).
Так как совершенная дизъюнктивная (конъюнктивная) нормальная форма является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею булева функция f(х1, х2, ..., х n) обращается в единицу (нуль) только при наборах значений переменных х1, х2, ..., х n , соответствующих этим конституентам. На остальных наборах эта функция обращается в нуль (единицу).
Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей. Для этого необходимо записать дизъюнкции (конъюнкции) конституент единицы (нуля), соответствующих наборам значений переменных, на которых функция принимает значение, равное единице (нулю). Например функции, заданной таблицей
| x1 x2 x3 | 0 0 0 | 0 0 1 | 0 1 0 | 0 1 1 | 1 0 0 | 1 0 1 | 1 1 0 | 1 1 1 |
| Y | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
соответствуют совершенные нормальные формы:

 .
.
Полученные выражения можно преобразовать к другому виду на основании свойств булевой алгебры.
4. Упрощение формул. Между формулой, выражающей булеву функцию, и функциональной схемой, реализующей эту функцию, имеется функциональное соответствие. Однако, поскольку одна и та же функция может быть выражена различными формулами, ее реализация неоднозначна. Всегда можно построить много различных логических схем, соответствующих данной логической функции. Такие схемы называют эквивалентными.
Из множества эквивалентных схем можно выделить наиболее экономичную или хотя бы достаточно простую схему путем упрощения формулы, соответствующей данной функции. Обычно принято считать более простыми те формулы, которые содержат меньшее количество вхождений переменных и символов логических операций.
Задача упрощения аналитических выражений решается в конкретном базисе с помощью тождественных преобразований. Чаще всего эту задачу связывают с базисом, состоящим из отрицания, дизъюнкции и конъюнкции, который будем называть булевым базисом. После того как формула выражена через основные операции, она упрощается на основании тождеств булевой алгебры, приведенных в (2. 1).
Например, функция из (3) упрощается следующим образом: 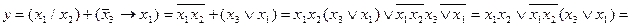
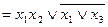 .
.
5. Минимальные формы. Как было показано в (2. 3), любая булева функция представима в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Более того, такое представление является первым шагом перехода от табличного задания функции к ее аналитическому выражению. В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получаются на основе принципа двойственности (2. 1).
Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т. е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний). Такие формы называют минимальными. При каноническом синтезе предполагается, что на входы схемы подаются как сигналы х i , так и их инверсии `xi. Формула, представленная в дизъюнктивной нормальной форме, упрощается многократным применением операции склеивания 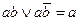 и операций поглощения
и операций поглощения 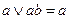 и
и 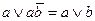 (дуальные тождества для конъюнктивной нормальной формы имеют вид:
(дуальные тождества для конъюнктивной нормальной формы имеют вид: 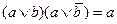 ;
; 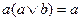
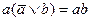 ). Здесь под a и b можно понимать любую формулу булевой алгебры. В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются уже невозможными, т. е. получаем тупиковую форму. Среди тупиковых форм находится и минимальная дизъюнктивная форма, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма является минимальной, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.
). Здесь под a и b можно понимать любую формулу булевой алгебры. В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются уже невозможными, т. е. получаем тупиковую форму. Среди тупиковых форм находится и минимальная дизъюнктивная форма, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма является минимальной, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.
Пусть, например, функция задана в совершенной нормальной дизъюнктивной форме:  . Группируя члены и применяя операцию склеивания, имеем
. Группируя члены и применяя операцию склеивания, имеем 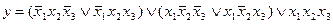 . При другом способе группировки
. При другом способе группировки 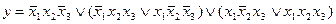 . Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, так как
. Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, так как 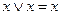 ). В первом случае таким членом может быть
). В первом случае таким членом может быть 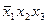 . Тогда
. Тогда 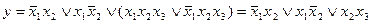 . Добавив член
. Добавив член 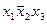 , получим:
, получим: 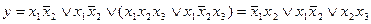 . Перебрав все возможные варианты, можно убедиться, что две последние формы являются минимальными.
. Перебрав все возможные варианты, можно убедиться, что две последние формы являются минимальными.
Работа с формулами на таком уровне подобна блужданию в потемках. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать некоторые графические и аналитические представления и специально разработанную для этой цели символику.
6. Многомерный куб. Каждой вершине n-мерного куба (1. 9), можно поставить в соответствие конституенту единицы (2, 5). Следовательно, подмножество отмеченных вершин является отображением на n-мерном кубе булевой функции от п переменных в совершенной дизъюнктивной нормальной форме. На рис. 21 показано такое отображение для функции из (5).
Для отображения функции от п переменных, представленной в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитермами (2. 2) и элементами n-мерного куба.
Минитерм (n - 1)-го ранга  можно рассматривать как результат склеивания двух минитермовn-го ранга (конституент единицы), т. е.
можно рассматривать как результат склеивания двух минитермовn-го ранга (конституент единицы), т. е. 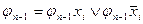 .На n-мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координаты xi, соединяющим эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины). Таким образом, минитермам (n - 1)-го порядка соответствуют ребра n-мерного куба. Аналогично устанавливается соответствие минитермов (п - 2)-го порядка граням n-мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
.На n-мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координаты xi, соединяющим эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины). Таким образом, минитермам (n - 1)-го порядка соответствуют ребра n-мерного куба. Аналогично устанавливается соответствие минитермов (п - 2)-го порядка граням n-мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
 |  |

Элементы n-мерного куба, характеризующиеся s измерениями, называют s -кубами. Так, вершины являются 0-кубами, ребра - 1-кубами, грани - 2-кубами и т. д. Обобщая приведенные рассуждения, можно считать, что Минитерм (п - s)-го ранга в дизъюнктивной нормальной форме для функции п переменных отображается s-кубом, причем каждый s-куб покрывает все те s-кубы низшей размерности, которые связаны только с его вершинами. В качестве
примера на рис. 22 дано отображение функции трех переменных 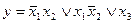 .Здесь минитермы
.Здесь минитермы  и
и  соответствуют 1-кубам (s = 3 – 2 = 1), а минитерм
соответствуют 1-кубам (s = 3 – 2 = 1), а минитерм 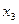 отображается 2-кубом (s = 3 - 1 = 2).
отображается 2-кубом (s = 3 - 1 = 2).
Итак, любая дизъюнктивная нормальная форма отображается на n-мерном кубе совокупностью s-кубов, которые покрывают все вершины, соответствующие конституентам единицы (0-кубы). Справедливо и обратное утверждение: если некоторая совокупность s-кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим s-кубам минитермов является выражением данной функции в дизъюнктивной нормальной форме. Говорят, что такая совокупность s-кубов (или соответствующих им минитермов) образует покрытие функции.
Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число s-кубов которого было бы поменьше, а их размерность s - побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием. Например, для функции из (5) покрытие на рис. 23, а соответствует неминимальной форме 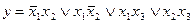 ,а покрытия на рис. 23, б и в - минимальным формам
,а покрытия на рис. 23, б и в - минимальным формам 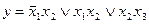 и
и 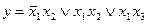 .
.
Отображение функции на n-мерном кубе наглядно и просто при п 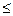 3. Четырехмерный куб можно изобразить, как показано на
3. Четырехмерный куб можно изобразить, как показано на
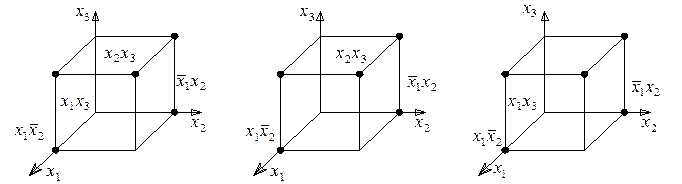
а б в
Рис. 23. Покрытие функции  :
:
а – неминимальное; б, в – минимальное.
рис. 24, где отображены функция четырех переменных и ее минимальное покрытие, соответствующие выражению  . Использование этого метода при п > 4 требует настолько сложных построений, что теряются все его преимущества.
. Использование этого метода при п > 4 требует настолько сложных построений, что теряются все его преимущества.
Рис. 24. Отображение функции 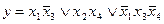 на
на
четырехмерном кубе
7. Карты Карно. В другом методе графического отображения булевых функций используются карты Карно, которые представляют собой специально организованные таблицы соответствия.
Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причемэти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладаютэтимсвойством. Как и в обычных таблицах соответствия (1. 3), клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписывают, им соответствуют пустые клетки). Для упрощения строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно s-кубу соответствует совокупность 2 соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике (с учетом соседства противоположных краев карты). Поэтому все положения, изложенные в (6), справедливы и для карт Карно.
Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие s-куб, дают минитерм (n - s)-го ранга, в который входят те (n - s) переменные, которые сохраняют одинаковые значения на этом s-кубе, причем значениям 1 соответствуют сами переменные, а значениям 0 - их отрицания. Переменные, которые не сохраняют свои значения на s-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в дизъюнктивной нормальной форме.
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае четырех переменных. Для отображения функций пяти переменных используются две карты Карно на четыре переменные, а для функций шести переменных - четыре таких карты. При дальнейшем, увеличении числа переменных карты Карно становятся практически непригодными.
Известные в литературе карты Вейча отличаются только другим порядком следования наборов значений переменных и обладают теми же свойствами, что и карты Карно.
8. Комплекс кубов. Несостоятельность графических методов при большом числе переменных компенсируется различными аналитическими методами представления булевых функций. Одним из таких представлений является комплекс кубов, использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой.
Комплекс кубов K (у) функции у = f (х1, х2, ..., х n ) определяется как объединение множеств Ks (у) всех ее s-кубов (s = 0, 1, .... n), т. е. 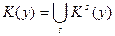 , причем некоторые из Ks( у ) могут быть пустыми. Для записи s-кубов и минитермов функции от п переменных используются слова длины п, буквы которых соответствуют всем n переменным. Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен единице (1 для xi и 0 для
, причем некоторые из Ks( у ) могут быть пустыми. Для записи s-кубов и минитермов функции от п переменных используются слова длины п, буквы которых соответствуют всем n переменным. Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен единице (1 для xi и 0 для  ). Не входящие в минитерм переменные являются свободными и обозначаются через х. Например, 2-куб функции пяти переменных, соответствующий минитерму
). Не входящие в минитерм переменные являются свободными и обозначаются через х. Например, 2-куб функции пяти переменных, соответствующий минитерму  , запишется как (x10x1). 0-кубы, соответствующие конституентам единицы, представляются наборами значений переменных, на которых функция равна единице. Очевидно, в записи s-куба всегда имеется s свободных переменных. Если все п переменных свободны, что соответствует n-кубу, то это означает тождественность единице рассматриваемой функции. Таким образом, для функций, не равных тождественно единице,
, запишется как (x10x1). 0-кубы, соответствующие конституентам единицы, представляются наборами значений переменных, на которых функция равна единице. Очевидно, в записи s-куба всегда имеется s свободных переменных. Если все п переменных свободны, что соответствует n-кубу, то это означает тождественность единице рассматриваемой функции. Таким образом, для функций, не равных тождественно единице,  .
.
Множество всех s-кубов К(у) записывается как совокупность слов, соответствующих каждому s-кубу. Для удобства будем располагать слова s-кубов в столбцы, а их совокупность заключать в фигурные скобки. Например, комплекс кубов, соответствующий представлению функции на трехмерном кубе (рис. 219, а), выражается как  , где
, где
 ;
; 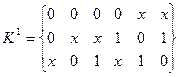 ;
; 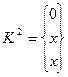
Комплекс кубов образует максимальное покрытие функции. Исключая из него все те s-кубы, которые покрываются кубами высшей размерности, получаем покрытия, соответствующие тупиковым формам. Так, для рассматриваемого примера имеем тупиковое покрытие
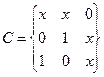
которое соответствует  . В данном случае это покрытие являетcя и минимальным.
. В данном случае это покрытие являетcя и минимальным.
Для двух булевых функций операция дизъюнкции соответствует объединению их комплексов кубов 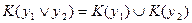 , а операция конъюнкции - пересечению комплексов кубов
, а операция конъюнкции - пересечению комплексов кубов 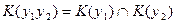 .Отрицанию функции соответствует дополнение комплекса кубов, т. е.
.Отрицанию функции соответствует дополнение комплекса кубов, т. е. 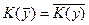 , причем
, причем 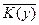 определяется всеми вершинами, на которых функция принимает значение 0. Таким образом, имеет место взаимно-однозначное соответствие (изоморфизм) между алгеброй булевых функций и алгеброй множеств, представляющих комплексы кубов.
определяется всеми вершинами, на которых функция принимает значение 0. Таким образом, имеет место взаимно-однозначное соответствие (изоморфизм) между алгеброй булевых функций и алгеброй множеств, представляющих комплексы кубов.
Представление функций в виде комплексов кубов менее наглядно, однако его важнейшие достоинства состоят в том, что снимаются ограничения по числу переменных и облегчается кодирование информации при использовании вычислительных машин.
9. Реализация в различных формах. Реализация функции в дизъюнктивной нормальной форме представляет собой логическую схему И-ИЛИ. Например, функция  реализуется логической схемой. Более экономичная реализация получается, если общий множитель вынести за скобки:
реализуется логической схемой. Более экономичная реализация получается, если общий множитель вынести за скобки: 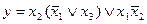 . При использовании элементов со многими входами получаем двухуровневую логическую схему И—ИЛИ.
. При использовании элементов со многими входами получаем двухуровневую логическую схему И—ИЛИ.
В соответствии с принципом двойственности (2.1), заменяя в дизъюнктивной нормальной форме операции конъюнкции на дизъюнкции, операции дизъюнкции на конъюнкции и беря отрицание каждой переменной, получаем конъюнктивную нормальную форму, которая выражает функцию 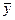 , обратную к у. Ее реализация с помощью многовходовых элементов представляет собой двухуровневую логическую схему ИЛИ—И. Для рассматриваемой функции
, обратную к у. Ее реализация с помощью многовходовых элементов представляет собой двухуровневую логическую схему ИЛИ—И. Для рассматриваемой функции  соответствующая реализация показана на рис. 26, г . Если требуется получить схему для данной функции у, то используется инвертор или элемент, реализующей операцию НЕ—И.
соответствующая реализация показана на рис. 26, г . Если требуется получить схему для данной функции у, то используется инвертор или элемент, реализующей операцию НЕ—И.
Конъюнктивную нормальную форму можно получить и другим путем. Для этого используются рассуждения и методы, дуальные рассмотренным по отношению к дизъюнктивным нормальным формам. На многомерном кубе ищется покрытие множества вершин для нулевых значений функции, а на карте Карно - покрытие нулевых клеток. Рассматриваемый пример иллюстрируется на рис. 221, а и б. Соответствующая конъюнктивная нормальная форма 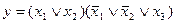 реализуется соответствующей схемой. Комплекс кубов этой функции и его дополнение имеют вид:
реализуется соответствующей схемой. Комплекс кубов этой функции и его дополнение имеют вид:
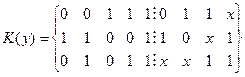 ;
; 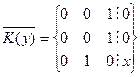 ,
,
а их покрытия
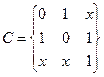 ;
; 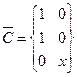 .
.
Покрытию С соответствует дизъюнктивная нормальная форма для отрицания функции 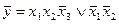 , откуда можно получить приведенное выше выражение функции в конъюнктивной нормальной форме.
, откуда можно получить приведенное выше выражение функции в конъюнктивной нормальной форме.
10. Многовыходные схемы. Схемы, реализующие несколько функций, можно представить как простое объединение схем, реализующих каждую функцию отдельно. Но такой путь, как правило, является неэкономичным. Часто бывает целесообразно преобразовать совокупность данных функций к такому виду, чтобы реализующие их схемы содержали общие части, а схема с многими выходами представляла собой единое целое.
Задача сводится к выбору для каждой функции такого покрытия, которое включало бы возможно большее число s-кубов, содержащихся в покрытиях других функций. Этому требованию удовлетворяют, например, покрытия для трех функций, которому соответствует трехвыходная схема. Если бы для функции y 3 было выбрано другое покрытие, то схема получилась бы менее экономичной.
В этом параграфе описаны различные методы представления булевых функций применительно к задаче минимизации. При небольшом числе переменных эта задача обозрима, и ее можно решить простым перебором различных вариантов. Для функции многих переменных разработаны формальные методы минимизации, которые рассматриваются в следующем параграфе.
11. Постановка задачи. Минимизация схемы в булевом базисе сводится к поиску минимальной дизъюнктивной формы, которой соответствует минимальное покрытие. Общее число букв, входящих в нормальную форму, выражается ценой покрытия 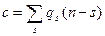 - число s-кубов, образующих покрытие даннойфункции от п переменных. Используются и другие определения цены покрытия, например с’ = с + q , где q - общее число всех кубов покрытия. Во всех случаях минимальное покрытие характеризуется наименьшим значением его цены.
- число s-кубов, образующих покрытие даннойфункции от п переменных. Используются и другие определения цены покрытия, например с’ = с + q , где q - общее число всех кубов покрытия. Во всех случаях минимальное покрытие характеризуется наименьшим значением его цены.
Обычно задача минимизации решается в два шага. Сначала ищут сокращенное покрытие, которое включает все s-кубы максимальной размерности, но не содержит ни одного куба, покрывающегося каким-либо кубом этого покрытия. Соответствующую дизъюнктивную нормальную форму называют сокращенной, а ее минитермы - простыми импликантами. Для данной функции сокращенное покрытие является единственным, но оно может быть избыточным вследствие того, что некоторые из кубов покрываются совокупностями других кубов.
На втором шаге осуществляется переходот сокращенной к тупиковым дизъюнктивным' нормальным формам, из которых выбираются минимальные формы. Тупиковые формы образуются путем исключения из сокращенного покрытия всех избыточных кубов, без которых оставшаяся совокупность кубов еще образует покрытие данной функции, но при дальнейшем исключении любого из кубов она уже не покрывает множества всех вершин, соответствующих единичным значениям функции, т. е. перестает быть покрытием.
Куб сокращенного покрытия, который покрывает вершины данной функции, не покрываемые никакими другими кубами, не может оказаться избыточным и всегда войдет в минимальное покрытие. Такой куб, как и соответствующая ему импликанта, называют экстремалью (существенной импликантой), а покрываемые им вершины—отмеченными вершинами. Множество экстремалей образует ядро покрытия. Ясно, что при переходе от сокращенного покрытия к минимальному прежде всего следует выделить все экстремали. Если множество экстремалей не образует покрытия, то оно дополняется до покрытия кубами из сокращенного покрытия.
Сокращенное покрытие Z, и минимальные покрытия С’ min и C ” min выражаются следующим образом:
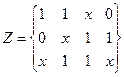 ;
; 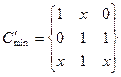 ;
; 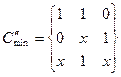 .
.
Сокращенная форма представляет собой дизъюнкцию четырех простых импликант, т. е. 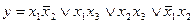 . Экстремалями являются простые импликанты
. Экстремалями являются простые импликанты  и
и  , которым соответствуют 1-кубы (10x) и (01x), а отмеченные вершины -
, которым соответствуют 1-кубы (10x) и (01x), а отмеченные вершины - 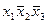 и
и 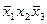 или соответственно (100) и (010).
или соответственно (100) и (010).
2. Метод Квайна - Мак-Класки. Этот метод используется в случаях, когда функция задана в дизъюнктивной совершенной нормальной форме (или таблицей соответствия). Приведение к сокращенной форме осуществляется последовательным применением операции склеивания  , где a - конъюнкции переменных, отличных от xi . Множеству конституент единицы, представленных в исходной форме, соответствует совокупность 0-кубов K 0, а операции склеивания - объединение двух 0-кубов, которые отличаются только одной координатой. Результатом такого объединения является 1-куб, в котором различные координаты исходных 0-кубов замещены символом х. Сравнивая попарно все 0-кубы, получаем множество 1-кубов K 1. Применяя к K 1 операцию склеивания, находим множество 2-кубов K 2 и т. д. Этот процесс продолжается до тех пор, пока получаемое из Ks очередное Ks +1 не окажется пустым множеством. В результате множество K 0 преобразуется в комплекс кубов К = { K 0 , K 1 , K 2 , …, Ks ], причем
, где a - конъюнкции переменных, отличных от xi . Множеству конституент единицы, представленных в исходной форме, соответствует совокупность 0-кубов K 0, а операции склеивания - объединение двух 0-кубов, которые отличаются только одной координатой. Результатом такого объединения является 1-куб, в котором различные координаты исходных 0-кубов замещены символом х. Сравнивая попарно все 0-кубы, получаем множество 1-кубов K 1. Применяя к K 1 операцию склеивания, находим множество 2-кубов K 2 и т. д. Этот процесс продолжается до тех пор, пока получаемое из Ks очередное Ks +1 не окажется пустым множеством. В результате множество K 0 преобразуется в комплекс кубов К = { K 0 , K 1 , K 2 , …, Ks ], причем 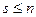 .
.
Для выделения из К множества простых импликант 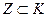 при каждой операции склеивания необходимо отмечать каким-либо знаком (например, меткой
при каждой операции склеивания необходимо отмечать каким-либо знаком (например, меткой  ) те кубы, которые объединяются в кубы высшей размерности. Очевидно, неотмеченные кубы и образуют множество простых импликант Z. Чтобы уменьшить число сравниваемых пар при операции объединения целесообразно разбить множество Ks на классы, в каждом из которых содержатся s-кубы с одинаковым числом единиц (или нулей), и упорядочить эти классы по возрастающему числу единиц. Так как объединяться могут только такие два s-куба, число единиц в которых точнонаодну больше или меньше, то достаточно ограничиться попарным сравнением s-кубов одного класса с s-кубами соседнего класса.
) те кубы, которые объединяются в кубы высшей размерности. Очевидно, неотмеченные кубы и образуют множество простых импликант Z. Чтобы уменьшить число сравниваемых пар при операции объединения целесообразно разбить множество Ks на классы, в каждом из которых содержатся s-кубы с одинаковым числом единиц (или нулей), и упорядочить эти классы по возрастающему числу единиц. Так как объединяться могут только такие два s-куба, число единиц в которых точнонаодну больше или меньше, то достаточно ограничиться попарным сравнением s-кубов одного класса с s-кубами соседнего класса.
На втором шаге при извлечении экстремалей и образовании минимального покрытия используется таблица покрытий. Ее строки соответствуют простым импликантам, а столбцы — конституентам единицы дизъюнктивной совершенной нормальной формы данной функции, которые представляются 0-кубами (вершинами) комплекса кубов. В клетку таблицы записывается метка, если простая импликанта в данной строке покрывает вершину в данном столбце. Экстремалям соответствуют те строки таблицы, которые содержат единственную метку в каком-либо столбце. Удаляя строки экстремалей и все столбцы, в которых эти строки имеют метки, получаем более простую таблицу. На основе этой таблицы выбираем простые импликанты, которые дополняют выделенное множество экстремалей до минимального покрытия функции.
3. Пример минимизации функции. Рассмотрим в качестве примера функцию четырех переменных у = f (х1, х2, х3, х4), заданную таблицей соответствия
Ей соответствует дизъюнктивная совершенная нормальная форма 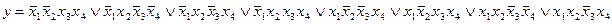 . Множество 0-кубов после разбиения и упорядочения записывается следующим образом:
. Множество 0-кубов после разбиения и упорядочения записывается следующим образом:
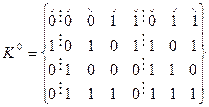 .
.
Объединяя кубы и отмечая те из них, которые покрываются кубами большей размерности, имеем:
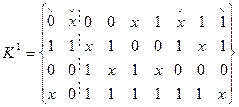 ;
;  .
.
Простым импликантам соответствуют неотмеченные кубы.Составляем таблицу покрытия Z, которому соответствует сокращенная форма 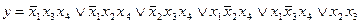 .
.
| K0 Z | 0 1 0 0 | 0 0 1 1 | 0 1 0 1 | 1 0 0 1 | 1 1 0 0 | 0 1 1 1 | 1 0 1 1 | 1 1 0 1 | Обозначения импликант |
| 0 x 1 1 | 
| 
| A | ||||||
| 0 1 x 1 | 
| 
| B | ||||||
| x 0 1 1 | 
| 
| C | ||||||
| 1 0 x 1 | 
| 
| D | ||||||
| 1 x 0 1 | 
| 
| E | ||||||
| x 1 0 x | 
| 
| 
| 
| F |
Извлекаем единственную экстремаль (х10х), которой соответствует минитерм 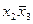 и упрощаем таблицу к виду:
и упрощаем таблицу к виду:
| K0 Z | 0 0 1 1 | 1 0 0 1 | 0 1 1 1 | 1 0 1 1 |
| 0 x 1 1 | 
| 
| ||
| 0 1 x 1 | 
| |||
| x 0 1 1 | 
| 
| ||
| 1 0 x 1 | 
| 
| ||
| 1 x 0 1 | 
|
В качестве дополнительных целесообразно выбрать кубы (0x11) и (10x1), так как они совместно с экстремалью (x10x) образуют покрытие функции, минимальная форма которой имеет вид:  . Соответствующее этой функции минимальное покрытие иллюстрируется на четырехмерном кубе и на карте Карно.
. Соответствующее этой функции минимальное покрытие иллюстрируется на четырехмерном кубе и на карте Карно.
7. Частично определенные функции. В практике нередко приходится иметь дело с такими функциями, которые определены не на всех наборах значений переменных. Подобные случаи встречаются, когда по условиям функционирования некоторые из наборов не используются и поэтому безразлично, какие значения принимает функция на этих наборах. Это обстоятельство можно использовать при минимизации функции, доопределив ее на безразличных наборах так, чтобы обеспечить наиболее экономичную реализацию.
Пусть дана частично определенная функция у1 = f 1(x 1, х2, …, х n). Обозначим через у1 = f 1(x 1, х2, …, х n) функцию, которая доопределена на всех безразличных наборах единицами, а через у0 = f 0(x 1, х2, …, х n) - нулями. Задача оптимального доопределения данной функции сводится к выбору из сокращенного покрытия для функции у1 минимального количества кубов максимальной размерности, совокупность которых покрывала бы все вершины функции y 0. Такая совокупность кубов и образует минимальное покрытие частично определенной функции у. При этом оно может покрывать и некоторые вершины, соответствующие безразличным наборам, что означает доопределение функции на этих наборах единичными значениями.
Дата добавления: 2022-01-22; просмотров: 33; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!