Одномерное движение идеальных жидкости и газа

Гидрогазодинамика

Методические указания к практическим занятиям

для студентов направления подготовки 13.03.01 «Теплоэнергетика и

           теплотехника», профиля «Энергообеспечение предприятий»

 

 

санкт-петербург

2021

УДК 519.86:622.3.012 (073)

 

ГИДРОГАЗОДИНАМИКА: Методические указания к практическим занятиям. Санкт-Петербургский горный университет. Сост. Е.М.Ротинян, СПб, 2021.  40 с.

 

Методические указания предназначены для подготовки и выполнения студентами практических заданий. Содержат необходимые сведения и порядок выполнения типовых практических заданий, а также задания на практические занятия.

 Предназначены для студентов дневной формы обучения студентов направления подготовки 13.03.01 «Теплоэнергетика и теплотехника», профиля «Энергообеспечение предприятий»

 

 

Научный редактор:   проф. В.А. Лебедев

 

Рецензент:

 

ÓСанкт-Петербургский

горный университет, 2021

ВВЕДЕНИЕ

Целью практических занятий является закрепление теоретических знаний, полученных студентом при изучении курса, и использовании этих знаний при решении задач на производстве.

Задачей практических занятий является ознакомление студентом с частными вопросами разного характера в области гидрогазодинамики, как базовой науки для изучения и расчета тепловых машин и теплоэнергетического оборудования предприятий.

Физические свойства жидкостей

 

Термин «жидкость» в ГГД применяется как к газам, так и к капельным жидкостям.

Жидкость, рассматриваемая в ГГД, считается сплошной (непрерывной) средой. Средняя длина свободного пробега молекул жидкости должна на несколько порядков меньше характерного линейного размера рассматриваемого жидкого объёма. Иначе говоря, в элементарном объёме жидкости, который называют ещё жидкой частицей, должно содержаться очень много молекул.

Плотность жидкости ρ определяется через предельное отношение массы Δm, заключённой в объёме ΔV, включающем нашу точку, когда этот объём стремится к нулю: 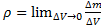 . Средняя по объёму плотность определяется тем же равенством, только без предельного перехода. Размерность плотности: [ρ]=кг/м³. Для несжимаемой жидкости ρ= const.

Обратная плотности величина – удельный объём 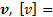 м³/кг. В технике используют также понятие удельный вес – произведение плотности на ускорение свободного падения: γ=ρ· g, Н/м³. Давление р в международной системе единиц СИ измеряют в Па (используются также кратные и несистемные единицы: атм (физическая атмосфера), ат (техническая атмосфера), мм вод.ст., мм рт.ст., бар и др.), температура – в Кельвинах [Т]=К, или в градусах Цельсия [t]=^оС .

Если рассматривается газ, близкий по свойствам к идеальному, используется термическое уравнение состояния – уравнение Клапейрона – Менделеева, записанное обычно через плотность:

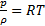 ,                                    (1.1)

R = R ₀ / μ [Дж/(кг К)] – индивидуальная газовая постоянная, 

R ₀ =8314 [Дж/(кмоль К)] – универсальная газовая постоянная,  

μ [кг/кмоль] – мольная (молярная) масса газа;

и калорическое уравнение состояние:

dh = c_p ∙ dt,                                    (1.2)

h [Дж/кг]  – удельная энтальпия, c_p [Дж/(кг К)]  – удельная массовая изобарная теплоёмкость.

Газ, теплоёмкость которого принимается постоянной, в ГГД называется совершенным; для совершенного газа:

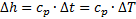.                              (1.2а)

 

Способность жидкости (газа) под действием внешнего давления изменять свой объём (плотность) называется сжимаемостью. Сжимаемость характеризуется коэффициентами 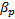 и .

И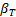зотермический коэффициент сжимаемости 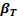 характеризует относительное изменение объёма жидкости при изменении давления при постоянной температуре:

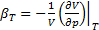 .                            (1.3)

 Для большинства жидкостей  β _T =10^-9…10^-10 1/Па. 

Коэффициент теплового объёмного расширения 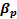 (часто обозначается просто β) характеризует относительное изменение объёма при изменении температуры при постоянном давлении:

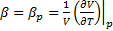.                           (1.4)

Как правило, жидкости и газы расширяются с повышением температуры, а их плотность при этом уменьшается. Исключением является жидкая вода: при изменении температуры от 0^оС до 4^оС её плотность возрастает, достигая максимума при 4^оС, а при дальнейшем повышении температуры начинает уменьшаться. Для воды при нормальных условиях β _p =1.5 ·10^-4 1/К.

Для газов:

 β _p =1/Т, β _T =1/р.                              (1.5)

Величину, обратную к изотермическому коэффициенту сжимаемости, называют модулем упругости: Е=1/ β _T, Па. Для воды при нормальных условиях Е=2.25·10⁹ Па.

 

Силы, рассматриваемые в ГГД, являются распределёнными и по природе действия длятся на массовые (или объёмные) –  действуют на все точки жидкой частицы одинаково (силы тяжести, инерции, электромагнитные, центробежные) и поверхностные – действуют в узком поверхностном слое, на поверхности соприкосновения выделенного жидкого объёма с другими объёмами или с твёрдой стенкой (силы давления, трения, в том числе внутреннего, поверхностного напряжения, сопротивления).

Если на элементарную площадку ΔS действует поверхностная сила 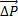, то напряжение поверхностной силы:

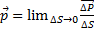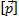, =Па.

Если на элементарный объём ΔV действует массовая сила 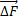, то

плотность распределения массовой силы:

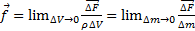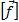 , =Н/кг=м/с²;

по сути, 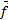 – это ускорение.

 

В покоящейся жидкости поверхностные силы направлены по внутренней нормали к элементу поверхности (статическое давление). В движущейся вязкой жидкости имеются и нормальные и касательные составляющие поверхностных сил (силы трения).

 

Жидкость, лишённая вязкости, называется идеальной жидкостью. В идеальной жидкости отсутствуют касательные компоненты поверхностной силы (касательные напряжения). Нормальное напряжение в идеальной жидкости не зависит от ориентации площадки, к которой приложено и называется гидростатическим давлением p .

 

Для простейшего сдвигового течения (скорость направлена по оси х: w_x = w; изменение скорости есть только по оси y) касательное напряжение τ  определяется законом трения Ньютона:

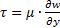.                                    (1.6)

μ – коэффициент динамической вязкости, [μ]=Па·с. 

Несистемная единица измерения динамической вязкости называется пуаз: 1 пз=0.1 Па·с.

Из закона трения Ньютона следует, что в покоящейся жидкости вязкость как физическое свойство есть, но при этом вязкое трение отсутствует.

Часто важно знать напряжение трения на границе твёрдой стенки и обтекающей её жидкости (при y=0). Напряжение трения на стенке обычно обозначают индексом «w»:

.

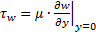Жидкости, напряжение трения в которых описывается законом трения Ньютона (1.6), и скорость которых на твёрдой стенке равна нулю: 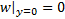 (удовлетворяющие условию «прилипания» на стенке), называются ньютоновскими.

Жидкости, которые не удовлетворяют закону трения Ньютона, называются неньютоновскими или реологическими. К неньютоновским жидкостям относятся густые нефти, буровые растворы, масляные краски, смесь крахмала с водой и всевозможные суспензии, например, зыбучие пески или кровь.

 

Динамическая вязкость газов с ростом температуры увеличивается, жидкостей – уменьшается. Вязкость – свойство реальной жидкости, в идеальной жидкости μ=0.

Для аппроксимации коэффициента динамической вязкости газов применяются степенные формулы вида:

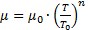  ,                               (1.7)

или более точную формулу Сазерленда:

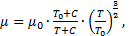                             (1.8)

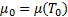, T - абсолютная температура, С – константа.

 

Отношение коэффициента динамической вязкости к плотности называется коэффициентом кинематической вязкости:    

ν= μ/ ρ,                                  (1.9) 

[ν]=м²/с; несистемная единица измерения: стокс: 1 ст=10^-4 м²/с.

 

Для аппроксимации коэффициентов динамической и кинематической вязкостей жидкостей применяются формулы вида:

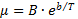  ,                               (1.10)

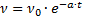  ,                               (1.11)

B , b, a – постоянные для данной жидкости величины;

T - температура в Кельвинах, t – температура в градусах Цельсия, .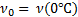

       Для расчёта коэффициента динамической вязкости воды применяют эмпирическую формулу Пуазейля:

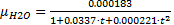   .                               (1.12)

 

Задачи к разделу 1

1.1. Для масла известны значения коэффициентов динамической вязкости при двух температурах: μ₁ = μ(t ₁) и μ₂ = μ(t ₂).Найти константы зависимости (1.10) и определить μ₃ при температуре t ₃.

Варианты приведены в табл.1.

                                                       Таблица 1

№	Марка масла	t1		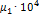t2		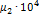t3	№	Марка масла	t1		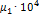t2		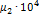t3
		0С	Па∙с	0С	Па∙с	0С			0С	Па∙с	0С	Па∙с	0С
1	Транс- форма- торное	0	629.8	100	21.3	50	16	Масло МК	10	35414	150	56.90	60
2		20	198.2	100	21.3	60	17		10	35414	140	70.34	70
3		10	335.5	100	21.3	70	18		20	18560	130	87.31	80
4		40	89.4	120	15.7	80	19		20	18560	120	110.4	90
5		30	128.5	110	18.1	90	20		30	6180	110	145.2	60
6		10	335.5	100	21.3	80	21		30	6180	100	202.1	70
7		20	198.2	110	18.1	70	22		40	3031	110	145.2	80
8	Масло  МС-20	20	10026	110	132.4	60	23		40	3031	120	110.4	90
9		20	10026	150	53.17	70	24		50	1638	130	87.31	60
10		30	4670	110	132.4	80	25		50	1638	140	70.34	70
11		30	4670	140	61.8	90	26		10	35414	80	399.3	100
12		40	2433	120	101.0	100	27		20	18560	80	399.3	110
13		40	2433	130	79.76	90	28		30	6180	90	273.7	120
14		50	1334	110	132.4	80	29		40	3031	90	273.7	130
15		50	1334	150	53.17	70	30		50	1638	80	399.30	140

 

1.2. Опытным путём установлено, что для одного из сортов нефти при t ₁ =3^оС ν₁=3.6 ст, при t ₂ =10^оС ν₂=2.1 ст. Установить константы ν₀ и а  зависимости (1.11) и найти кинематическую вязкость этой нефти при t ₃ =6^оС.

1.3. Для сухого воздуха задаться коэффициентом динамической вязкости μ₀ =17.2∙10^-6 Па∙с при температуре t ₀ =0^оС  и μ₁ =49.0∙10^-6 Па∙с при температуре t ₁ =1000^оС. Найти константы зависимостей (1.7) и (1.8), затем по этим формулам определить коэффициент динамической вязкости воздуха при температуре t  и относительную погрешность каждой из формул, сравнив полученные расчётные значения с табличным значением μ(t) при этой температуре. Табличные свойства воздуха взять из приложения. Температуру t выбрать из табл.2.

                                                     Таблица 2

№	t	№	t	№	t	№	t	№	t	№	t
	0С		0С		0С		0С		0С		0С
1	-50	6	10	11	60	16	120	21	250	26	500
2	-40	7	20	12	70	17	140	22	300	27	550
3	-30	8	30	13	80	18	160	23	350	28	600
4	-20	9	40	14	90	19	180	24	400	29	650
5	-10	10	50	15	100	20	200	25	450	30	700

 

1.4. Автоклав с диаметром и длиной цилиндрической части d=1 м и l=2 м соответственно имеет днище и крышку в форме полусфер. Определить дополнительный объём воды 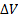, который нужно закачать в автоклав, чтобы давление поднялось от р₀=1 бар до давления р=1001 бар. Изотермический коэффициент сжимаемости  .

 

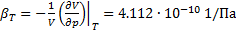1.5. Предполагая, что температура и солёность морской воды не меняются с глубиной, вычислить её удельный вес γ на глубине, где гидростатическое давление составляет 100 ати (избыточных технических атмосфер). На поверхности удельный вес γ₀=10084.68 Н/м³, изотермический коэффициент сжимаемости .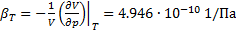

 

1.6. Определить силу поверхностного трения тонкой пластинки длиной L =1 ми шириной  b=1.5 м, с двух сторон обтекаемой воздухом, если известно, что на расстоянии 0.5 мм от поверхности пластины скорость воздуха составляет w=2 м/с, и что изменение скорости воздуха на таких расстояниях от стенки можно приближённо считать линейным; температура воздуха t _ж=20^оС.

При решении использовать условие «прилипания» для скорости на стенке; свойства воздуха взять из приложения.

 

1.7. Определить поверхностное напряжение на поверхности движущегося судна и оценить скорость его движения, если изменение скорости воды w по нормали к поверхности выражается уравнением  w( y )= a ∙ y - b ∙ y ², справедливым при y ≤δ. Температура воды t _ж. Данные взять из табл.3; свойства воды – из приложения.

Использовать условие «прилипания» на стенке и считать, что на расстояниях, больших δ, скорость практически перестаёт меняться.

                                                     Таблица 3

№	tж	а	b	δ	№	tж	а	b	δ
	0С	1/с	1/(с∙м)	мм		0С	1/с	1/(с∙м)	мм
1	10	200	2500	10	16	15	510	4700	38
2	10	220	2600	10	17	15	520	8000	35
3	10	240	2700	12	18	15	520	8250	32
4	10	260	2800	13	19	5	400	8500	33
5	10	280	2900	15	20	5	420	8750	34
6	10	300	3000	20	21	5	450	9000	35
7	20	325	3200	22	22	5	475	9250	30
8	20	350	3300	25	23	5	500	9500	40
9	20	375	3500	25	24	5	510	9750	44
10	20	400	3600	28	25	5	510	10000	25
11	20	420	3700	30	26	25	290	2900	21
12	20	450	3800	32	27	25	300	3000	22
13	15	475	4000	30	28	25	310	3000	23
14	15	500	4300	33	29	25	320	3100	24
15	15	510	4500	35	30	25	330	3200	25

Статика

 

Основное уравнение статики, выражающее условие равновесия массовых и поверхностных сил (получено Л.Эйлером в 1755 г.):

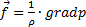 .                          (2.1)

В декартовой системе координат (ДСК) плотность распределения массовой силы (ускорение этой силы):

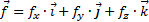                      (2.2)

Основное уравнение статики в проекциях на оси ДСК:

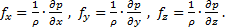             (2.3)

 

Вторая форма записи основного уравнения статики:

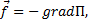                                     (2.4)

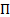 - потенциал массовой силы (если сила – это сила тяжести,  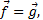то 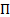 - удельная потенциальная энергия);

Эта форма записи означает, что для равновесия жидкости массовые силы, действующие в ней, должны быть потенциальны.

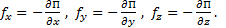             (2.5)

Знак «минус» показывает, что потенциал возрастает в направлении, противоположном действию силы (если сила тяжести направлена вниз, то потенциальная энергия возрастает с увеличением высоты).

 

       Третья форма записи основного уравнения статики:  

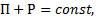                                    (2.6)

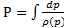 - функция давления, выражает условие баротропности.

Функция давления определена с точностью до константы (как потенциал массовой силы):

.

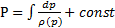Можно записать иначе:

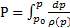.                               (2.7)

Значение константы в этом случае задаётся значением при р₀ – обычно это нормальные условия, т.е. t ₀ =0^оС, р₀=760 мм рт. ст., ρ₀=ρ (р₀).

 

Баротропными называются процессы, в которых плотность зависит только от давления: ρ= ρ(р).

Среди процессов с идеальным газом баротропными являются изотермический, обратимый адиабатный (изоэнтропийный), изохорный (процесс с постоянной плотностью) и политропный при n≠0.

Функция давления для баротропных процессов с идеальным газом:

 

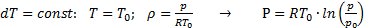;       (2.8)

 

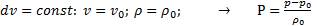                     (2.9)                                 

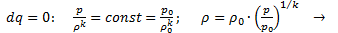
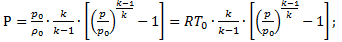       (2.10)

               

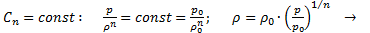
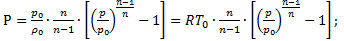       (2.11)

 

 

Для равновесия несжимаемой жидкости под действием силы тяжести из основного уравнения статики получаем закон Паскаля: 

p = p ₀ +ρ gz .                                     (2.12)

Давление на глубине погружения z складывается из давления на свободной поверхности p ₀ и давления столба жидкости.

Для равновесия сжимаемого газа (баротропной атмосферы) получаем в случае изотермической атмосферы:

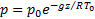,                            (2.13)

z- высота поднятия над уровнем моря;

в случае адиабатной атмосферы:

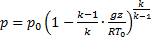;        (2.14)

в случае политропной атмосферы:

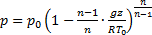.            (2.15)

       К задачам статики традиционно относят также задачи на применение закона Архимеда: на тело, погруженное в жидкость (газ) действует выталкивающая сила, равная весу жидкости в объёме тела.

 

Задачи к разделу 2

2.1. Имеются две жидкости с плотностями ρ₁ и ρ₂ , залитые послойно в ёмкость, как показано на рис.1а. Над свободной поверхностью верхней жидкости находится воздух плотностью ρ₀ (ρ₀<ρ₁<ρ₂). Затем в ёмкость осторожно опускают до касания с верхней жидкостью твёрдое тело, отпускают его и дожидаются, пока тело перестанет двигаться в жидкости и остановится, _.как показано на рис.1б. Плотность тела  ρ.

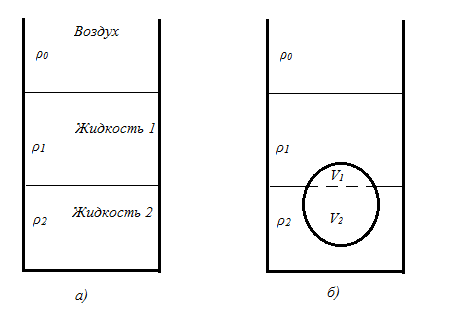
Рис.1. К задаче 2.1

Как соотносятся плотности жидкостей и тела, если оно плавает так, как показано на рис.1б?

Нарисовать, где будет находиться тело, если:

1)  ρ= ρ₀,  2) ρ₀< ρ< ρ₁, 3) ρ= ρ₁, 4)   ρ₁< ρ< ρ₂, 5)  ρ=ρ₂, 5)  ρ>ρ₂?

Для рис.1б определить , какая часть тела находится в первой жидкости, какая – во второй, т.е. найти V ₁ / V , V ₂ / V , где V - общий объём тела.

 

2.2. Тело, имеющее форму круглого конуса, плавает в жидкости, как показано на рис.2. Определить глубину погружения z, если известны высота конуса Z, удельные веса жидкости γ_ж и материала тела γ (табл.4). Задачу решить двумя способами: 1) пренебрегая выталкивающей силой, действующей на конус со стороны воздуха; 2) учитывая эту силу и приняв удельный вес воздуха γ₀= 12 Н/м³.

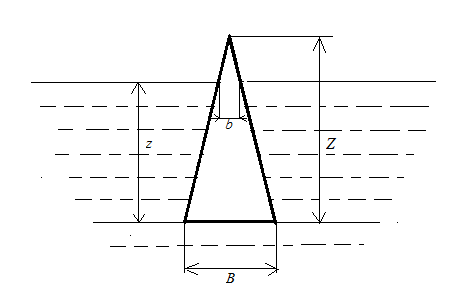
Рис.2. К задаче 2.2

                                                      Таблица 4

№	γж	γ	Z	№	γж	γ	Z	№	γж	γ	Z
	Н/м3	Н/м3	м		Н/м3	Н/м3	м		Н/м3	Н/м3	м
1	9810	6000	1.	11	8850	5950	0.35	21	8440	6200	1.4
2	9800	6000	0.9	12	8800	5950	0.45	22	8460	6300	1.5
3	9810	5900	0.8	13	8750	5900	0.55	23	8480	6400	1.45
4	9800	5500	0.7	14	8700	5850	0.65	24	8500	6500	1.35
5	9760	5500	0.6	15	8650	5800	0.75	25	8520	6600	1.25
6	9750	5600	0.5	16	8600	5750	0.85	26	8535	6500	1.35
7	9740	5700	0.4	17	8550	5700	0.95	27	8555	6600	1.25
8	9730	5700	0.3	18	8500	5650	1.1	28	8655	5500	1.15
9	9720	5600	0.2	19	8400	6000	1.2	29	8455	5500	1.1
10	8900	6000	0.25	20	8420	6100	1.3	30	8255	5000	1.

2.3. Две несмешивающиеся жидкости залиты в U-образный манометр, как показано на рис.3а. На свободных поверхностях жидкостей давление одинаково и равно атмосферному. Известны высоты поднятия жидкостей относительно границы раздела z ₁ и z ₂ .

Найти соотношение между плотностями жидкостей. Какая жидкость тяжелее?

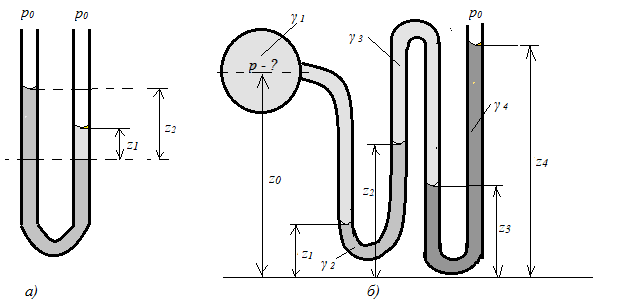
Рис.3. К задачам 2.3 и 2.4

 

2.4. Для измерения давления р в сосуде применён многоколенчатый жидкостной манометр (рис.3б), в который послойно залиты жидкости с удельными весами γ ₁, γ ₂, γ ₃, γ ₄. Известны все высоты z ₁ , z ₂ , z ₃ , z ₄ , z ₀ и атмосферное давление на свободной поверхности р₀. Выразить давление р. В чём преимущество такого манометра перед обычными U-образными? Каковы недостатки?

 

2.5. Пояснить, как получено правило пересчёта давления из мм вод. ст. в Па: 1 мм вод.ст.=g Па≈9.81 Па. Определить плотность ртути, если для ртути правило пересчёта давления: 1 мм рт.ст.=133.3 Па.

Какие изменения давления позволяют определять водяной и ртутный манометры, если считать, что глаз определяет колебания уровня жидкости в 1 мм?

 

2.6. U-образный жидкостной манометр наклонили под углом α и подсоединили к трубе, по которой движется поток воздуха, как показано на рис.4. Определить статическое давление воздуха в трубе, если известно атмосферное давление р₀=750 мм рт.ст., плотность жидкости, залитой в манометр, и разность уровней жидкости Δl в коленах наклонного манометра. Данные содержатся в табл.5.

 

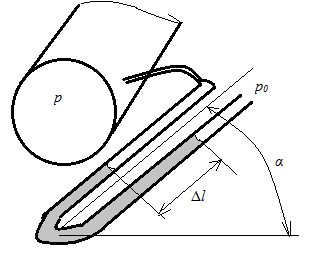
Рис.4. К задаче 2.6

                                                      Таблица 5

№	α	ρ	Δl	№	α	ρ	Δl	№	α	ρ	Δl
	град.	кг/м3	мм		град.	кг/м3	мм		град.	кг/м3	мм
1	20	1000	20	11	25	900	55	21	30	800	66
2	25	990	25	12	30	890	55	22	35	1100	22
3	30	980	30	13	35	880	48	23	40	1200	24
4	35	970	35	14	40	870	47	24	45	1300	26
5	40	960	40	15	45	860	36	25	50	1400	28
6	45	950	40	16	50	850	38	26	60	770	30
7	50	940	35	17	55	840	37	27	50	780	35
8	55	930	35	18	60	830	44	28	40	790	40
9	60	920	50	19	20	820	54	29	30	760	45
10	20	910	50	20	25	810	58	30	20	750	50

 

2.7. Распределение давления и плотности в земной атмосфере в зависимости от высоты над уровнем моря представлено в табл. 6. Это т.н. стандартная атмосфера – усреднённые по широте экспериментальные значения.

1) Рассчитать отношения давлений p / p ₀ на тех же высотах в изотермической и адиабатной атмосферах.

2) Предположив, что земная атмосфера является политропной, проверить это предположение при помощи данных табл.6 и найти показатель политропы n.   

Параметры «0»: p ₀ = 760 мм рт.ст. , ρ ₀=1.225 кг/м³ , Т₀=288.15 К; газовая постоянная воздуха R=287 Дж/(кг К).

 

                       Таблица 6

z	p / p 0	ρ /ρ0
м	-	-
-2000	1.26112	1.20666
-1000	1.12441	1.09966
0	1	1
500	0.94213	0.952876
1000	0.887010	0.907477
2000	0.784618	0.821676
3000	0.692042	0.742248
5000	0.533415	0.601166
10000	0.261533	0.337559
20000	0.054570	0.072579

 

 

2.8. В ёмкость, имеющую форму круглого цилиндра радиусом R, стоящую на горизонтальной поверхности, налита жидкость плотностью ρ. Уровень жидкости в неподвижном цилиндре составляет z ₀ . Затем цилиндр вместе с водой приводят во вращение вокруг вертикальной оси, совпадающей с осью цилиндра. Угловая скорость вращения ω= const.  Минимальная высота поднятия жидкости во вращающемся цилиндре z (на оси), максимальная высота поднятия Z (на стенке), как показано на рис.5. Стенки цилиндра достаточно высоки, чтобы жидкость не выплёскивалась при вращении.

1) Найти угловую скорость вращения ω. Данные взять из табл.7.

2) Определить форму свободной поверхности жидкости.

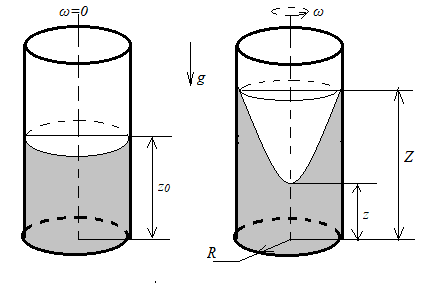
Рис.5. К задаче 2.8

                                                      Таблица 7

№	ρ	R	z 0	z	Z	№	ρ	R	z 0	z	Z
	кг/м3	мм	мм	мм	мм		кг/м3	мм	мм	мм	мм
1	1000	50	-	20	50	16	800	70	60	-	80
2	1000	60	-	10	60	17	1300	75	50	-	80
3	990	60	-	30	60	18	1300	80	70	-	90
4	990	40	-	40	50	19	1100	85	70	-	80
5	990	50	-	35	70	20	1100	90	80	-	100
6	980	60	-	25	70	21	1200	95	80	-	120
7	980	55	-	30	80	22	1200	100	90	-	110
8	950	65	-	35	80	23	900	50	90	-	120
9	950	70	-	25	90	24	900	60	80	-	90
10	950	85	-	30	90	25	900	70	85	-	115
11	999	80	-	40	80	26	985	50	-	60	120
12	999	90	-	50	85	27	985	50	-	50	120
13	999	90	-	40	90	28	985	60	-	55	110
14	800	60	50	-	70	29	955	60	-	50	100
15	800	65	60	-	75	30	995	55	-	40	100

 

Использовать при решении соотношение: z ₀ =(Z + z)/2. Вывести его, приравнивая объёмы неподвижной и вращающейся жидкости.

 

2.9. Измеритель ускорения, установленный на электровозе, представляет собой U-образный манометр, заполненный водой. Расстояние между вертикальными трубками (коленами) манометра составляет l= 200 мм. Определить ускорение движущегося горизонтально электровоза, если разность уровней воды в коленах составляет ∆ z=100 мм.

Одномерное движение идеальных жидкости и газа

 

Используемая в гидравлике модель одномерного движения предполагает, что все параметры меняются только вдоль одной координаты, в общем случае криволинейной, и, возможно, от времени: 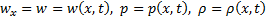 для сжимаемой жидкости и т.д. Рассматривается трубчатая поверхность – жидкая струя, окружающая ось течения. Перпендикулярное оси сечение площадью 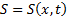называется живым сечением.

 Для установившегося (стационарного) движения .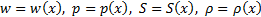

 

Уравнение неразрывности, выражающее закон сохранения массы, для стационарного одномерного движения имеет вид:

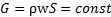;                                 (3.1)

G, [кг/с] –массовый расход,

S,[м²] - площадь поперечного сечения.

Если дополнительно принять, что жидкость несжимаема: ρ= const, получим:

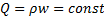 .                               (3.2)

 Q, [м³/с] - объёмный расход.

Уравнения энергии для одномерного стационарного движения без подвода извне теплоты и работы в дифференциальной и интегральной формах, соответственно, имеет вид:

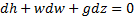,                            (3.3а)

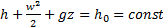,                  (3.3б)

h, 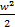, gz [Дж/кг] - удельные энтальпия, кинетическая и потенциальная энергии,  

z [м]– вертикальная координата; расстояние от некоторого выбранного уровня отсчёта до оси струи (оси трубы).

Для газов часто пренебрегают изменением потенциальной энергии, тогда дифференциальная и интегральная формы уравнения энергии:

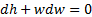,                            (3.4а)

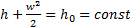,                          (3.4б)

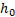 называется энтальпией торможения (энтальпией заторможенного потока); выражает запас энергии газа в энергоизолированном потоке.

Для идеального совершенного газа можно записать:

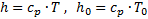,                       (3.5)

Т₀ – температура торможения.

 

Уравнение Бернулли выражает баланс механической энергии, в одномерном движении совпадает с уравнением сохранения количества движения.

Дифференциальная форма уравнения Бернулли для стационарного движения при отсутствии внешних сил:

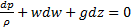.                     (3.6)

Для течения сжимаемого газа интегральная форма:

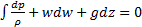,                      (3.7а)

где первое слагаемое представляет собой функцию давления Р, второе – удельную кинетическую энергию, а третье – потенциал массовой силы – силы тяжести, т.е. удельная потенциальная энергия.

Часто для газа пренебрегают потенциальной энергией и записывают:  

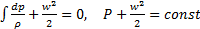.         (3.7б)

Для несжимаемой жидкости получаем интеграл Бернулли:

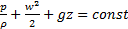.                      (3.8)

Все слагаемые в этом интеграле имеют размерность удельной работы (удельной энергии), таким образом, сумма  работы сил давления, кинетической и потенциальной энергий вдоль направления движения для стационарного режима при отсутствии внешних сил не меняется.  

Сумма статического р  и динамического 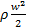давлений называется полным давлением:

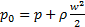 .                                   (3.9)

 

Интеграл Бернулли также может быть записан «в терминах» высот:  

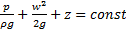 .                        (3.10)

Сумма пьезометрической высоты (пьезометрического напора) 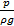, динамической высоты (напора)  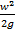 и нивелирной высоты  вдоль потока для стационарного режима при отсутствии внешних сил и трения постоянна.

 

 

Задачи к разделу 3

 

3.1. Из большого открытого бака через маленькую дырочку в днище вытекает идеальная жидкость. Уровень жидкости в баке Z. Оценить скорость истечения жидкости. Реальная скорость истечения больше или меньше полученного оценочного значения? Как будет меняться скорость вытекания жидкости из отверстия со временем?

 

3.2. Горизонтальный канал прямоугольного сечения с высокими стенками в основной части имеет ширину b ₁ и глубину потока z₁, средняя скорость течения воды при этом составляет w ₁. В канале имеется участок местного сужения шириной b ₂. Пренебрегая потерями на трение, найти глубину потока z ₂ и скорость w ₂ в узкой части. Данные взять из табл.8.

                                                      Таблица 8

№	b 1	z 1	w1	b2	№	b 1	z 1	w1	b2	№	b 1	z 1	w1	b2
	м	м	м/c	м		м	м	м/c	м		м	м	м/c	м
1	12	3	0.5	8	11	14	4	0.5	10	21	9	3.5	0.5	5
2	12	4	0.45	7	12	14	4	0.4	11	22	9	4.5	0.6	5
3	11	5	0.5	6	13	13	3.5	0.5	10	23	13	4	0.5	10
4	11	4	0.4	7	14	13	3.5	0.4	9	24	13	4.5	0.45	9
5	10	4	0.5	6	15	9	4	0.5	5	25	12	4	0.6	9
6	10	3	0.5	7	16	9	3	0.6	4	26	11	3.5	0.45	7
7	12	4	0.6	8	17	15	3	0.5	10	27	10	5.5	0.45	6
8	12	4.5	0.6	9	18	15	3	0.55	9	28	11	4.5	0.4	6
9	11	4.5	0.65	8	19	10	5	0.4	6	29	10	4.5	0.5	6
10	11	4.5	0.65	9	20	10	4	0.5	5	30	10	3.5	0.5	7

3.3. Струя воды из фонтана бьёт на высоту Z от места вытекания. Фонтан имеет форму вертикального усечённого круглого конуса, обращённого вверх малым сечением. Диаметр конуса внизу, у основания, D,  вверху, в месте вытекания воды, d, высота конуса z. Определить объёмный расход воды, подаваемой к фонтану Q , а также избыточное давление у основания фонтана. Данные взять из табл.9.

                                               Таблица 9

№	D	d	z	Z	№	D	d	z	Z	№	D	d	z	Z
	мм	мм	м	м		мм	мм	м	м		мм	мм	м	м
1	50	10	0.5	8	11	50	10	0.8	8	21	55	25	0.5	9
2	45	10	0.5	8	12	50	10	0.85	8.5	22	55	20	0.6	8.5
3	40	10	0.5	7.5	13	60	15	0.6	9	23	55	25	0.6	9
4	60	20	0.5	7.5	14	60	15	0.65	9	24	55	20	0.5	8.5
5	65	20	0.5	7	15	60	15	0.5	9	25	55	25	0.55	9
6	70	25	0.5	7	16	60	15	0.55	8	26	65	25	0.7	8
7	50	10	0.6	8	17	60	15	0.5	8	27	65	30	0.7	8
8	50	10	0.65	8.5	18	60	15	0.65	8	28	65	25	0.65	8
9	50	10	0.7	8	19	60	15	0.6	7	29	65	20	0.6	7
10	50	10	0.75	8.5	20	60	15	0.65	7	30	65	20	0.55	7

 

3.4. По горизонтальной круглой трубе переменного сечения протекает идеальная жидкость с удельным весом γ=10⁴ Н/м³ с объёмным расходом Q=1 литр/с. Диаметры сечений 1 и 2 составляют соответственно d ₁ =100 мм и d ₂=25 мм. Каким должно быть давление в сечении 1, чтобы в сечении 2 образовался вакуум?

 

3.5. В аэродинамической трубе, предназначенной для разгона воздуха до больших дозвуковых скоростей (рис.6), давление в широкой части (форкамера, сечение 1) измеряется вертикальным спиртовым манометром, который показывает Δ z =280 мм сп. ст.; плотность спирта ρ_сп=800 кг/м³. В узкой части (рабочая область, сечение 2) давление измеряется наклонным ртутным манометром (угол наклона α=30^о), который показывает Δ l=692 мм рт. ст. Температура в форкамере t₁=17^оС, давление в помещении, где находится труба, р₀=98066 Па. Степень поджатия (отношение площадей сечений форкамеры и рабочей области) S ₁ / S ₂=5. Не учитывая потери и предполагая, что течение воздуха в трубе можно считать адиабатическим, найти в сечении 1: ρ₁ и w ₁, в сечении 2: ρ₂, w ₂ , t ₂. Индивидуальная газовая постоянная воздуха R= 287 Дж/(кг∙К), показатель адиабаты (изоэнтропы) воздуха k=1.4.

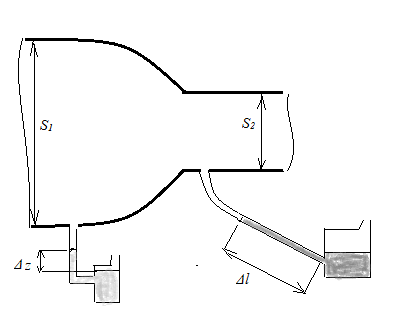
Рис.6. К задаче 3.5

 

Одномерная газовая динамика

Газ будем считать идеальным совершенным.

Термическое уравнение состояния - уравнение Клапейрона – Менделеева:

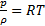 ,                                       (4.1)  

Калорическое уравнение состояния:

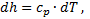                                     (4.2)

теплоёмкости постоянны и определяются по формулам молекулярно – кинетической теории:

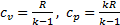,                           (4.3)

показатель адиабаты (изоэнтропы):

k=5/3≈1.67  - для одноатомных газов;

k=1.4       - для двухатомных газов (включая воздух, как смесь в                                                           основном двухатомных газов);

k=4/3≈1.33  - для трёх- и многоатомных газов.

 

Параметры изоэнтропийно заторможенного потока (параметры торможения) обозначаются индексом «0»:  .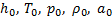

Процесс распространения малых возмущений (звуковых волн) в газе будем считать адиабатным.

Скорость звука в газах, близких к идеальным, пропорциональна корню из абсолютной температуры:

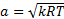                       (4.4)

Сечение, в котором скорость потока равна местной скорости звука, называется критическим. Критические параметры обозначаются индексом «*».

Критическая скорость звука определяется соотношением:

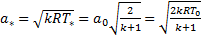.             (4.5)

 

Максимальная скорость, до которой может разогнаться газ, соответствует, формально, остыванию до абсолютного нуля:

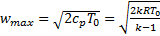 .                  (4.6)

Эта скорость «теоретическая», достижению её в реальном газе мешает конденсация и трение.

 

Отношение скорости потока к местной скорости звука называется числом Маха:

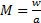.                               (4.7)

В идеальном газе число Маха меняется в диапазоне:

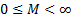.                              (4.8)

 

Отношение скорости потока к критической скорости звука называется скоростным коэффициентом λ:

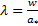.                                (4.9)

В идеальном газе диапазон изменения скоростного коэффициента:

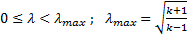.              (4.10)

В критическом сечении М=λ=1 (звуковое течение). В дозвуковом течении М<1, λ<1; в сверхзвуковом М>1, λ>1.

 

Число Маха и скоростной коэффициент связаны соотношением:

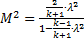 .                           (4.11)

 

Из уравнения энергии: 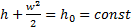 с использованием уравнений изоэнтропы в разных парах термических переменных получают формулы, связывающие безразмерные скорость звука, температуру, плотность, давление и расход потока с безразмерной скоростью в данном сечении.

Если эти формулы записаны через число Маха, их называют изоэнтропийными формулами, если они записаны через скоростной коэффициент - газодинамическими функциями:

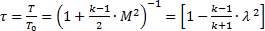,                            (4.12)  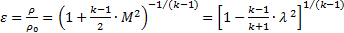                            ,           (4.13)                      

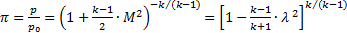,          (4.14)                          

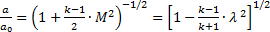,                               (4.15)                                             

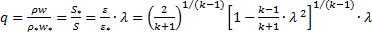.   (4.16)                 

последним соотношением определяется безразмерный массовый расход или функция тока.

       Температура, плотность, давление и скорость звука обезразмериваются на максимальное значение – параметр в сечении торможения. Функция тока, поскольку в сечении торможения скорость потока равна нулю, обезразмеривается на параметры в критике.

       Значения газодинамических функций в критике получаются подставлением в соотношения (4.12) – (4.19) М=1 или λ=1:

,

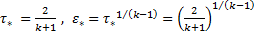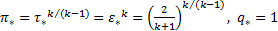.             (4.17)

 

Для удобства использования формулы (4.11) – (4.16) часто реализуют в виде таблиц газодинамических функций: задают с некоторым шагом скоростной коэффициент λ (например, λ=0, λ=0.01, λ=0.02, …) и, используя правую часть формул, рассчитывают τ(λ), ε(λ), π(λ), q(λ), а также М(λ).

Таблицами удобнее пользоваться, если известным является не скоростной коэффициент, а любой другой параметр: безразмерное давление π, плотность ε, и особенно функция тока q (как отношение площадей критического и текущего сечений).

По известному значению параметра в соответствующем столбце таблицы определяются все остальные параметры в строчке.

Нужно только иметь в виду, что τ(λ), ε(λ), π(λ), М(λ) – однозначные функции, т.е. каждому значению параметра соответствует только одна строчка в таблице, а функция тока q(λ) – двухзначная, т.е. значению q=0.5, например, соответствуют две строчки в таблице: одна на дозвуке, вторая – на сверхзвуке.

Вид таблицы газодинамических функций приведён ниже (табл.10).

                                          Таблица 10

( k=1.4)	λ	τ	ε	π	q	М
Дозвук	0	1	1	1	0	0
	0.01	…	…	…	…	…
	0.02	…	…	…	…	…
	...	…	…	…	…	…
	…	…	…	…	…	…
	…	…	…	…	…	…
Критика	1	τ*	ε*	π*	1	1
Сверхзвук	1.01	…	…	…	…	…
	1.02	…	…	…	…	…
	…	…	…	…	…	…
	…	…	…	…	…	…
	…	…	…	…	…	…
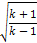
		0	0	0	0	∞

 

           

 

Шаг по λ, равный 0.01, как правило, является достаточным для решения задач, если же нужны более точные решения, можно составить таблицы с меньшим шагом, например, 0.005.

 

       При движении тела в газовой среде со сверхзвуковой скоростью возмущения, вносимые телом, лежат внутри конуса Маха (рис.7). За пределами конуса Маха лежит зона тишины.

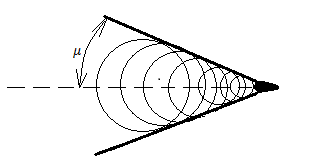
Рис.7. Конус Маха

 

Угол между образующей конуса и направлением движения тела называется углом Маха μ,

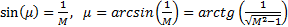 . (4.18)

Образующие конуса – это линии Маха или характеристики.

       Если отсутствует трение и передача теплоты и работы через стенки канала (адиабатное течение идеального газа), то управление скоростью потока в канале осуществляется путём изменения площади сечения. Математически это описывается уравнением Гюгонио:

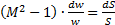 .                      (4.19)

В дозвуковом течении скорость потока будет увеличиваться при уменьшении площади поперечного сечения канала:

,

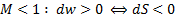В сверхзвуковом течении, напротив, для дальнейшего увеличения скорости потока нужно расширять канал:

.

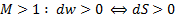Критическое сечение (звуковой режим течения), если оно есть, совпадает с минимальным сечением канала.

       Максимальная скорость, которая может быть получена на выходе суживающегося сопла - конфузора, - звуковая, ей соответствует критическое безразмерное давление на выходе .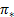

Скорость в любом сечении суживающегося сопла может быть рассчитана по входным параметрам торможения (если считать, что истечение происходит из большого бака) по формуле Сен-Венана-Ванцеля:

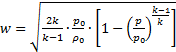 ,                   (4.20)

безразмерный массовый расход (функция тока) – по формуле:

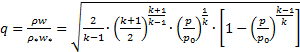.  (4.21)

При уменьшении давления на выходе (противодавления) происходит разгон потока. Если противодавление становится меньше критического, наступает явление «запирания сопла»: истечение будет происходить с постоянной (критической) скоростью, несмотря на дальнейшее понижение давления.

Максимально возможный расход газа через суживающееся сопло:

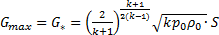 ,            (4.22)

где S - площадь выходного сечения.

       Расход в любом сечении 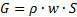  можно выразить также через параметры торможения – давление и температуру, функцию тока и постоянный множитель b=b ( k , R ):

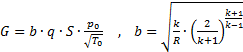 . (4.23)

Выражение (4.22) получается из (4.23) при подстановке q=1.

Задачи к разделу 4

 

4.1. Составить (см. табл. 10) таблицу газодинамических функций для двухатомных газов, выбрав в качестве параметра скоростной коэффициент λ, с шагом 0.005. Сохранить её для решения задач этого и последующих разделов.

 

4.2. Наблюдатель на земле зарегистрировал звук пролетающего самолёта через 2.5 секунды после того, как самолёт находился вертикально над наблюдателем. Известно, что высота полёта 1 км. Атмосферная температура на этой высоте составляет Т=281.5 К. Считая, что температура по высоте меняется слабо, оценить скорость самолёта. Если учитывать, что на самом деле температура у поверхности земли больше, чем на высоте 1 км, как это повлияет на результат?

 

4.3. Плотность воздуха в некотором объёме была ρ₁, а после изоэнтропийного сжатия стала ρ₂. Оценить относительное изменение плотности (ρ₂-ρ₁)/ρ₁, если известно, что скорость прохождения звуковой волны в сжатом воздухе стала на 3% больше.

4.4. Из баллона со сжатым азотом вылетает струя газа со скоростью, равной половине от максимально возможной теоретической скорости. Температура газа в баллоне равна 300 К. Найти число Маха М и скоростной коэффициент λ. Расчёт провести с использованием формул и проверить по таблице из задачи 4.1.

4.5. Найти максимальную скорость, до которой можно разогнать газ из состояния покоя с температурой t₀, если пренебречь внутренним трением (вязкостью) газа. Известно, что газ сжижается при температуре t_кип. Разгон газа считать адиабатическим. Данные взять в табл.11.

                                         Таблица 11

№	Газ	t0	t кип	№	Газ	t0	t кип
		0С	0С			0С	0С
1	O2	50	-182.96	16	H2	50	-252.87
2	O2	20	-182.96	17	F2	0	-188.12
3	O2	25	-182.96	18	F2	20	-188.12
4	O2	15	-182.96	19	F2	30	-188.12
5	CO	20	-191.5	20	Cl2	25	-34.55
6	CO	30	-191.5	21	Cl2	50	-34.55
7	CO	50	-191.5	22	Cl2	40	-34.55
8	N2	50	-195.75	23*	CO2	10	-78
9	N2	75	-195.75	24*	CO2	30	-78
10	N2	100	-195.75	25*	CO2	50	-78
11	Воздух	0	-185.15	26	Ar	100	-185.85
12	Воздух	100	-185.15	27	Ar	120	-185.85
13	Воздух	200	-185.15	28	Ar	110	-185.85
14	H2	0	-252.87	29	Ar	130	-185.85
15	H2	25	-252.87	30	Ar	150	-185.85

 

 

(*) – для двуокиси углерода указанная в последнем столбце температура является температурой сублимации, поскольку газообразный СО₂ переходит в твёрдую фазу, минуя жидкую.

 

4.6. Из воздухопровода заводской магистрали через насадок в форме круглого усечённого конуса происходит истечение воздуха в атмосферу (рис.8). Диаметр выходного сечения конуса d, параметры торможения воздуха:  p₀ и T₀, атмосферное давление 1 бар. Найти скорость истечения и массовый расход воздуха через патрубок. Если уменьшить давление торможения в два раза, изменится ли скорость истечения? Изменится ли расход? Данные взять из табл.12.

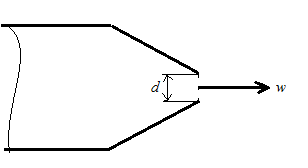
Рис.8. К задаче 4.6

                                           Таблица 12

№	p0	t0	d	№	p0	t0	d	№	p0	t0	d
	МПа	0С	мм		МПа	0С	мм		МПа	0С	мм
1	0.2	50	10	11	0.7	150	20	21	0.5	110	24
2	0.25	20	10	12	0.75	170	20	22	0.4	80	22
3	03	40	16	13	0.8	180	22	23	0.3	90	24
4	0.35	25	12	14	0.85	100	22	24	0.2	50	26
5	0.4	60	14	15	0.9	150	20	25	1.0	200	28
6	0.45	100	16	16	0.95	155	16	26	0.5	30	16
7	0.5	170	10	17	0.9	200	14	27	0.6	40	18
8	0.55	150	18	18	0.8	210	12	28	0.7	50	16
9	0.6	110	20	19	0.7	205	10	29	0.8	60	20
10	0.65	120	18	20	0.6	220	20	30	0.9	70	22

 

4.7. Построить график зависимости безразмерного массового расхода 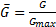 при истечении через суживающееся сопло от безразмерного противодавления  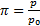для двухатомного газа. Можно использовать как формулы, так и таблицу газодинамических функций.

 

4.8. Построить график зависимости числа Маха от скоростного коэффициента М=М(λ) и график зависимости λ = λ(М),  используя формулу (4.11) либо таблицу. Сделать вывод о возможности замены М на λ и наоборот в качестве характеристики течения в дозвуковом, гиперзвуковом и сверхзвуковом потоке.

 

Скачок уплотнения

 

      При адиабатном торможении сверхзвукового потока идеального газа каждое малое изменение параметров вызывает образование звуковой волны, причём каждая последующая волна идёт по всё более сжатому (и горячему) газу, а значит, скорость её больше, чем у предыдущей. Это приводит к тому, что волны малых возмущений догоняют друг друга, складываются и образуют мощную ударную волну – скачок уплотнения. Скачки разрежения в идеальном газе не реализуются. Скачок уплотнения является поверхностью разрыва – параметры потока при переходе через скачок резко меняются на расстоянии, примерно равном длине свободного пробега молекул (доли микрона). Важно понимать, что скачок уплотнения, даже в идеальном газе, не является изоэнтропийным явлением!

      Если поверхность разрыва (фронт скачка) нормальна к скорости потока, скачок называют прямым, если наклонена под острым углом – косым. Совокупность прямого и системы косых скачков образует криволинейный скачок уплотнения.

 

За скачком уплотнения скорость падает, температура, давление и плотность растут, температура торможения не меняется: Т₀₁=Т₀₂, а давление и плотность торможения уменьшаются, что объясняется необратимыми потерями механической энергии.

Для вывода соотношений на прямом скачке уплотнения удобно систему координат привязать к фронту скачка, и считать, что на неподвижную линию скачка натекает сверхзвуковой поток газа (параметры «1»), а за скачком течение дозвуковое (параметры «2»).

 

Скорости на прямом скачке связывает формула Прандтля:

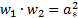или 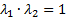.                (5.1)

 

Соотношение, связывающее давления и плотности на скачке, называют ударной адиабатой Гюгонио: 

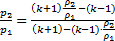                        (5.2)

График ударной адиабаты имеет асимптоту: 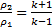 в отличие от адиабаты Пуассона 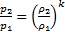, асимптот не имеющей.

       Отношение давлений торможения на прямом скачке равно отношению плотностей торможения и может быть вычислено по формуле:

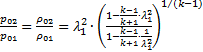 .            (5.3)

 

Косой скачок уплотнения возникает, например, когда сверхзвуковой газовый поток обтекает тело с заострённой носовой частью. Считая обтекание симметричной, можно рассматривать обтекание потоком клина с углом ω (рис.9). Угол наклона фронта скачка к исходному направлению потока – угол скачка- обозначен β.

 

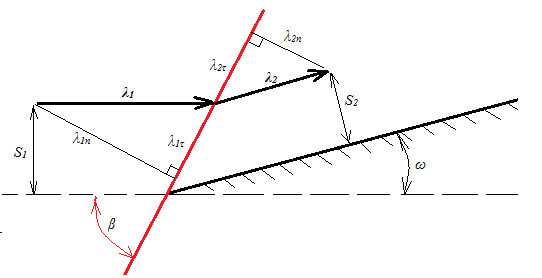
Рис.9. Косой скачок уплотнения на клине

Косой скачок можно разложить на прямой скачок для проекции скорости на направление, нормальное к фронту скачка (λ_{2 n} =1/λ_{1 n}), и отсутствие изменений для проекции скорости на направление, касательное к фронту скачка (λ_1τ=λ_2τ). Соотношения, полученные для прямого скачка, сохраняют силу, но для нормальных к фронту составляющих скоростей. Общее изменение параметров на косом скачке всегда слабее, чем на прямом с теми же параметрами «1». Чаще косой скачок происходит со сверхзвука на меньший сверхзвук (поэтому возможна последовательность из нескольких косых скачков, пока течение остаётся сверхзвуковым), тогда как прямой скачок всегда переводит сверхзвуковое течение в дозвуковое.

Связь числа Маха М₁ набегающего потока, угла клина ω и угла скачка β задаётся формулой:

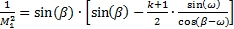.       (5.4)

В этом уравнении угол клина и число Маха набегающего потока – известные параметры, угол скачка – определяемая величина. Обычно решение уравнения (5.4) представляют в виде графика, на котором каждому М₁ соответствует своя параметрическая кривая (рис.10).

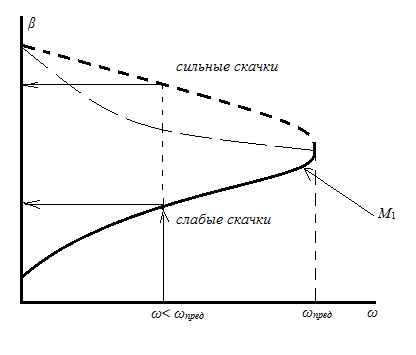
Рис.10. Графическое решение уравнения (5.4)

Уравнение (5.4) имеет два корня, из которых выбирается меньший, т.е. реализуется всегда «слабый» косой скачок, с меньшим углом наклона β, с меньшим изменением параметров и, соответственно, с меньшими потерями.

Для каждого М₁ существует предельное значение угла клина ω_пред, при котором скачок ещё присоединён к носику клина и имеет прямолинейную линию фронта. При ω> ω_пред скачок сходит с клина, и образуется отошедшая ударная волна с криволинейным фронтом; для этого случая формула (5.4) и соотношения для скоростей на скачке, приведённые выше, несправедливы.

 

Задачи к разделу 5

5.1. Используя формулу (5.2), построить графики ударных адиабат Гюгонио для одно-, двух- и трёхатомного газов, задав 5-6 значений ρ₂/ρ₁. Для сравнения на том же графике построить график адиабаты Пуассона (изоэнтропийное сжатие). Что можно сказать о той части графика ударной адиабаты, которая соответствует значениям ρ₂/ρ₁<1?

 

5.2. В идеальном одноатомном газе произошёл прямой скачок уплотнения. Известно, что перед скачком скорость газа была максимально возможной: λ₁=λ_max. Найти λ₁, λ₂, а также отношение плотностей на скачке ρ₂/ρ₁.

 

5.3. По известному отношению плотностей на скачке и температуре торможения Т₀ (табл.13) найти скоростные коэффициенты λ₁ и λ₂, размерные скорости до и после скачка w₁ и w₂, а также отношение давлений торможения 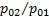. Идеальный газ обладает свойствами воздуха. Решить задачу с помощью формул; сравнить с решением, полученным с использованием таблицы газодинамических функций из задачи (4.1).

                                           Таблица 13

№	ρ2/ρ1	Т0	№	ρ2/ρ1	Т0	№	ρ2/ρ1	Т0
1	5.4	1000	11	3.8	850	21	4.3	750
2	5.3	1000	12	3.6	850	22	4.5	700
3	5.2	1000	13	3.4	950	23	4.7	700
4	5.1	900	14	3.2	950	24	4.9	700
5	5.0	900	15	3.0	950	25	2.9	700
6	4.8	900	16	3.3	1050	26	5.5	900
7	4.6	800	17	3.5	1050	27	4.55	900
8	4.4	800	18	3.7	1050	28	3.55	1000
9	4.2	800	19	3.9	750	29	2.55	1000
10	4.0	850	20	4.1	750	30	5.55	800

 

 

5.4. Входные кромки профилей сверхзвуковой компрессорной решётки выполнены в виде одинаковых заострённых клиньев, чтобы избежать отсоединённых скачков уплотнения, вызывающих большие потери энергии. На рис.11 показаны два соседних элемента решётки; в поперечном к плоскости изображения измерении клинья достаточно длинные, чтобы можно было считать задачу плоской. Торможение сверхзвукового потока во входной части межлопаточного канала в этом случае происходит в системе косых скачков уплотнения, которые замыкаются, как правило,  слабым прямым скачком. Для упрощения задачи систему из нескольких косых скачков, расходящихся веером от носика клина, заменим одним косым скачком. Правее фронта косого скачка (линия АВ) параметры потока – входные (область 1). После косого скачка (левее линии АВ) поток имеет параметры «2» (область 2). Если поток остался сверхзвуковым, т.е. 1<M₂<M₁ и 1<λ₂<λ₁), то там, где фронт косого скачка касается поверхности следующего клина (точка В), происходит прямой скачок (его фронт – линия ВС, перпендикулярная поверхности клина). После замыкающего прямого скачка поток приобретает параметры «3»; M₃<1, λ₃<1 (область 3). Дальнейшее торможение потока, ставшего дозвуковым, происходит в криволинейном расширяющемся канале (нас торможение дозвукового потока сейчас не интересует).

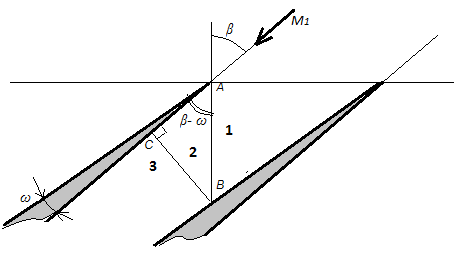
Рис.11. Компрессорная решётка из клиньев. К задаче 5.4

Газ, подлежащий сжатию – воздух (k=1.4), число Маха на входе в решётку М₁. Найти оптимальное значение угла клина решётки ω, обеспечивающее минимальные потери в скачках уплотнения. Для определения угла скачка β воспользоваться диаграммой, приведённой на рис.12. 

 

 

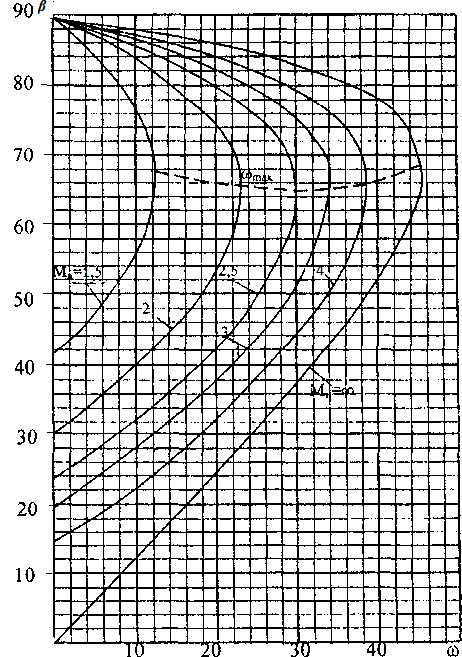
Рис.12. Диаграмма косых скачков. К задаче 5.4

 

Смысл задачи следующий: перед сжатием воздушного потока в компрессоре воздух сначала нужно затормозить. Очевидно, наилучшим вариантом было бы осуществить изоэнтропийное торможение, тогда потери энергии были бы наименьшими из всех возможных. Однако, реальный существенно сверхзвуковой поток в реальных стенках, если на входе в компрессор вообще не ставить решётку, будет тормозиться посредством ударных волн с криволинейным фронтом, что повлечёт большие потери энергии.

Ставя на входе решётку из клиньев, мы принудительно заставляем поток тормозить через косой и прямой скачки, ожидая, что в этом случае суммарные потери энергии будут меньше. Задавая разные углы клиньев, получим разные потери энергии. Если угол клина совсем  мал, очевидно, косой скачок будет очень слабым, поток после него останется сверхзвуковым, и затем произойдёт довольно сильный прямой скачок. Суммарные потери энергии сложатся из малой величины на косом скачке и большой на прямом. Если угол клина сделать несколько больше, потери энергии на косом скачке увеличатся, а на прямом – уменьшатся. Если угол клина сделать ещё больше, может возникнуть ситуация, когда косой скачок сразу переведёт поток в дозвуковой режим. Тогда замыкающего прямого скачка не будет,  все потери энергии – это потери на косом скачке. Наша задача – найти значение угла клина, обеспечивающего с минимальные потери энергии на скачках. При этом, очевидно, проверять нужно значения ω< ω_пред(М₁), поскольку в противном случае косой скачок сойдёт с носика клина, превратится в отошедшую ударную волну; установка такой решётки не имеет смысла. Например, если число Маха входного потока М₁=1.5, нужно проверять значения угла клина ω≤12^о, поскольку ω_пред(М₁=1.5)≈12.3^о (см.рис.12), а для М₁=2 проверять нужно углы клина ω≤23^о.

 

Изобразим процесс торможения потока в hs-диаграмме (рис.13). Исходное состояние потока – точка 1. В этом состоянии поток обладает сверхзвуковой скоростью и удельной кинетической энергией w₁²/2, некоторым значением удельной энтропии s₁, давлением р₁. Изоэнтропийное торможение потока изображается движением вверх по вертикали s₁=const . Поднявшись по исходной изоэнтропе до точки 0, мы получим энтальпию торможения h ₀ = c_p ∙ T ₀, характеризующую запас энергии потока. Энтальпия торможения и температура торможения сохраняются, даже если поток проходит через скачки уплотнения; h ₀ = const, Т₀= const.

На скачках уплотнения (и косых, и прямых) происходит скачкообразное уменьшение скорости, рост температуры, плотности и давления. Скачок – необратимое явление; согласно 2-му началу термодинамики, энтропия на скачке должна увеличиваться. Переход через косой скачок изображается смещением вправо (рост энтропии) и вверх (уменьшение скорости). Получаем точку 2 – состояние потока после косого скачка. Линия перехода через скачок изображена пунктиром, поскольку изображать в равновесных термодинамических диаграммах неравновесные процессы можно лишь условно. Если течение осталось сверхзвуковым, как показано на рис. 13, далее происходит прямой скачок – опять движемся вправо и вверх, получаем точку 3; w₃<w_*  - поток стал дозвуковым. На hs-диаграмме хорошо видно, что после каждого скачка уменьшается давление торможения (а значит, и плотность торможения): если подняться вверх по изоэнтропам s₂= const.  и s₃= const.  до пересечения с изоэнтальпой h ₀ = const и провести через точки 0’и 0” изобары 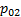  и 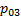, окажется, что изобара  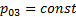расположена ниже изобары 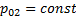, а та, в свою очередь, ниже изобары 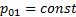, следовательно, .

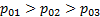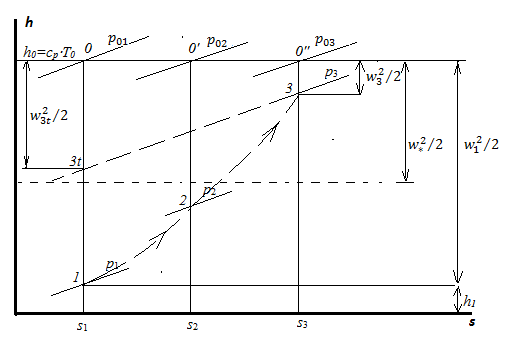
Рис.13. hs-диаграмма к задаче 5.4

Для решения задачи прежде всего нужно  ввести величину, которая бы характеризовала потери энергии. Введём КПД компрессорной решётки η. Обычно КПД устройства определяется как отношение двух величин, имеющих смысл энергии, работы или теплоты. В данном случае речь идёт о потерях кинетической энергии при торможении потока. На входе поток имел удельную кинетическую энергию 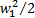, давление p ₁, после двух скачков стало: энергия 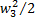, давление p ₃. Потери кинетической энергии составили:

.

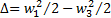       С чем корректно сравнить эту величину? Очевидно, с потерями энергии при изоэнтропийном торможении от исходного давления p ₁ до конечного p ₃. Если продлить изобару p ₃ = const до пересечения с исходной изоэнтропой s ₁ = const, получим точку 3 t с удельной кинетической энергией потока 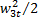. Обычно точка 3 t находится вблизи критической точки, т.е. скорость  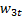чуть меньше или чуть больше критической скорости. Потери энергии при изоэнтропийном торможении составят .

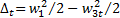       С учётом изложенного выше, КПД решётки:

.

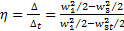Поскольку критическая скорость определяется температурой торможения (формула (4.5)), то из условия Т₀= const следует постоянство критической скорости. Поделив числитель и знаменатель на постоянную величину - критическую энергию, получим более удобную форму выражения КПД компрессорной решётки:

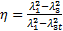 .                                    (a)

Чем выше КПД, тем ближе потери в неизоэнтропийном торможении со скачками к минимально возможному значению – потерям в изоэнтропийном торможении. Таким образом, следует искать такое значение угла клина, при котором КПД максимален:

.

 

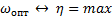Решение задачи

Задав значение числа Маха М₁=1.5 (варианты 1…11) или М₁=2 (варианты 12…30), в табл.14, ответ будем искать совместными усилиями нескольких студентов, каждый из которых должен выполнить свою часть работы, определив КПД при заданном значении угла клина ω. При решении используем таблицу газодинамических функций из задачи (4.1). Можно пользоваться и формулами, но таблица существенно упрощает решение, хотя и несколько снижает точность.

1). По М₁ из таблицы находим значения λ₁, π₁ и q₁.

Затем для заданного угла клина ω из диаграммы (рис.12) определяем угол скачка β, выбирая меньшее значение.

2). Чтобы найти λ₃, сначала необходимо определить λ₂. Для этого запишем условие равенства касательных составляющих скорости на косом скачке (см. рис.9):

;

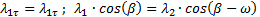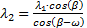                             (b)

3). Если 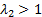, вслед за косым скачком происходит прямой, связь параметров «2» и «3» определяется формулой Прандтля:

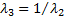 .                           (c)

Если же 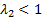, то прямого скачка не будет, поток после косого скачка уже дозвуковой; принимаем:

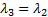.                                (d)

На hs- диаграмме это означает слияние изоэнтроп s₂= const и s₃= const, точек 2 и 3.

4). Определив по (c) или (d) 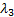, по таблице находим π₃ и q₃.

5). Осталось найти .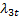

Выделим струйку тока поперечным сечением  S₁, проходящую через косой скачок. Как видно из рис.9, после перехода через фронт скачка поток не только уменьшает скорость и поворачивается на угол ω, но и прижимается к поверхности клина: S₂< S₁. Связь площадей до и после скачка легко найти из подобия треугольников:

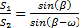.                       (e)

Теперь запишем условие сохранения массового расхода в точках (1), (2), (3), используя форму (4.23):

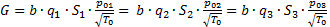.      (f)

 Важно помнить, что температура торможения не меняется, а давление торможения – меняется. Кроме того, используем связь площадей на косом скачке (e) и учтём, что на прямом скачке площадь поперечного сечения с двух сторон от линии скачка одинакова: S₂= S₃.

Из (f) получаем:         ,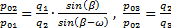

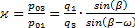.                             (g)

Величину ϰ  называют коэффициентомнеизоэнтропийности; он показывает, насколько велики потери энергии за счёт необратимости процесса (насколько правее от исходной изоэнтропы

s ₁ = const находится конечная изоэнтропа, в данном случае s ₃ = const).

Далее рассуждаем так: скоростному коэффициенту 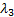 соответствует безразмерное давление 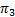, которое мы нашли из таблицы. При этом  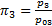- результат деления давления в точке (3) на давление торможения той изоэнтропы, на которой находится точка (3).

По той же логике скоростному коэффициенту 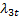 соответствует безразмерное давление  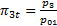– размерное давление в точках (3) и (3 t) одинаково, но точка (3 t) лежит на исходной изоэнтропе s ₁ = const, давление торможения которой р₀₁.

Как легко заметить, между давлениям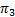и  и 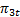 есть связь:

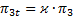.                                     (h)

Таким образом, после определения параметров «3» мы находим коэффициент неизоэнтропийности ϰ по (g), затем безразмерное давление 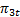 по (h), и по таблице находим .

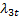6). Определив все необходимые скоростные коэффициенты, подставляем их в (а) и находим КПД решётки для заданного угла клина.

                                              Таблица 14

№	M1	ω,0	№	M1	ω,0	№	M1	ω,0
1	1.5	2	11	1.5	12	21	2	14
2	1.5	3	12	2	2	22	2	15
3	1.5	4	13	2	4	23	2	16
4	1.5	5	14	2	6	24	2	17
5	1.5	6	15	2	8	25	2	18
6	1.5	7	16	2	9	26	2	19
7	1.5	8	17	2	10	27	2	20
8	1.5	9	18	2	11	28	2	21
9	1.5	10	19	2	12	29	2	22
10	1.5	11	20	2	13	30	2	23

 

 

Сопло Лаваля

При адиабатическом течении идеального газа по каналу переменного сечения изменение скорости потока в канале определяется изменением площади поперечного сечения канала согласно уравнению Гюгонио. Это уравнение уже было приведено в разделе 4, формула (4.19).

Приведём уравнение Гюгонио ещё раз:

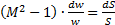 .                      (6.1)

Дозвуковой поток разгоняется в суживающемся канале (рис.14а):

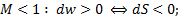            (6.2а)

замедляется в расширяющемся канале:

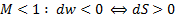.            (6.2б)

Сверхзвуковой поток разгоняется в расширяющемся канале (рис.14б):

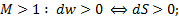            (6.3а)

замедляется в суживающемся канале:

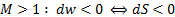.            (6.3б)

Что касается поведения звукового потока, из уравнения Гюгонио нельзя определить знак 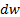, но можно утверждать, раз левая часть уравнения равна нулю, то и правая часть должна быть равна нулю: 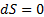, т.е. критическое сечение, если оно существует в потоке, совпадает с экстремумом площади, и очевидно, что этот экстремум – минимум.

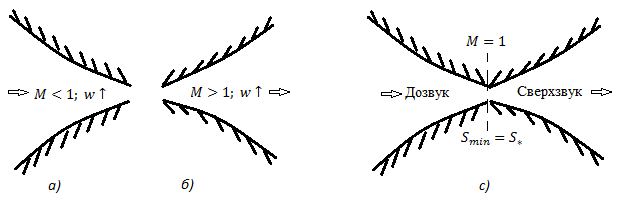
Рис.14. Построение сопла Лаваля

       Из этих рассуждений вытекает идея построения сопла, состоящего из двух частей (рис.14с): входная часть – суживающаяся, в которое подаётся дозвуковой поток газа (входная скорость может быть любой из диапазона 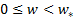). Часто считают, что газовый поток во входном сечении практически заторможен, что соответствует истечению из большого бака через малое отверстие.

       В тот момент, когда разгоняющийся поток достигнет скорости звука, т.е. будет 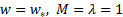, нужно прекратить уменьшать площадь сечения сопла, и начать её увеличивать – присоединить вторую, расширяющуюся часть сопла. Тогда, при благоприятном сочетании входного и выходного давлений, будет осуществлён плавный разгон потока от дозвукового режима на входе через скорость звука в минимальном сечении (его ещё называют горлом сопла) к сверхзвуку на выходе из сопла.

       Впервые подобная конструкция была предложена в 1890 г.  шведским изобретателем и промышленником Карлом Густафом Патриком де Лавалем (1845-1913) для паровых турбин; впоследствии сопло получило имя в честь изобретателя – сопло Лаваля.

Сопло Лаваля применяется в турбинах, в сверхзвуковых реактивных авиационных двигателях, в ракетных двигателях.

Сопло Лаваля можно использовать не только для разгона, но и для охлаждения потока газа или пара, в том числе и для ожижения потока (см. изоэнтропийные формулы).

 

Однако, не всегда в сопле Лаваля можно осуществить переход к сверхзвуку – расчётный режим работы.

Рассмотрим, какие режимы течения могут реализовываться в сопле Лаваля в зависимости от соотношения входного и выходного давлений.

На рис.15 сверху изображена половина профиля сопла (обычно сопла имеют симметричную конструкцию). Форма первой, входной части – фигурная, с криволинейными образующими; о расчёте профиля этой части сопла будет сказано далее. Образующие второй, выходной части - прямые, т.е. расширяющаяся часть представляет собой усечённый круглый конус; угол раствора расширяющейся части α обычно весьма мал, чтобы предотвратить отрыв потока от стенок. Обозначим входное сечение «1», выходное «2».

Будем изображать изменение давления и скоростного коэффициента по длине сопла. Для анализа выбраны именно эти  параметры, поскольку графики изменения температуры и плотности выглядят, с точностью до масштабных множителей, как график давления, а график размерной скорости и числа Маха – как график λ.

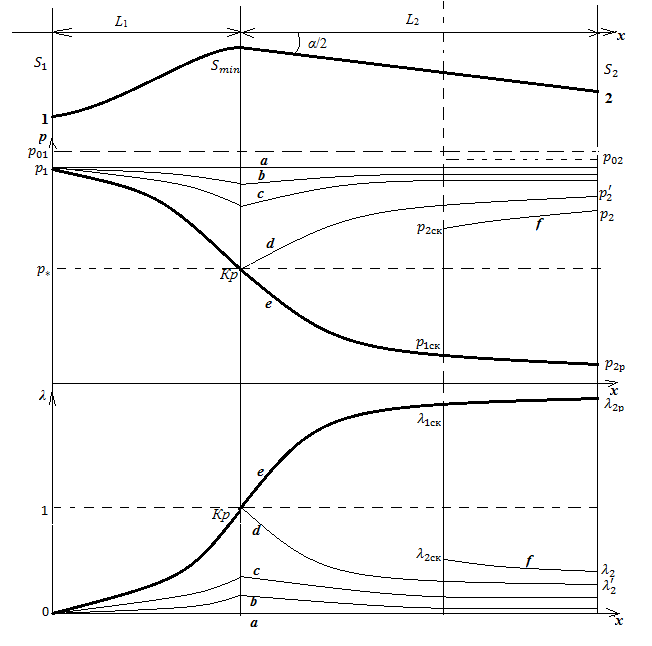
Рис.15. Режимы работы сопла Лаваля

Если входное и выходное давление одинаковы, 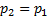то никакой причины потоку двигаться вдоль сопла нет;  давление по длине сопла постоянно, скорость равна нулю (рис.15, линия a). Немного снизим противодавление 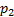, т.е. создадим малый перепад давлений на сопло 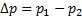. Газ при этом начнёт с небольшой, гарантированно дозвуковой скоростью двигаться вдоль сопла. В суживающейся части сопла  поток будет ускоряться по (6.2а), а давление, следовательно,  уменьшаться. Выйдя в расширяющуюся часть сопла, поток, оставшийся дозвуковым,  будет замедляться (6.2б), давление же начнёт расти. Этот режим, целиком дозвуковой, на рис.15 обозначен линией b.

Еще немного уменьшим выходное давление. Уровень скоростей во всей проточной части сопла повысится, а уровень давления снизится. Поскольку поток во всей области течения дозвуковой, давление в суживающейся части сопла, как и на предыдущем режиме, уменьшается, а в расширяющейся части – увеличивается. Минимальное давление (максимальную скорость) поток по-прежнему имеет в минимальном сечении (в горле) сопла (линия с).

Снижая далее противодавление р₂, при некоторой величине 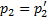 получим режим, в котором давление в горле сопла достигнет критического значения 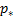. При этом число Маха окажется равным единице, и минимальное сечение сопла станет критическим. Однако в расширяющейся части сопла Лаваля поток останется дозвуковым, поскольку 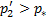. Очевидно, рост давления во второй части сопла возможен только при уменьшении скорости. Таким образом, и в этом режиме (линия d) минимальное давление (критическое) и максимальная скорость (звуковая) поток имеет в горле.

Важно, что в режиме с противодавлением 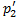 происходит запирание сопла Лаваля, т.к. критическое сечение перестает пропускать вверх по потоку (ко входу) распространяющиеся со скоростью звука возмущения со стороны выходного сечения. При дальнейшем снижении противодавления все параметры потока, включая давление и скорость, в суживающейся части сопла Лаваля перестают меняться (жирная линия от входного сечения до критики на рис. 15). Перестанет меняться и расход газа, достигнув при  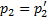максимума. В дозвуковых адиабатных течениях невязкого газа не возникают явления, вызывающие рост энтропии. Поэтому все рассмотренные выше режимы работы сопла Лаваля – изоэнтропийные.

В hs- диаграмме (рис.16) режимы  b , c , d  изображались бы движением вниз (разгон в первой части сопла), затем вверх (торможение во второй части сопла) по исходной изоэнтропе s ₁. При этом в первых двух режимах перемещения по изоэнтропе происходят выше критической точки; в режиме d – сначала спуск до критической точки, потом подъём вверх до точки 2’.

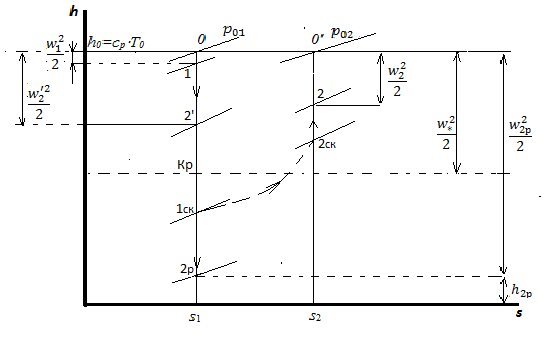
Рис.16. hs- диаграмма режимов течения в сопле Лаваля

Иначе обстоит дело на режимах с противодавлением меньшим, чем 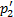. Уже при небольшом снижении p₂ относительно  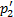непосредственно за критическим сечением в расширяющейся части сопла Лаваля потока становится сверхзвуковым, и согласно (6.3а) во второй части сопла скорость должна непрерывно увеличиваться, а давление, следовательно,  непрерывно падать вплоть до выходного сечения  (рис. 15, линия e). Режим e называется расчётным; он соответствует непрерывному разгону потока от дозвуковой скорости на входе через звуковой режим в горле к сверхзвуку на выходе. Давление, температура, плотность так же непрерывно уменьшаются от входа к выходу. Расчётному режиму течения соответствует противодавление 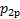, скорость на выходе .

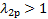В энтальпийно-энтропийной диаграмме расчётный режим изображается непрерывным движением вниз по изоэнтропе s ₁; точка 2р располагается ниже критической.

 

Но что будет, если противодавление p₂ выше давления расчётного режима, т.е. 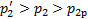? Чтобы давление на выходе из сопла стало равным заданному значению p₂, в некотором сечении потока снижение давления должно смениться его ростом, а увеличение скорости – её уменьшением. В изоэнтропийном течении, согласно уравнению Гюгонио, это невозможно. Но даже в идеальном газе возможны неизоэнтропийные явления – скачки уплотнения. Если в расширяющейся части сопла Лаваля произойдёт прямой скачок уплотнения, сверхзвуковая скорость потока скачкообразно сменится дозвуковой (режим f на рис.15). Пройдя прямой скачок уплотнения, поток становится дозвуковым, скорость его в расширяющемся канале уменьшается по (5.2б), а давление, скачком увеличившееся на скачке, продолжает возрастать далее до выходного сечения.

       В hs-диаграмме в режиме с прямым скачком уплотнения сначала движемся вниз по изоэнтропе s ₁ до точки 1ск. Эта точка находится ниже критической (поток уже стал сверхзвуковым), но выше 2р. Скачок изображается пунктирной линией вправо (рост энтропии) и вверх (уменьшение скорости). После скачка течение вновь становится изоэнтропийным, но теперь мы находимся на изоэнтропе s ₂, s ₂> s ₁. Точка 2ск расположена выше критической, поскольку после прямого скачка поток стал дозвуковым. Дальнейшее торможение потока изображается движением вверх по изоэнтропе s ₂ до точки 2.

 

Местоположение прямого скачка уплотнения определяется величиной p₂. Чем ниже противодавление p₂, тем ближе к выходному сечению он располагается. При некотором противодавлении 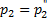 скачок уплотнения достигает выходного сечения. Дальнейшее снижение противодавления вызывает распад прямого скачка уплотнения на систему косых, а при некоторых режимах – и криволинейных скачков уплотнения, расчет которых в рамках одномерного подхода выполнить невозможно. С приближением противодавления к расчетному значению  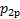интенсивность скачков уплотнения снижается, и течение на расчетном режиме становится изоэнтропийным. При снижении противодавления в зоне  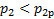за пределами выходного сечения сопла образуется сложная система скачков уплотнения, также не подающаяся одномерному расчету. Таким образом, среди режимов адиабатного сверхзвукового течения в сопле Лаваля изоэнтропийным оказывается лишь расчетный режим.

 

---

Дата добавления: 2021-12-10; просмотров: 108; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!