Характеристики одноканальной СМО

С неоднородной нагрузкой.

Рассмотрим характеристики функционирования ОК СМО с неоднородной нагрузкой. Пусть в СМО поступают заявки Н классов с параметрами:

– l₁, l₂, ... , l_н — интенсивность поступления;

– n_а₁, n_а₂, ... , n_а_н — КВ интервалов поступления;

– b₁, b₂, ... , b_н — среднее время обслуживания;

– n₁, n₂, ... , n_н — КВ длительности обслуживания.

Приведенные параметры полностью описывают систему, которая является СМО типа

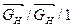Характеристики СМО в случае неоднородной нагрузки определяются как для заявок отдельных классов, так и для заявок объединенного потока, и те и другие характеристики во многом аналогичны соответствующим характеристикам системы с однородной нагрузкой.

Характеристики заявок отдельных классов.

1) Pr{n₁, n₂, ..., n _H} — вероятности состояний СМО, где под состоянием системы здесь понимается вектор 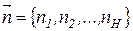, показывающий, сколько заявок каждого класса находятся в системе.

2) r_к=l_к b_к — загрузка СМО заявками класса k (k–заявок). При этом, загрузка r_к имеет тот же физический смысл, что и в случае однородной нагрузки, но только применительно к классу k .

3) w_k — среднее время ожидания k–заявок.

4) u_k=w_k+b_k — среднее время пребывания в системе k–заявок.

5) l_k=l_kw_k — средняя длина очереди заявок класса k.

6) m_k=l_k u_k =l_k+r_k — среднее число k–заявок в системе .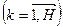

Соотношения взаимосвязи между характеристиками заявок отдельных классов такие же, что и в случае однородной нагрузки. Эти соотношения также всегда справедливы, если только СМО является системой без отказов.

Характеристики заявок объединенного потока.

1) 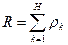— суммарная загрузка системы и СМО функционирует в стационарном режиме, если R<1. При этом h=1–R — коэффициент простоя.

2) 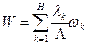— среднее время ожидания заявок объединенного потока, где 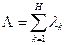— интенсивность результирующего потока.

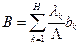3) — среднее время пребывания, где — усредненное время обслуживания.

4) 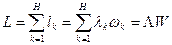— средняя (суммарная) длина очереди.

5) — среднее число заявок в системе.

Характеристики многоканальной СМО

(однородная нагрузка).

Рассмотрим МК СМО из N обслуживающих приборов, в которую поступает поток заявок интенсивности l и КВ n_а интервалов поступления. Все приборы совершенно идентичны и среднее время обслуживания в одном приборе равно b, а КВ длительности обслуживания – n. Определим для описанной МК СМО (типа G/G/N)характеристики функционирования.

1) Вероятности состояний. Под состоянием МК СМО как и в случае ОК СМО понимается число заявок k, находящихся в системе, и вероятность такого состояния также обозначается через P_k_, k = 0, 1, 2, ...

2) Загрузка. По аналогии с ОК СМО произведение lb можно было бы трактовать как загрузку МК СМО. Однако это не так и в качестве загрузки МК СМО принимается загрузка ее одного прибора, определяемая как r= lb/N. Это делается с тем, чтобы использовать одинаковые обозначения для загрузки, придать одинаковый смысл загрузке, "приравнять" отдельные приборы МК СМО и прибор в ОК СМО. После такого определения загрузки МК СМО для нее справедливы все утверждения, приведенные ранее относительно загрузки ОК СМО. Отношение l/ N=l¢ в выражении для загрузки характеризует интенсивность заявок, приходящих на один прибор МК СМО. Условием существования стационарного режима: r=l¢b<1.

3) Среднее число заявок m в МК СМО определяется так же, как и в ОК:

m= .

4) Средняя длина очереди

l= ,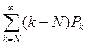

где k– N — число заявок в очереди, когда в системе находится k заявок.

5) Среднее время ожидания w определяется по формуле Литтла:

w=l/l.

6) Среднее время пребывания

u=m/l=w+b.

7) Вероятность ожидания или вероятность того, что все N приборов заняты обслуживанием заявок

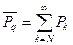8) Для МК СМО представляет интерес такая характеристика как среднее число 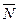занятых приборов, определяемая следующим равенством:

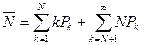С другой стороны, 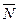— это среднее число заявок, находящиеся в обслуживающих приборах, т.к., очевидно, что число занятых приборов всегда равно числу заявок в приборах. Вспомним, что загрузка r=lb/ N — это среднее число заявок в приборе (одном). Тогда среднее число заявок в N приборах равно Nr. Таким образом

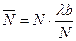=lb.

Очевидно, что m=l+ 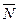(сравните с m=l+r для ОК СМО). Действительно

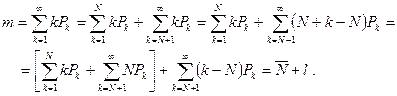
Вывод формулы Литтла.

Универсальная формула Литтла (справедлива для любой системы без отказов) устанавливает связь между средними значениями числа заявок, времени пребывания и интенсивности поступления. Так для СМО в целом эта связь имеет вид: m=lu, вывод которой приводится ниже.

Рассмотрим производную СМО и достаточно длинный интервал (0, t) ее функционирования. Пусть a(t) — число заявок, поступивших в систему, а d(t) — число заявок, покинувших ее за время t.

Очевидно, что n(t)=a(t)–d(t) — число заявок в системе в момент времени t. С другой стороны, площадь между кривыми a(t) и d(t) (заштрихованная площадь) на интервале (0, t) есть общее (суммарное) время, проведенное всеми заявками в системе на момент времени t. Обозначим это общее время через g(t).

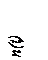Пусть l_t — интенсивность поступления заявок в систему на интервале (0, t). Очевидно, что l_t=

Пусть u_t — среднее время пребывания заявок в системе на интервале (0, t). Тогда u_t = .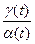

Пусть m_t — среднее число заявок в системе на интервале (0, t). Тогда m_t= 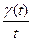. Из полученных равенств имеем:

Пусть существуют пределы l= 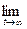l_t, u= 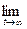u_t и m= 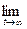m_t_,что имеет место, если система имеет стационарный режим функционирования. Тогда m=ll, что и требовалось показать.

Теперь если под "системой", о которой шла речь выше, понимать "очередь" или "прибор", то получим соответствующие выражения для средней длины очереди (l=lw) и среднего числа заявок в обслуживающем приборе (r=lb).

Дата добавления: 2021-12-10; просмотров: 21; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!