А) Производная от неопределённого интеграла равна подынтегральной функции
Действительно, по определению неопределённого интеграла:
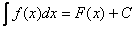, следовательно:
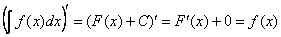, что и требовалось доказать.
Б) Дифференциал от неопределённого интеграла равен подынтегральному выражению
Действительно , по правилу раскрытия дифференциала и только что доказанному пункту:
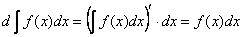
2 ) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной :
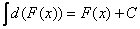
Учитывая, что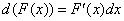 
, свойство можно переписать в следующем виде:
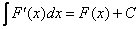
Действительно, поскольку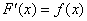 
то получается непосредственно само определение неопределённого интеграла.
Отметим , в обоих случаях значки дифференциала и интеграла взаимно уничтожаются, что естественно, так как действия интегрирования и дифференцирования взаимообратны.
Константу можно вынести из-под знака интеграла
То есть, если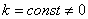 
, то 
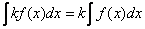
Доказательство:
Найдём производную левой части. Используем свойство №1:
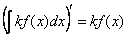
Найдём производную правой части. Используем правило дифференцирования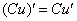 
и свойство №1:
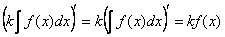
Получены одинаковые результаты, из чего и следует справедливость данного свойства.
4) Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов :
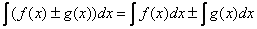
Справедливо для любого количества слагаемых.
Свойство проверяется точно так же, как и предыдущее – берутся производные от обеих частей
Таблица неопределенных интегралов
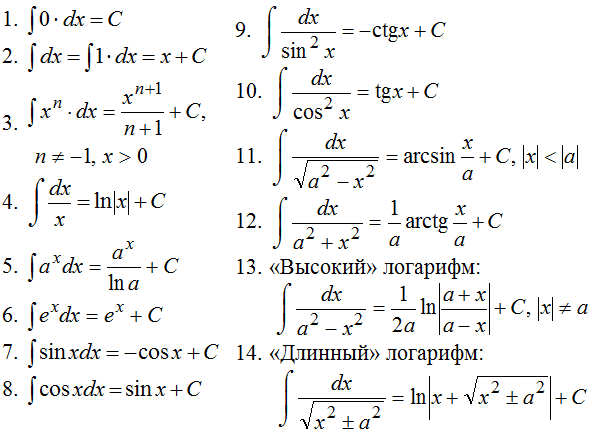
Первые 12 формул выучить наизусть (при а=1) !!!
Примеры нахождения неопределенного интеграла
Найти интеграл – это значит найти определенную функцию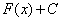 
, пользуясь некоторыми правилами, приемами и таблицей .
например, табличный интеграл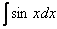 
равен функции 
.
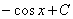Так как дифференцирование и интегрирование – противоположные действия, то для любой первообразной, которая найдена правильно, справедливо следующее :
Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.
Вернемся к тому же табличному интегралу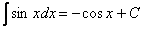 
.
Найти неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию.
Например, решением интеграла 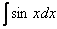являются функции 
, 
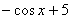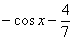, и т. д.
Решений бесконечно много, поэтому записывают коротко: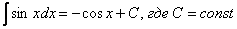 
При нахождении неопределенного интеграла пользуются
свойствами линейности неопределенного интеграла:
1) – постоянный множитель можно (и нужно) вынести за знак интеграла.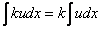 
2) – интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности.
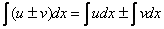
Данное свойство справедливо для любого количества слагаемых.
Пример 1
Найти неопределенный интеграл. Выполнить проверку.
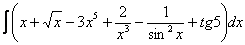
Решение:
(1) Применяем правило .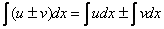
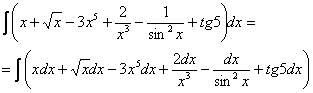
(2) Согласно правилу 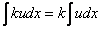, выносим все константы за знаки интегралов. Учитывая , что в последнем слагаемом 
– это константа, её также выносим.
(3) Все интегралы табличные, поэтому, используем табличные формулы
, 
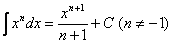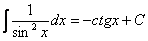и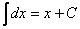 
.
Замечания
1. Формулу интегрирования степенной функции встречается наиболее часто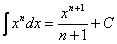 
, ее надо помнить.
2. Следует отметить, что табличный интеграл 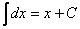– частный случай формулы интегрирования степенной функции
.
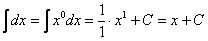3. Константу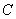 
достаточно поставить один раз в конце выражения (а не ставить их после каждого интеграла) .
(4) Записываем полученный результат в более компактном виде, все степени вида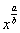 
снова представляем в виде корней, степени с отрицательным показателем – сбрасываем обратно в знаменатель.
Проверка.
Для того чтобы выполнить проверку нужно продифференцировать полученный ответ:
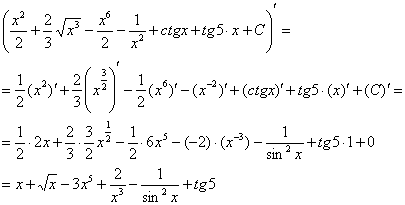
Получена исходная подынтегральная функция, значит, интеграл найден правильно.
Пример 2 -самостоятельно
Найти неопределенный интеграл. Выполнить проверку.
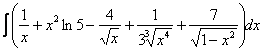
Пример 3
Найти неопределенный интеграл. Выполнить проверку.
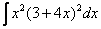
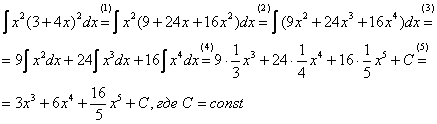
(1) Используем формулу квадрата суммы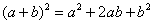 
, избавляясь от степени.
(2) Вносим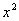 
в скобку, избавляясь от произведения.
(3) Используем свойства линейности интеграла (оба правила сразу).
(4) Превращаем интегралы по табличной формуле .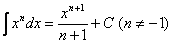
Проверка:
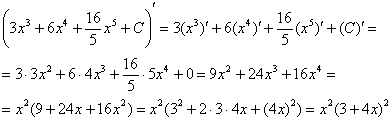
Получена исходная подынтегральная функция, значит, интеграл найден правильно
Пример 4
Найти неопределенный интеграл. Выполнить проверку.
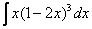
Это пример для самостоятельного решения.
Пример 5
Найти неопределенный интеграл. Выполнить проверку.
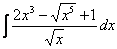
В данном примере подынтегральная функция представляет собой дробь. Когда мы видим в подынтегральном выражении дробь, то первой мыслью должен быть вопрос: А нельзя ли как-нибудь от этой дроби избавиться, или хотя бы её упростить?
Замечаем, что в знаменателе находится корень из «икс». Можно почленно разделить числитель на знаменатель:
Пример 6
Найти неопределенный интеграл. Выполнить проверку.
Это пример для самостоятельного решения.
Дата добавления: 2021-12-10; просмотров: 28; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!