Свойства неопределённого интеграла
Лекция. Первообразная и неопределенный интеграл
Понятие первообразной и неопределенного интеграла
Свойства неопределённого интеграла
Таблица неопределенных интегралов
Примеры нахождения неопределенного интеграла
Понятие первообразной и неопределенного интеграла
К понятию первообразной функции приводят многие задачи экономики.
Общая же постановка вопроса такова: имеется некоторая функция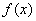 
и нужно выяснить, производную от какой функции она представляет . То есть, необходимо найти такую функцию 
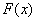, чтобы выполнялось равенство:
.
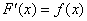Определение:
функция 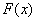называется первообразной для функции 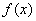на некотором промежутке, если для всех 
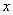из этого промежутка выполняется равенство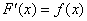
Например, для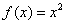 
первообразной функцией на всей числовой прямой будет являться функция 
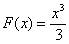. И действительно, для любого «икс»:
.
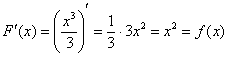Теорема
Пусть 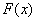– какая-нибудь первообразная для функции 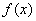на некотором промежутке.
Тогда функция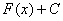 
, где 
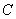– произвольная константа, тоже будет первообразной функцией для 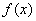на данном промежутке.
Доказательство:
поскольку производная константы равна нулю, то:
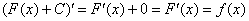, следовательно, 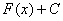– первообразная для функции 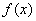по определению первообразной, что и требовалось доказать.
Так, для функции 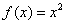первообразной будет являться любая функция из множества 
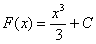, где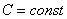 
(вместо С можно подставлять конкретные числовые значения).
|
|
|
Докажем обратное утверждение: любая другая первообразная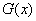 
для функции 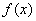отличается от 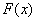лишь на константу, иными словами:
.
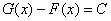В предыдущем примере можно поставить вопрос – вдруг для функции 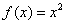существует не только 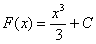, а какая-нибудь ещё первообразная?
Предположим , что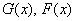 
– это две первообразные для функции 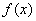на некотором промежутке. Тогда для любого «икс» из данного промежутка производная разности будет равна:
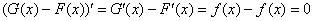, или если записать короче:
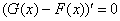
Но с другой стороны, известно, что данному условию удовлетворяет функция-константа и только она:
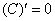
Откуда и следует равенство 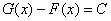, которое требовалось доказать. Таким образом, любая первообразная для функции 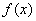имеет вид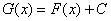 
Определение:
Множество всех первообразных 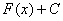для функции 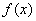называется неопределённым интегралом от функции 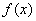и обозначается символом 
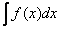. Таким образом, по определению:
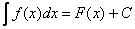, где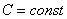
Функция 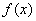называется подынтегральной функцией, 
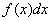– подынтегральным выражением, а сам процесс отыскания множества первообразных 
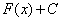– интегрированием.
Интегрирование – это обратное действие по отношению к дифференцированию (восстановление функции 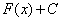по её производной )
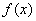Для нашего примера:
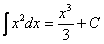, где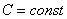
Проверка: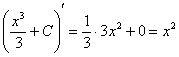 
– исходная подынтегральная функция.
|
|
|
Встает вопрос :любая ли функция интегрируема? Оказывается, нет.
Сформулируем достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.
То есть , для существования первообразной достаточно лишь непрерывности функции .
Свойства неопределённого интеграла
1) Производная от неопределённого интеграла равна подынтегральной функции, а дифференциал от неопределённого интеграла равен подынтегральному выражению :
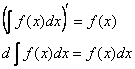
Доказательство:
Дата добавления: 2021-12-10; просмотров: 17; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!