Метод Мак-Класски (алгебраический метод)
Алгебраический метод известен как метод Мак-Класски, модифицировавшего в 1956 году метод Квайна. Базируется данный метод на следующей теореме.
Теорема. 3.1.Если в СДНФ функции алгебры логики произвести всевозможные операции неполного склеивания, а затем всевозможные операции элементарного поглощения, то полученная форма функции будет сокращенной.
Элементарную конъюнкцию ранга n будем называть min-термом ранга n.
Элементарная конъюнкция 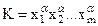 называется импликантой булевой функции
называется импликантой булевой функции  , если
, если 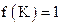 , то есть булева функция на данном наборе является константной и равна 1.
, то есть булева функция на данном наборе является константной и равна 1.
Этот метод является модернизацией метода Квайна (его 1-го этапа). Мак-Класски предложил записывать исходные импликанты данной функции, заданной в СДНФ, в виде их двоичных кодов (каждому члену ставится в соответствие по известному правилу его собственная вершина). Все множество так записанных импликант разбивается по числу единиц в их кодах на группы (в i -ую группу войдут коды, имеющие в своей записи i единиц). Попарное сравнение импликант достаточно производить только между соседними группами, т.к. только эти группы отличаются одним знаком в кодах входящих в них членов. Сравнивая коды членов соседних групп, образуют члены низшего ранга. На месте исключенного знака пишут в них «тире». Затем всю совокупность членов низшего ранга снова разбивают на группы по местоположению знака «тире». Снова сравнивают члены, но уже внутри групп, образуя члены низшего ранга по тому же правилу и т.д. Далее все производится по методу Квайна, но в кодовых значениях импликант.
|
|
|
Сформулируем алгоритм метода Мак-Класски.
1 этап. Разделить двоичные векторы области единиц логической функции на секции в соответствии с их индексами. Индекс двоичного вектора это число единиц, входящих в состав этого вектора. Составить таблицу интервалов, используя правило склеивания. Склеивать между собой только те двоичные векторы, которые отличаются друг от друга только в одной координате (ближайшие векторы). Склеивание происходит по этой координате. Ближайшие векторы могут находиться только в соседних секциях таблицы. В конце первого этапа получают все простые импликанты логической функции.
2 этап.В ходе второго этапа полученное множество простых импликант минимизируют, т.е. выбирают минимальное количество простых импликант, которое позволяет покрыть всю область единиц логической функции (типичная задача нахождения оптимального покрытия).
Пример.Задана булева функция f (X1, X2, X3, Х4)=Σ(0,2,5,6,7,8,9,14,15)
Найти МДНФ методом Мак-Класски.
Решение: Выпишем двоичные векторы области единиц логической функции и найдем их индексы
|
|
|
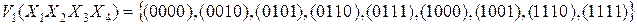
0 1 2 2 3 1 2 3 4
1 этап. Нахождение всех простых импликат логической функции.
Разделим двоичные векторы на секции в соответствии с их индексами и получим таблицу интервалов.
| Индекс | Интервал |
| 0 | 0000 |
| 1 | 0010 |
| 1000 | |
| 2 | 0101 |
| 0110 | |
| 1001 | |
| 3 | 0111 |
| 1110 | |
| 4 | 1111 |
Склеиваем между собой ближайшие векторы соседних секций пока это возможно.
| Индекс | Интервал | Интервал | Интервал | |||
| 0 | 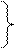 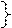 0000 0000
| 0-1 | 00-0 A1 -000 A2 | 2-3-3-4 | -11- A6 -11- | |
| 1 |
| |||||
| 1-2 | 0-10 A3 100- A4 | |||||
| 2 |
1001 | |||||
| 2-3 | 01-1 A5
| |||||
| 3 | 0111 1110 | |||||
| 3-4 | -111 111- | |||||
| 4 | 1111 |
Все оставшиеся не склеенными интервалы образуют множество простыхимпликат логической функции. Простые импликаты обозначаем А1...А6.
2 этап. Минимизация полученного множества простыхимпликат логической функции.
«*» – вектор в данный простой импликат.
| Implikant | 0000 0 | 0010 2 | 0101 5 | 0110 6 | 0111 7 | 1000 8 | 1001 9 | 1110 14 | 1111 15 |
| A1 00-0 | * | * | |||||||
 A2-000 A2-000
| * | * | |||||||
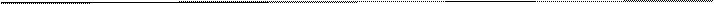 A30-10 A30-10
| * | * | |||||||
| A4 100- | * | * | |||||||
| A5 01-1 | * | * | |||||||
| A6 -11- | * | * | * | * |
|
|
|
Все векторы области единицдолжны быть покрыты простыми импликантами (в каждом столбце должен быть хотя бы один «*»), и импликант должно остаться минимальное количество.
Оптимальное покрытие в данном случае: А1, А4, А5, А6.
МДНФ: 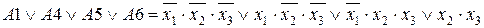 .
.
Дата добавления: 2021-12-10; просмотров: 70; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 0010
0010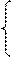 1000
1000 0101
0101
 0110
0110 011-
011- -110
-110