МинимизацияФАЛ методом равносильных преобразований
Лекция 3. Минимизация функций алгебры логики
План лекции:
Основные понятия
МинимизацияФАЛ методом равносильных преобразований
Метод неопределенных коэффициентов
Многомерный куб
Карты Карно
Метод Квайна
Метод Мак-Класски (алгебраический метод)
Основные понятия
Любая ФАЛ может быть записана в виде СДНФ или СКНФ. Покажем на примере, что такая запись в ряде случаев является неэкономной.
Пример. Пусть ФАЛ задана в СДНФ.
f(x1, x2, x3)= 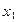 &x2&x3
&x2&x3 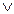 x1& x2&
x1& x2& 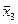
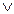 x1&
x1& 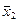 & x3
& x3 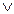 x1&
x1& 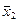 &
& 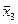
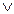
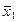 & x2& x3.
& x2& x3.
Добавим к функции один конъюнктивный член 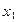 &x2&x3. Это добавление не меняет данной функции, так как x
&x2&x3. Это добавление не меняет данной функции, так как x 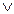 x = x :
x = x :
f(x1, x2, x3)= 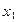 x2x3
x2x3 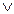 x1 x2
x1 x2 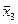
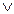 x1
x1 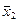 x3
x3 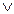 x1
x1 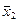
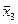
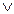
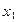 x2x3
x2x3 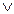
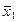 x2x3.
x2x3.
Преобразуем это выражение, используя сочетательные и распределительные свойства конъюнкции и дизъюнкции:
f(x1, x2, x3)= 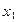 x2 (x3
x2 (x3 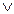
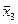 )
) 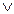 x1
x1 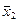 ( x3
( x3 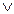
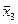 )
) 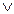 x2 x3 (x1
x2 x3 (x1 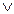
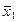 ).
).
Используя свойство дизъюнкции, 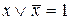 получаем:
получаем: 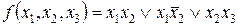
Аналогично предыдущему делаем дальнейшие преобразования:
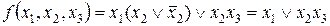 .
.
Из примера виднанеэкономность совершенных нормальных форм для представления ФАЛ.
Проблема простейшего представления функций сводится к проблеме выбора базиса и проблеме наиболее экономного представления функций в этом базисе.
К настоящему времени существенные результаты в решении задачи минимизации лишь в базисе, состоящем из отрицания, конъюнкции и дизъюнкции.
Приведем ряд определений.
Определение. Конъюнкция 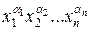 называется элементарной, если в этой конъюнкции каждая переменная встречается не более одного раза.
называется элементарной, если в этой конъюнкции каждая переменная встречается не более одного раза.
Определение. Ранг элементарной конъюнкции – это число элементов, образующих эту конъюнкцию. Ранг – это ''n''.
Определение. Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).
Определение. ДНФ для функции f(x 1 , x 2 ,…, xn), состоящей из элементарных конъюнкций ранга n, называется дизъюнктивной совершенной нормальной формой.
Из этого определения следует, что в СДНФ входят конъюнкции наибольшего возможного для данной функции ранга.
Определение.Длиной ДНФ называют число элементарных конъюнкций, образующих эту ДНФ.
Определение.ДНФ, имеющая наименьшую длину по сравнению со всеми другими ДНФ, эквивалентными данной функции, называют кратчайшей ДНФ.
Определение.ДНФ, содержащая наименьшее число букв 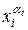 по сравнению со всеми другими ДНФ, эквивалентными данной функции, называется минимальной ДНФ.
по сравнению со всеми другими ДНФ, эквивалентными данной функции, называется минимальной ДНФ.
Аналогичные определения можно дать для случая конъюнктивных нормальных форм.
Дизъюнктивная (конъюнктивная) нормальная форма – это дизъюнкция (конъюнкция) конечного числа различных членов, каждый из которых представляет собой конъюнкцию (дизъюнкцию) отдельных переменных или их отрицаний, входящих в данный член не более одного раза.
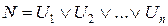 , где
, где
U 1,…Un — элементарные конъюнкции.
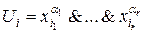 ,
,
где все 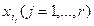 различны; число r– ранг конъюнкции.
различны; число r– ранг конъюнкции.
Известно, что любая булева функция, отличная от нуля, может быть представлена совершенной ДНФ.f(x 1 ,…, xn)= 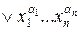 ,
, 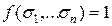
Совершенная ДНФ есть частный случай ДНФ.
Члены Д(К)НФ, представляющие собой элементарные конъюнкции (дизъюнкции) k букв, называют минитермами (макстермами) k ранга.
Если исходная формула содержит другие операции, то они предварительно выражаются через &, V, ù, например,
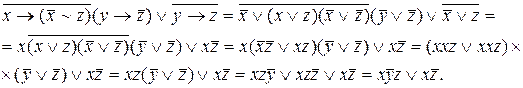
Определение.Импликантом функции f(x 1 ,…, xn) называется элементарная конъюнкция 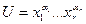 если выполнено соотношение
если выполнено соотношение 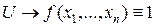 ,где
,где 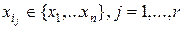 .
.
Пример. Элементарная конъюнкция 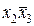 являетсяимпликантойфункции
являетсяимпликантойфункции 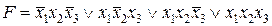 .
.
Очевидно, любая элементарная конъюнкция произвольной ДНФ, представляющей функции f(x 1 ,…, xn), является ее импликантом, так как если эта элементарная конъюнкция на некотором наборе обращается в единицу, то функция f(x 1 ,…, xn) тоже обращается в единицу.
Определение. Простым импликантомf(x 1 ,…, xn) называют импликантf(x 1 ,…, xn), если элементарная конъюнкция, получающаяся из него удалением любой буквы, не является импликантом функции.
Пример. 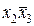 –простаяимпликантабулевой функции
–простаяимпликантабулевой функции 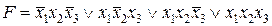 , а импликанта
, а импликанта 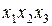 не является простой для этой функции, так как
не является простой для этой функции, так как 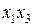 (собственная часть импликанты
(собственная часть импликанты 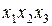 ) является импликантой функции F .
) является импликантой функции F .
Определение. Сокращенной ДНФ (СкДНФ) функции f(x 1 ,…, xn) называется дизъюнкция всех простых импликантов функции f(x 1 ,…, xn).
Пример. 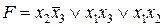 являетсяСкДНФ булевойфункции
являетсяСкДНФ булевойфункции 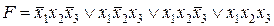 . Отметим, что СкДНФ является единственной для конкретной булевой функции F .
. Отметим, что СкДНФ является единственной для конкретной булевой функции F .
Определение. ДНФ булевой функции F, содержащая наименьшее число слагаемых среди всех ДНФ, реализующих функцию F, называется кратчайшей ДНФ (КрДНФ).
Пример. 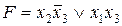 –КрДНФэтой же булевой функции
–КрДНФэтой же булевой функции 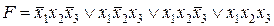 .
.
Вообще говоря, для заданной булевой функции F существует несколько различных по числу вхождений литералов КрДНФ.
Определение.Минимальная ДНФ f(x 1 ,…, xn) получается из сокращенной ДНФ f(x 1 ,…, xn) удалением некоторых элементарных конъюнкций.
Отметим, что для заданной булевой функции F существует, вообще говоря, несколько МДНФ, отличающихся друг от друга числом слагаемых.
Более того, МДНФ не всегда совпадает с КрДНФ булевой функции n переменных F . Хотя для начальных значений n (n=2 или n=3) МДНФ всегда совпадает с КрДНФ.)
Пример. 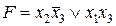 является КрДНФ и МДНФ рассматриваемой функции
является КрДНФ и МДНФ рассматриваемой функции 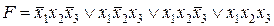 .
.
Определение. Тупиковой ДНФ f(x 1 ,…, xn) называется дизъюнкция простыхимпликантов, из которых ни один простой импликант нельзя удалить так, чтобы полученная ДНФ все еще представляла функцию.
Легко понять, что любая минимальная ДНФ является тупиковой, а обратное не верно.
Получение минимальной ДНФ можно осуществить в два этапа. На первом этапе находят сокращенную ДНФ. На втором этапе строят тупиковые ДНФ функции, удаляя подмножества элементарных конъюнкций из сокращенной ДНФ. Из полученных тупиковых ДНФ выбирают минимальные.
Рассмотрим первый этап получения сокращенной ДНФ. Именно, укажем метод получения сокращенной ДНФ функции f(x 1 ,…, xn) из СДНФ функции f(x 1 ,…, xn) последовательным применением к ней двух равносильных преобразований:
1. Операции полного склеивания, которая состоит в замене выражения 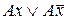 на А.
на А.
2. 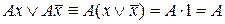 – операции неполного склеивания, которая состоит в замене выражения
– операции неполного склеивания, которая состоит в замене выражения 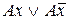 на
на 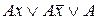 , так как
, так как 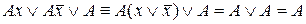 .
.
3. Операции поглощения, которая состоит в замене выражения 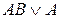 на
на 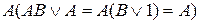 ,гдеА и В – произвольно элементарные конъюнкции.
,гдеА и В – произвольно элементарные конъюнкции.
В общем случае процесс построения минимальных ДНФ может быть охарактеризован следующей схемой
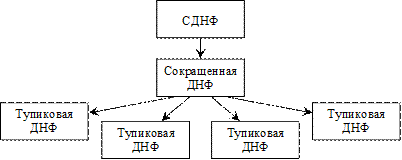
МинимизацияФАЛ методом равносильных преобразований
Любая булева функция представима в СН(Д или К) формах. Более того, такое представление является первым шагом перехода от табличного задания функций к ее аналитическому выражению.
В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получаются на основе принципа двойственности.
Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний).
Такие формы называют минимальными.
Формула, представленная в ДНФ, упрощается многократным применением операции склеивания 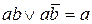 и операций поглощения
и операций поглощения 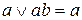 и
и 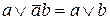 (дуальные тождества для конъюнктивной нормальной формы имеют вид:
(дуальные тождества для конъюнктивной нормальной формы имеют вид:
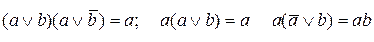 ).
).
Здесь под а и b можно понимать любую форму булевой алгебры.
В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются невозможными, т.е. получаем тупиковую форму.
Среди тупиковых форм находится и минимальная ДНФ, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма – минимальная, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.
Пример. Составить по таблице истинности СДНФ булевой функции 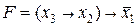 и минимизировать ее, применяя законы склеивания.
и минимизировать ее, применяя законы склеивания.
Решение.
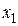
| 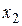
| 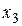
| 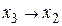
| 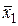
| 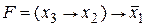
|
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
СДНФ будет иметь вид: 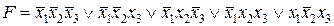 .
.
Минимизируем ее, применяя законы склеивания. Подчеркнем конъюнкции, которые можно склеить. Очевидно, что это можно сделать различными способами, например:
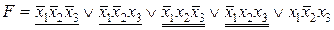 ,
,
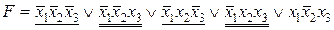 ,
,
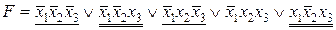 ,
,
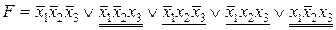 .
.
Выберем один из возможных вариантов склеивания, например 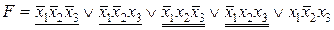 и минимизируем ДНФ:
и минимизируем ДНФ:
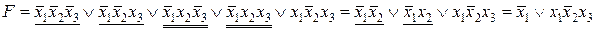 .
.
Замечание.При минимизации ДНФ достаточно часто (но не всегда!) удается получить лучшие результаты, если «нарастить» данную ДНФ используя свойство идемпотентности дизъюнкции: 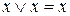 .
.
Например, в рассматриваемом примере пятую, последнюю конъюнкцию 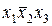 можно было бы склеить со второй конъюнкцией
можно было бы склеить со второй конъюнкцией 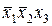 . Добавив вторую конъюнкцию еще раз, мы не изменим саму булеву функцию, но получим в результате минимизации ДНФ более короткое ее представление:
. Добавив вторую конъюнкцию еще раз, мы не изменим саму булеву функцию, но получим в результате минимизации ДНФ более короткое ее представление:
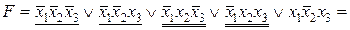
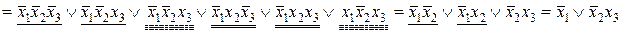 .
.
Работа на таком уровне подобна блужданию. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать графические и аналитические представления.
Пример. Составить СДНФ булевой функции, заданной вектором значений таблицы истинности w(F)=(10010010) и минимизировать ее, применяя законы склеивания.
Решение.Так как вектор значений заданной булевой функции имеет 8=23 разрядов, следовательно, булевой функции соответствует следующая таблица истинности:
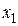
| 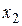
| 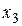
| F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
СДНФ будет иметь вид: 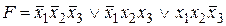 .
.
Минимизировать данную функцию, применяя законы склеивания, невозможно.
Дата добавления: 2021-12-10; просмотров: 29; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
