Определение устойчивости САР по критерию Гурвица
Чтобы определить устойчивость САР по критерию Гурвица, необходимо вначале найти характеристическое уравнение замкнутой САР.
Передаточная функция разомкнутой системы получена выше:
Для замкнутой системы в случае единичной отрицательной обратной связи передаточная функция будет равна:
,
где знаменатель, приравненный к нулю, есть характеристическое уравнение для замкнутой САР, т.е.:
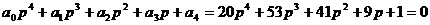
Определитель Гурвица составляется следующим образом. Все коэффициенты от а1 до а4 располагаются по главной диагонали в порядке возрастания индексов.
Вверх от главной диагонали в столбцах записываются коэффициенты характеристического уравнения с последовательно возрастающими, а вниз — с убывающими индексами. На месте коэффициентов, индексы которых больше 4, и меньше чем нуль, проставляются нули. Составляем определитель из коэффициентов характеристического уравнения:
Находим величины 2-го и предпоследнего (в нашем случае 3-го) определителей Гурвица
По критерию Гурвица система устойчива только тогда, когда все коэффициенты аi характеристического уравнения и все определители Гурвица Dп до n-1 порядка, где n-наибольшая степень характеристического уравнения, больше нуля.
Вывод.Так как определитель Гурвица Dn положительны, то согласно критерию Гурвица рассматриваемая САР устойчива.
Определение устойчивости САР по критерию Михайлова
|
|
|
Рассмотрим пример исследования замкнутой системы автоматического регулирования на устойчивость по критерию Михайлова.
Пусть имеется характеристический полином (знаменатель передаточной функции замкнутой САР) вида
.
Заменяем в этом полиноме оператор p на jω и выделяем действительную и мнимую части полученного выражения:
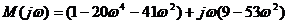
Теперь, задавая значения частоты ω от нуля до бесконечности в рад/с, находим значения действительной и мнимой частей вектора Михайлова М(jω), а затем по ним стоим годограф Михайлова (рисунок 3).
| ω | 0 | … | 
| 0,04 | … | ∞ |
| Re(ω) | 1 | … | 0 | -8,8 | … | ∞ |
| Im(ω) | 0 | … | -135,8 | 0 | … | -∞ |
Таблицу можно формировать так, чтобы находить только точки пересечения годографа Михайлова с действительной Re(ω) и мнимой Im(ω) осями комплексной плоскости.
Рисунок 5 - Годограф Михайлова, построенный для исследуемой САР
Вывод: Поскольку мы исследуем САР четвертого порядка и годограф Михайлова начал свое движение с положительной действительной оси (значение Re(0)=1), прошел против часовой стрелки три квадранта комплексной плоскости, нигде не петляя и не обратившись в нуль, а в третьем квадранте устремился в бесконечность, то замкнутая САР устойчива.
|
|
|
5. 
Разработка схем автоматического управления производственными процессами.
Дата добавления: 2018-02-15; просмотров: 622; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!