Механические характеристики двигателей с последовательным возбуждением.
1)
Основное уравнение движения электропривода.
При переменных статических моментах и моментах инерции, зависящих от
скорости, времени, угла поворота вала двигателя (линейного перемещения РО), уравнение движения электропривода записывается в общем виде:
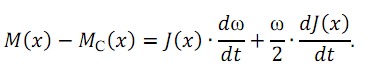
При постоянном моменте инерции 
уравнение упрощается
Его называют основным уравнением движения.
Правую часть уравнения 
называют динамическим
моментом. Знак 
определяет знак производной 
и состояние
электропривода:
– двигатель разгоняется;
- двигатель снижает скорость;
– установившийся режим работы двигателя, его скорость неизменна.
Темп разгона зависит от момента инерции ܬ электропривода, определяющего
способность механической части электропривода запасать кинетическую
энергию
Для анализа режимов работы и решения задач удобнее записать основное
уравнение движения в относительных единицах (о.е.). Приняв за базовые
значения момента Мб=Мн – номинальный электромагнитный момент двигателя, скорости ωб=ωон – скорость идеального холостого хода при номинальном напряжении на якоре и номинальном токе возбуждения, основное уравнение движения в о.е. записывается в виде
где механическая постоянная времени электропривода, учитывающая и приведенный момент инерции РО. Наличие в уравнении 
свидетельствует о записи уравнения в о.е. Для расчета и построения нагрузочных диаграмм М(t)и ω(t) используется
|
|
|
решение основного уравнения движения
из которого для конечных приращений при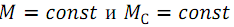 
для заданного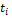 
получим приращение скорости
и значение скорости в конце участка 
2)
3)
Характеристики ДПТ с независимым возбуждением.
Характерной особенностью таких двигателей является независимость тока возбуждения (или потока возбуждения) от тока якоря машины. Разновидностью независимого возбуждения является возбуждение от постоянных магнитов.
Механические характеристики ДПТ с независимым возбуждением:
С учётом того, что
и 
или 
основное уравнение ДПТ в двигательном режиме работы
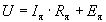
можно привести к виду
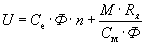
Разрешив последнее уравнение относительно n, получим уравнение механической характеристики ДПТ с независимым возбуждением в виде
или
,
где 
- скорость идеального холостого хода машины,
-изменение скорости, обусловленное моментом нагрузки двигателя.
Сама механическая характеристика ДПТ с независимым возбуждением приведена на рис.6.6 и представляет собой прямую линию, наклон которой к оси абсцисс зависит от величины потока возбуждения и сопротивления якоря Rя. Чем меньше величина потока возбуждения и чем больше сопротивление Rя, тем круче механическая характеристика.
|
|
|
Как следует из уравнения механической характеристики, скорость двигателя при постоянном моменте нагрузки можно регулировать тремя способами:
1.Изменением напряжения на якоре двигателя,
2.Изменением сопротивления в цепи якоря двигателя,
3.Изменением потока возбуждения машины.
При регулировании скорости первым из названных способов, напряжение на якоре изменяется либо с помощью реостата (рис.6.7,а), либо с помощью усилительно –преобразовательного устройства (рис.6.7,б), при этом поток возбуждения остаётся постоянным.
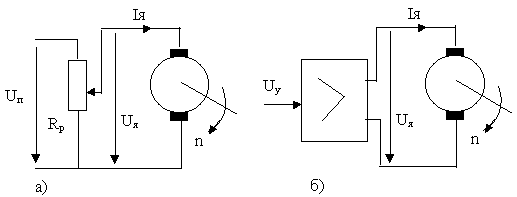
Рис. 6.7, a, б
Семейство механических характеристик, соответствующих данному способу регулирования, приведено на рис.6.8.
Рис. 6.8, а, б
С изменением напряжения U пропорционально изменяется и скорость холостого хода
при этом угол наклона (или жестокость) механических характеристик остаётся неизменной.
4)
Механические характеристики двигателей с последовательным возбуждением.
В ДПТ с последовательным возбуждением поток возбуждения создаётся током якоря машины, для чего обмотка возбуждения и якорь двигателя включаются последовательно относительно источника питания, как показано на схеме рис. 6.13.
|
|
|
Рис. 6.13
Обычно при токах 
магнитная цепь машины не насыщена и поток возбуждения пропорционален току возбуждения
.
При больших токах якоря 
магнитная цепь машины насыщена, и поток возбуждения можно считать постоянным.
Подставив в уравнение 
,
где 
, а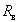 
- сопротивление обмотки возбуждения, значение , получим
.
Зная, что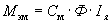 
, получим
,
где 
– постоянные.
Поскольку в установившемся режиме 
, то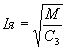 
и уравнение механической характеристики ДПТ с последовательным возбуждением в диапазоне нагрузок принимает вид 
которому соответствует гиперболическая кривая, приведённая на рис. 6.14.
Рис. 6.14
Способность двигателей последовательного возбуждения развивать большой электромагнитный момент, пропорциональный квадрату тока якоря, обеспечивает этим двигателям хорошие пусковые свойства, т. е. большой пусковой момент при сравнительно малом токе якоря. Поэтому такие двигатели применяют в грузоподъёмных и тяговых приводах. Следует обратить внимание на недопустимость работы электродвигателей с последовательным возбуждением в режиме холостого хода или с нагрузкой, менее 25% от номинальной – это приводит к разносу двигателя.
|
|
|
3)4) под вопросом.
Механические и электромеханические характеристики ДПТ.
Важнейшей характеристикой двигателя является механическая n(M). Она показывает, как зависит частота вращения двигателя от развиваемого момента. Если к обмоткам двигателя подведены номинальные напряжения и отсутствуют дополнительные резисторы в его цепях, то двигатель имеет механическую характеристику, называемую естественной. На естественной характеристике находится точка, соответствующая номинальным данным двигателя (Мн, Ря и т.д.). Если же напряжение на обмотке якоря меньше номинального, либо Iв < Iвн, то двигатель будет иметь различные искусственные механические характеристики. На этих характеристиках двигатель работает при пуске, торможении, реверсе и регулировании частоты вращения.
Преобразовав выражение 
относительно частоты вращения где rЯ - сопротивление якоря, получим уравнение электромеханической характеристики n(Iя):
(7)
После замены в уравнении (7) тока Iя согласно формуле 
, где КМ - коэффициент, зависящий от конструктивных параметров машины; Ф - магнитный поток одного полюса; IЯ - ток якоря, получим уравнение механической характеристики n(М):
(8)
При Ф = соnst, электромеханическая n(Iя) и механическая n(М) характеристики двигателя параллельного возбуждения представляют собой прямые линии. Так как за счет реакции якоря магнитный поток немного изменяется, то характеристики в действительности несколько отличаются от прямых.
При работе вхолостую (М = 0) двигатель имеет частоту вращения холостого хода, определяемую первым членом уравнения (8). С увеличением нагрузки n уменьшается. Как следует из уравнения (8), это объясняется наличием сопротивления якоря rя.
Поскольку rя не велико, частота вращения двигателя при увеличении момента изменяется мало, и двигатель имеет жесткую естественную механическую характеристику (рис.4, характеристика 1).
Из уравнения (8) следует, что регулировать частоту вращения при заданной постоянной нагрузке (М = const) можно тремя способами:
а) изменением сопротивления цепи якоря;
б) изменением магнитного потока двигателя;
в) изменением напряжения на зажимах якоря.
4)под вопросом
Дата добавления: 2018-02-15; просмотров: 661; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!