Линейное неоднородное уравнение второго порядка с постоянными коэффициентами
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом: Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a = c и b = d. Суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d). Произведением двух комплексных чисел a + ib и c + id называется комплексное число ac – bd + i(ad + bc).
Алгебраическая форма
Запись комплексного числа z в виде x + iy,  , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.
Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i2 = − 1):
(a + ib) + (c + id) = (a + c) + i(b + d);

Геометрическая интерпретация комплексного числа
Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x и y. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называетсядействительной, а Oy - мнимой.
Расстояние r точки z от нулевой точки, т. е. число
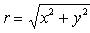

называется модулем комплексного числа z и обозначается символом |z|.
Тригонометрическая и показательная формы
Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент 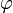 (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме
(x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме
z = r(cos φ + isin φ).
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
z = reiφ,
где eiφ — расширение экспоненты для случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:

6)Извлечение корней из комплексных чисел


7) Дифференциальное уравнение — уравнение, связывающее некоторую функцию с ее производными. Решить дифференциальное уравнение — найти функции, при подстановке которых в уравнение оно обращается в тождество. Большинство физических законов записывается в виде дифференциальных уравнений. Примером дифференциального уравнения является второй закон Ньютона: F = ma
где сила F является функцией координат и времени, ускорение a = v'(t) = x''(t) — производная скорости и вторая производная координаты по времени.
8) Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:

где функции P(t,x) и Q(t,x) определены и непрерывны в некоторой области  .
.
9) 1.2.3. Утверждение об уравнении с разделенными переменными. Пусть в уравнении
| f(x)dx = g(t)dt, | (3) |
функции f и g на своих областях определения имеют первообразные F и G:
| F′(x) = f(x) (x ∈ D(f)), G′(t) = g(t) (t ∈ D(g)). | (4) |
Тогда уравнение (3) эквивалентно уравнению
| F(x) = G(t) + C (x ∈ D1). | (5) |
Другими словами, (5) есть полный интеграл уравнения (3).
Д о к а з а т е л ь с т в о. Пусть область определения D(φ) функции x = φ(t) есть промежуток и φ есть решение уравнения (3). Это означает, что
| [f(x)dx – g(t)dt]|x = φ(t), dx = φ′dt = 0 (t ∈ D(φ), dt ∈ R). |
В силу условий (4) последнее равенство эквивалентно тождеству
| d[F(x) – G(t)]|x = φ(t), dx = φ′dt)] ≡ 0 (t ∈ D(φ), dt ∈ R), |
которое в силу инвариантности формы первого дифференциала, в свою очередь, эквивалентно соотношению
| d[F(φ(t)) – G(t)] = 0 (t ∈ D(φ), φ ∈ D1). |
Наконец, последнее, очевидно эквивалентно тождеству
| F[φ(t)] = G(t) + C (t ∈ D(φ), φ ∈ D1), |
означающему, что φ — решение (5).
Однородные уравнения
Функция 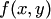 называется однородной функцией своих аргументов измерения
называется однородной функцией своих аргументов измерения 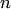 , если справедливо тождество
, если справедливо тождество 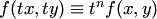 .
.
Например, функция  есть однородная функция второго измерения, так как
есть однородная функция второго измерения, так как

При  имеем функцию нулевого измерения. Например,
имеем функцию нулевого измерения. Например,  есть однородная функция нулевого измерения, так какДифференциальное уравнение вида
есть однородная функция нулевого измерения, так какДифференциальное уравнение вида  называется однородным относительно
называется однородным относительно 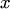 и
и  , если
, если 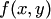 есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде
есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде
 (1)
(1)
Вводя новую искомую функцию 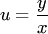 , уравнение (1) можно привести к уравнению с разделяющими переменными:
, уравнение (1) можно привести к уравнению с разделяющими переменными:

Если  есть корень уравнения
есть корень уравнения  , то решение однородного уравнения будет
, то решение однородного уравнения будет  или
или  (прямая, проходящая через начало координат).
(прямая, проходящая через начало координат).
11)Линейные дифференциальные уравнения первого порядка
Определение. Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Пример. Найти общее решение уравнения y'+3y=e2x и частное решение,удовлетворяющее начальным условиям х=0, у=1.
Решение. Данное уравнение является линейным.
Здесь ρ(x)=3 и f(x)=e2x.
Решение ищем в виде y=U∙υ, где U и υ – некоторые функции от х. Находим y'= U'υ+ Uυ' и подставляем в уравнение значениеy и y', получаем: U'υ+Uυ'+3Uυ=e2 x или U'υ+U(υ'+3υ)= e2x.
Найдем одно значение υ, при котором выражение в скобках, обращается в нуль: υ'+3υ=0. Получим уравнение с разделяющимися переменными. Решая его получаем: 
 ln υ =–3x,υ=e–3x.
ln υ =–3x,υ=e–3x.
Подставляем найденное значение υ в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:
 .
.
Итак, общее решение данного уравнения имеет вид: 
12)Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Уравнение вида y''+ρy'+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Рассмотрим линейное уравнение второго порядка вида:
y''+ρy'+qy=0, (1)
у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.
Уравнение
K2+ρK+q=0 (2)
называется характеристическим уравнением данного уравнения (1).
Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.
Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ2–4q уравнения (2) следующим образом:
1. При D>0 корни характеристического уравнения вещественные и различные (К1≠К2), и общее решение имеет вид  .
.
2. При D=0 корни характеристического уравнения вещественные и равные (К1=К2=К), и общее решение имеет вид: 
3. Если D<0, то корни характеристического уравнения комплексные:  , где
, где  – мнимая единица,
– мнимая единица,  и общее решение (К1=α+βi, К2=α–βi, β≠0), имеет вид y=eαx(C1 cosβx+C2 sinβx).
и общее решение (К1=α+βi, К2=α–βi, β≠0), имеет вид y=eαx(C1 cosβx+C2 sinβx).
Линейное неоднородное уравнение второго порядка с постоянными коэффициентами


 Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения
Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения 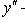

 и некоторого частного решения
и некоторого частного решения 
 неоднородного.
неоднородного.
Дата добавления: 2018-02-18; просмотров: 430; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
