Уравнения в полных дифференциалах. Интегрирующий множитель.
Уравнение
 (1)
(1)
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции  , т.е.
, т.е.
 .
.
Теорема. Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой односвязной области  изменения переменных
изменения переменных 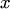 и
и  выполнялось условие
выполнялось условие
 (2)
(2)
Общий интеграл уравнения (1) имеет вид  или
или

ИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
Основные понятия
Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде 
или, если это возможно, в виде, разрешенном относительно старшей производной: 
16) Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Пусть  — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность
— числовая последовательность; рассмотрим наравне с данной последовательностью последовательность

каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида

Вообще, для обозначения ряда используется символ 
поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.
В соответствии с этим говорится о сходимости числового ряда:
|
|
|
§ числовой ряд сходится, если сходится последовательность его частичных сумм;
§ числовой ряд расходится, если расходится последовательность его частичных сумм:
§ числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.
Если числовой ряд сходится, то предел S последовательности его частичных сумм носит название суммы ряда: 
Признаки сходимости и расходимости рядов с неотрицательными членами.
Ряд с неотрицательными членами сходится тогда и только тогда, когда последовательность частичных сумм ограничена сверху.
18)Признак сравнения рядов с положительными членами. Пусть даны два ряда с неотрицательными членами  an и
an и  bn. Если существует натуральное число N такое, что неравенство an ≤ bn выполнено для всех n ≥ N, то из сходимости ряда
bn. Если существует натуральное число N такое, что неравенство an ≤ bn выполнено для всех n ≥ N, то из сходимости ряда  bn следует сходимость ряда
bn следует сходимость ряда  an, а из расходимости ряда
an, а из расходимости ряда  an -расходимость ряда
an -расходимость ряда  bn.
bn.
19) Признак Коши.
а) Если существует натуральное число N такое, что для числовой последовательности {  }, построенной из членов ряда
}, построенной из членов ряда  an, an ≥ 0, для всех n ≥ N выполняется неравенство
an, an ≥ 0, для всех n ≥ N выполняется неравенство  ≤ q < 1 (q — фиксированное число, не зависящее отn), то ряд сходится; если для всех n ≥ N выполняется неравенство
≤ q < 1 (q — фиксированное число, не зависящее отn), то ряд сходится; если для всех n ≥ N выполняется неравенство  ≥ 1, то ряд расходится.
≥ 1, то ряд расходится.
|
|
|
б) Если у последовательности {  }, построенной из членов ряда
}, построенной из членов ряда  an, an ≥ 0, существует
an, an ≥ 0, существует 
 = p, то ряд
= p, то ряд  an сходится при p < 1 и расходится при p > 1.
an сходится при p < 1 и расходится при p > 1.
При p = 1 предельный признак Коши не дает ответа на вопрос, сходится данный ряд или расходится.
19) Интегральный признак (Коши, Маклорен).
Пусть данный ряд имеет вид  an =
an =  f (n), причем f (n) есть значение в точке x = n некоторой функции f (x), определенной при x ≥ n0. Если f (x) монотонно убывает и в области определения справедливо неравенство f (x) ≥ 0, то ряд
f (n), причем f (n) есть значение в точке x = n некоторой функции f (x), определенной при x ≥ n0. Если f (x) монотонно убывает и в области определения справедливо неравенство f (x) ≥ 0, то ряд  an сходится тогда и только тогда, когда сходится несобственный интеграл
an сходится тогда и только тогда, когда сходится несобственный интеграл  f (x) dx.
f (x) dx.
20) Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
 с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство
с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.
21) Признак Даламбера.
а) Если существует натуральное число N такое, что для последовательности чисел qn = , то данный ряд сходится.
21) Признак Даламбера.
а) Если существует натуральное число N такое, что для последовательности чисел qn =  , построенной из членов ряда , построенной из членов ряда  an, an > 0, для всех n ≥ N выполняется неравенство an, an > 0, для всех n ≥ N выполняется неравенство  ≤ q < 1 (q — фиксированное число, не зависящее отn), то ряд сходится; если для всех n ≥ N выполняется неравенство ≤ q < 1 (q — фиксированное число, не зависящее отn), то ряд сходится; если для всех n ≥ N выполняется неравенство  ≥ 1, то ряд ≥ 1, то ряд  an расходится.
б) Если последовательность an расходится.
б) Если последовательность  , построенная из членов ряда , построенная из членов ряда  an, an > 0, имеет некоторый предел n, an, an > 0, имеет некоторый предел n,   =p, то при p < 1 ряд =p, то при p < 1 ряд  an сходится, а при p > 1 расходится (предельный признак Даламбера).
При p = 1 предельный признак Даламбера не дает ответа на вопрос, сходится данный ряд или расходится.
22) Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.: an сходится, а при p > 1 расходится (предельный признак Даламбера).
При p = 1 предельный признак Даламбера не дает ответа на вопрос, сходится данный ряд или расходится.
22) Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:  Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
|
23) Тейлора ряд, степенной ряд вида
|
|
|
 , (1)
, (1)
где f(x) — функция, имеющая при х = а производные всех порядков. Во многих практически важных случаях этот ряд сходится к f(x) на некотором интервале с центром в точке а:
 (2)
(2)
(эта формула опубликована в 1715 Б. Тейлором). Разность Rn(x) = f(x) — Sn(x),где Sn(x) — сумма первых n + 1 членов ряда (1), называется остаточным членом Т. р. Формула (2) справедлива, если  .
.
24) Маклорена ряд, исторически неправильное название (по имени К. Маклорена) степенного ряда вида:
|
|
|
 ,
,
где f(0), f’(0), f”(0), ..., f(n)(0),... – значения заданной функции f(x) и её последовательных производных при х = 0.Этот ряд был получен ранее Маклорена английским математиком Б. Тейлором (опубликовал 1715), что было известно и самому Маклорену. М. р. есть частный случай Тейлора ряда.
Дата добавления: 2018-02-18; просмотров: 685; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 (монотонное невозрастание {an} по абсолютной величине)
1.
(монотонное невозрастание {an} по абсолютной величине)
1. 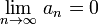 .
Тогда этот ряд сходится.
.
Тогда этот ряд сходится.