Входящий поток и время обслуживания
Методы теории очередей
Возникновение теории телетрафика
В начале XX века стали активно развиваться телефонные сети. Возникли новые задачи планирования этих сетей. Одна из первых задач заключалась в расчете емкости пучка каналов при заданной вероятности потерь. А.К. Эрланг вывел формулу, позволившую решить эту задачу. Данная формула была приведена в девятой лекции. Считается, что именно с работ Эрланга началось развитие теории телетрафика. Единице трафика в 1946 году решением МСЭ было присвоено название "Эрланг".
Первые системы коммутации работали по алгоритму с потерями. Это означает, что при отсутствии свободного обслуживающего прибора заявка теряется. Использование программного управления позволило ввести дисциплину обслуживания с ожиданием. Это увеличило эффективность обслуживания заявок. Широкое применение данного алгоритма обслуживания привело к тому, что вместо словосочетания "Теория телетрафика" стало чаще использоваться название "Теория очередей". В настоящее время "Теория очередей" широко используется для исследования телекоммуникационных сетей, транспортных систем, сферы торговли.
Математический аппарат теории очередей базируется на теории вероятностей. Дело в том, что большинство процессов, свойственных инфокоммуникационным системам, являются случайными. Актуальность теории очередей объясняется рядом факторов, из которых целесообразно выделить следующее утверждение: стоимость телекоммуникационной системы может быть разделена на два слагаемых, зависящих от количества обслуживаемых абонентов и от величины обрабатываемого трафика соответственно.
|
|
|
Классификация
В 1961 году Кендалл (D.G. Kendall) ввел следующее обозначение для систем массового обслуживания: "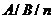 
". Символ " 
" определяет процесс поступления заявок, обозначение " 
" указывает на распределение времени занятия, а величина 
равна числу обслуживающих приборов. Для более полного описания систем телетрафика позже было введено расширенное обозначение Кендалла:
(14.1)
где:
-
– количество мест для ожидания в очереди, -
– число обслуживаемых абонентов, -
– дисциплина обработки заявок.
В первой позиции классификации (14.1) чаще всего стоит символ 
. Это означает, что входящий поток является пуассоновским. Для более сложных моделей используются символы 
(произвольный рекуррентный закон) и 
(произвольный закон с возможной корреляцией).
Во второй позиции обычно используется один из следующих символов: (экспоненциальное распределение), 
(постоянное время обслуживания), 
(распределение Эрланга 
порядка) (произвольный закон распределения). Реже встречаются другие символы.
|
|
|
Классификация алгоритмов обслуживания была приведена в Приложении 1 к девятой лекции. Обычно используются такие дисциплины:
- FCFS: first come – first served (первым пришел – первым обслужен),
- LCFS: last come – first served (последним пришел – первым обслужен),
- SIRO: service in random order (обслуживание в случайной порядке),
- SJF: shortest job first (обслуживание, начиная с "коротких" заявок).
В некоторых случаях вводятся приоритеты. Существует принципиальное различие между двумя видами приоритетов: без прерывания и с прерыванием обслуживаемого требования (non-preemptive and preemptive). Для первой дисциплины поступившая заявка ждет окончания обслуживания менее приоритетного требования. Она будет обслужена сразу после окончания обработки менее приоритетной заявки. При использовании второй дисциплины обслуживание заявки с низшим уровнем приоритета прерывается. Обычно выделяют три способа обслуживания прерванной заявки:
- дообслуживание с момента приостановки менее приоритетного требования,
- обслуживание прерванной заявки заново,
· потеря прерванной заявки.
|
|
|
Входящий поток и время обслуживания
В редких случаях поток заявок можно считать детерминированным. Тогда время между поступлением соседних заявок – постоянная величина. Процесс поступления заявок обычно является случайным. Функция распределения интервалов времени между моментами поступления соседних заявок обозначается как 
. Длительность обслуживания заявок в большинстве случаев также будет случайной величиной с функцией распределения 
. Иногда длительность обслуживания заявок постоянна. Как правило, функциям и свойственна ненулевая дисперсия.
Этот факт иллюстрируют результаты измерений трафика, которые проводятся Операторами ТФОП. На рисунке 14.1 приведены статистические данные о вызовах, которые обслуживаются телефонной станцией. Во всех случаях соединения были установлены для междугородной или международной телефонной связи.
Рис. 14.1. Среднее число вызовов, поступающих в АТС за одну минуту
Гистограмма, показанная на рисунке 14.1, была получена в результате обработки статистических данных, которые собирались в течение десяти дней. Эти десять дней соответствовали двум рабочим неделям. Такая выборка не позволяет судить об изменении количества поступающих вызовов в течение квартала или года. Более того, в некоторых случаях можно выделить тренды, описывающие изменения исследуемого процесса в течение нескольких лет. Тем не менее, данные, подобные тем, что приведены на рисунке 14.1, представляют большой практический интерес.
|
|
|
Статистические данные о числе вызовов собирались за каждую минуту в течение суток. Количество поступивших вызовов усреднялось по интервалам длительностью 15 минут. Такая длительность интервала очень часто используется при измерении трафика в телефонных сетях.
Для большинства систем время обслуживания заявок представляет собой случайную величину. Следовательно, полная информация о длительности обслуживания заявок может быть представлена функцией распределения . Будем считать, что эта функция имеет преобразование Лапласа-Стилтьеса 
. На рисунке 14.2 приведены статистические данные о времени телефонного разговора. Речь идет о среднем значении исследуемой величины.
Рис. 14.2. Среднее время занятия
Среди тех распределений , которые представляют практический интерес, можно выделить семь законов.
Во многих исследованиях, касающихся различных систем, используется гипотеза об экспоненциальном распределении времени обслуживания заявок:
(14.2)
Экспоненциальное распределение существенно упрощает исследование систем телетрафика. Кроме того, многие распределения, более реальные с практической точки зрения, имеют коэффициент вариации менее единицы. Это означает, что результаты, полученные для экспоненциального распределения, позволяют оценить характеристики исследуемой системы "сверху" – для пессимистического сценария. Тем не менее, для многих ситуаций гипотезу об экспоненциальном распределении длительности обслуживания заявок следует считать очень грубым приближением. Это утверждение справедливо и для многих других законов распределения с модой в точке 
.
Распределения с коэффициентом вариации менее единицы часто представимы с помощью распределения Эрланга 
порядка:
. (14.3)
При 
распределение Эрланга вырождается. Этот случай рассматривается как самостоятельное распределение – постоянная длительность обслуживания, равная 
. Для ряда технических систем СМО с постоянным временем обслуживания хорошо описывает процессы функционирования. Функцию проще записать через преобразование Лапласа-Стилтьеса:
. (14.4)
Распределения с коэффициентом вариации более единицы можно представить с помощью гиперэкспоненциального закона. На практике чаще всего используют простейшую форму гиперэкспоненциального распределения:
· длительность обслуживания заявок подчиняется экспоненциальному закону с интенсивностью 
с вероятностью 
;
· длительность обслуживания заявок подчиняется экспоненциальному закону с интенсивностью 
с вероятностью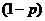 
;
Эти предположения позволяют представить ФР длительности обслуживания в таком виде:
. (14.5)
Комбинация эрланговского и гиперэкспоненциального распределения позволяет хорошо аппроксимировать множество непрерывных функций. Соответствующая функция распределения может быть определена так:
. (14.6)
Для коэффициентов 
должны выполняться два условия:
, 
(14.7)
Следующее распределение – равномерное на отрезке времени 
. Выражение для функции распределения записывается в следующем виде:
. (14.8)
Последнее распределение относится к дискретным. Речь идет о ступенчатой функции, для которой справедливо такой преобразование Лапласа-Стилтьеса:
. (14.9)
Если вид функции распределения времени обслуживания заявок не установлен, то во второй позиции классификации Кендалла используется символ " ". Он свидетельствует о произвольном характере соответствующего распределения.
Для уточнения термина "трафик" рассмотрим рисунок 14.3. Он иллюстрирует изменение числа занятых линий в пучке соединительных линий в течение пяти периодов времени 
. Функция 
, которая принимает положительные целочисленные значения, определяет число занятых линий в момент времени 
. Для каждого периода можно определить среднее значение числа занятых линий. Эта величина может быть дробной.
Рис. 14.3. Число занятых линий за пять отрезков времени
Дата добавления: 2018-02-15; просмотров: 1002; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!