Математические методы оптимизации

Методы анализа и синтеза структуры сети

Задачи анализа и синтеза структуры сетей

Структура сети электросвязи определяет значительную часть важнейших характеристик инфокоммуникационной системы. По этой причине задачи анализа и синтеза структуры сети электросвязи образуют самостоятельное направление среди прикладных исследований, проводимых в интересах всех участников инфокоммуникационного рынка. Безусловно, анализ и синтез структуры сети электросвязи нельзя полностью отделить от других процессов создания и развития инфокоммуникационной системы. Тем не менее, для изучения сложного объекта или процесса необходимо выделить в нем ряд самостоятельных задач.

Задачи анализа и синтеза структуры сети электросвязи объединяются общностью конечных целей, методологическим подходом и математическим аппаратом. Конечная цель этих задач – построение эффективной инфокоммуникационной системы, которая обеспечивает выполнение установленных функций и способна развиваться. Слово "эффективная" указывает на тот факт, что структура сети близка к оптимальной. Методологический подход к анализу и синтезу структуры сети электросвязи можно считать общим в силу универсальности и неразрывности возникающих задач. Математический аппарат, используемый для решения возникающих задач, идентичен.

Задачи анализа структуры, как правило, решаются для эксплуатируемой сети электросвязи. Цель анализа обычно состоит в выявлении "узких мест", свойственных сети, в разработке предложений по развитию сети (качественному и количественному), в оценке ее стоимости при продаже бизнеса. В каждом из этих трех случаев используется разный подход. Тем не менее, математический аппарат анализа структуры сети остается неизменным.

Задачи синтеза структуры сети электросвязи предшествуют процессу создания или радикальной модернизации инфокоммуникационной системы. Для этих двух случаев используемый математический аппарат может различаться весьма существенно. Структура большинства сетей уже создана. Поэтому задачи модернизации инфокоммуникационной системы представляются в настоящее время более актуальными.

Для задач анализа и синтеза структуры сети электросвязи следует учитывать три важных фактора, которые сформировались в последние годы. Эти факторы оказывают существенное влияние на постановку и решение многих важных задач.

Во-первых, большинство сетей начали формироваться очень давно. Их структура, определяемая многими внешними (например, принципы градостроения) и внутренними (например, стоимость отдельных компонентов сети) факторами, не всегда близка к оптимальной. Математические методы оптимизации подробнее рассматриваются в следующем разделе настоящей лекции. Здесь необходимо выделить такой аспект: точная оптимизация некой функции , поведение которой прогнозируется с весьма низкой достоверностью, невозможна.

Во-вторых, новые технологии оказывают очень существенное влияние на принципы построения сетей. Поэтому представление структуры сети в виде графа и проведение соответствующих операций с такой моделью чревато значительными ошибками. Физическая природа технологий требует ее учета при анализе и синтезе современной инфокоммуникационной системы.

В-третьих, представление функций стоимости отдельных компонентов сети при помощи монотонно возрастающих или убывающих кривых (данная практика используется в течение многих лет) часто приводит к большим погрешностям. Такой подход был разработан до широкого распространения вычислительной техники. В настоящее время он должен быть пересмотрен для получения более точных результатов.

Математические методы оптимизации

Оптимизация – как раздел математики – существует не одно столетие. Практическая цель оптимизации заключается в выборе одного варианта из нескольких возможных вариантов или в уточнении какого-либо решения.

Прикладные задачи оптимизации, как правило, очень сложны. Современные методы оптимизации не всегда справляются с решением реальных задач без помощи человека. Не существует такой теории, которая способна учесть любые особенности исследуемого объекта или процесса за исключением очень простых случаев. Телекоммуникационная сеть считается одной из самых сложных систем, созданных руками человека. Поэтому простые задачи встречаются в этой области знаний крайне редко.

Однако для решения практически важных задач необходимы численные оценки – даже весьма приближенные. При этом необходимо понять если не величину ошибки, то хотя бы ее порядок. В ряде случаев допустимы значительные ошибки. Это обусловлено характеристиками используемых технических средств. Например, в начале XX века для организации линии связи между двумя коммутационными станциями использовались многопарные кабели. Было важно точнее оценить число пар, которое, в значительной мере, определяло стоимость проекта. Допустимая ошибка измерялась единицами процентов. В начале XXI века для организации линии связи между двумя коммутационными станциями применяются кабели с оптическими волокнами. Задача состоит в выборе типа системы передачи, величины пропускной способности которых образуют числовой ряд. Каждый член этого ряда предыдущему, умноженному на четыре. Это означает, что допустимая ошибка в расчете необходимого числа каналов измеряется не процентами, а разами.

Для сетей связи общего пользования, как правило, минимизируется стоимостный показатель (обычно – капитальные затраты). При этом технические показатели и атрибуты сети играют роль ограничений. Если удается выразить зависимость стоимости сети в виде функции одной переменной , то задача получения оптимального решения достаточно проста. Обычно задается область изменения аргумента .

Наиболее известный метод оптимизации для функции одной переменной заключается в нахождении ее производной. Если в точке производная равна нулю, то в этой точке имеет минимум или максимум. Максимум достигается при условии, что . В противном случае (когда ) исследуемая функция имеет минимум. При говорят, что функция при имеет стационарное значение. Точка называется стационарной.

Более общее условие формулируется в следующей форме: если существует производная , отличная от нуля, и если , то функция имеет в точке

максимум при четном и ,
минимум при нечетном и . (13.1)

Выражение (13.1) определяет достаточные условия экстремума.

Для нахождения экстремумов функции в области необходимо сначала найти ее производную:

. (13.2)

Это уравнение имеет корни: . К этим корням надо присоединить граничные точки. В результате получается такой ряд:

. (13.3)

Можно убедиться в следующем: в точке наблюдается граничный минимум, а в точке – граничный максимум. Точка определяет локальный максимум функции , а точка – локальный минимум. Для нулевого значения аргумента . Это означает, что точка определяет место перегиба функции .

К сожалению, записать функцию стоимости в виде известной функции не всегда возможно. Тем не менее, ее значения в области определения на отрезке можно получить в виде отсчетов в точках . Для этого отрезок разбивается на равных частей, позволяющих элементарно вычислить :

. (13.4)

Из значений необходимо выбрать экстремум (минимум или максимум). Точность локализации экстремума при использовании полного перебора всех возможных решений определяется величиной :

. (13.5)

Достоинства данного метода – простота. Он может использоваться для функций любого вида, в том числе, имеющих разрывы. Очевидный недостаток этого метода заключается в большом объеме вычислений при необходимости добиться высокой точности результата. Иногда приходится варьировать аргументов исследуемой функции. Тогда вычисления следует провести для числа точек, количество которых равно .

В подобных ситуациях эффективны методы направленного случайного поиска. Их эффективность возрастает, если функция относится к классу унимодальных, то есть на отрезке имеет либо один минимум, либо один максимум. Такое условие справедливо для большинства задач оптимизации инфокоммуникационной системы, в которых функции стоимости отдельных компонентов сети представлены монотонными функциями. Тогда для локализации экстремума могут быть использованы методы "Деления отрезка пополам", "Золотого сечения" и "Чисел Фибоначчи".

Во многих случаях функция стоимости меняется скачкообразно. Например, при расширении емкости коммутационной станции свыше портов добавляется новое устройство электропитания, что приводит к росту стоимости оборудования на величину . Дальнейший рост емкости станции до порога 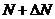не меняет величину стоимости оборудования. Как только емкость станции превысит величину 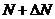, стоимость оборудования возрастет на величину .

На рисунке 13.1 показаны три графика, отражающие изменение удельных затрат на создание сети доступа и ее элементов – . Индекс " " принимает одно из трех значений. Для коммутационной станции , для абонентского кабеля , а для сети доступа в целом . Все три функции , по своей природе, ступенчатые.

Рис. 13.1. Три графика функций

Точки и определяют область изменения емкости коммутационной станции. Они могут различаться в десять и более раз.

Для графика по оси абсцисс указаны значения , в которых стоимость порта коммутационной станции меняется скачком. Рост емкости коммутационной станции ведет к увеличению длины абонентской линии. Абонентский кабель поставляется так называемыми строительными длинами. Точки приращения стоимости АЛ определяются этими длинами – . Точки на оси абсцисс, в которых возможны приращения функции , образуют множество . 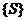Очевидно, что

. (13.6)

Функции и можно аппроксимировать непрерывными кривыми. Их анализ свидетельствует, что аппроксимирующие кривые монотонны. Это означает, что на отрезке [ ] будет иметь один минимум. Истинная (ступенчатая) функция , как следует из нижнего графика на рисунке 13.1, может иметь несколько минимумов и максимумов. На нижнем графике указаны соответствующие абсолютные значения. Не исключено, что замена функций и непрерывными кривыми приведет к существенной ошибке в определении минимума исследуемой зависимости.

Для множеств и целесообразно найти наибольшее общее кратное – 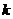. Тогда преобразование Лапласа-Стилтьеса для исследуемой функции – может быть представлено суммой:

. (13.7)

В этой формуле 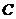– некая константа, значение которой не существенно для определения минимума функции , а коэффициенты определяются изменениями функций и в точках .

Контроль суммы по 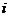позволяет легко выделить то значение , когда наступает абсолютный минимум функции . Существенно то, что область минимального значения функции лежит в диапазоне шириной не менее чем . Ширина этого диапазона определяется значением емкости коммутационной станции, в котором имеет место следующее приращение функции .

Дата добавления: 2018-02-15; просмотров: 590; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!