Annex 1. Общие понятия теории телетрафика
Заявки, поступающие в систему телетрафика, образуют поток. В редких случаях поток заявок можно считать детерминированным. Тогда время между поступлением соседних заявок – постоянная величина. Процесс поступления заявок обычно является случайным. Полной характеристикой случайной величины считается функция распределения 
. В электросвязи часто используется гипотеза о том, что число поступающих заявок за время 
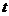подчиняется пуассоновскому распределению. Это утверждение эквивалентно экспоненциальному распределению функции :
. (A1.1)
Величина 
называется интенсивностью потока заявок. Среднее время между поступлением соседних заявок 
определяется следующим образом:
. (A1.2)
Длительность обслуживания заявок, как правило, также является случайной величиной с функцией распределения 
. Простейшие модели телетрафика предполагают, что функция подчиняется экспоненциальному распределению:
(A1.3)
Величина называется интенсивностью обслуживания заявок. Среднее время обслуживания 
определяется так:
. (A1.4)
|
|
|
По количеству обслуживающих приборов системы телетрафика делятся на однолинейные и многолинейные. Типичным примером однолинейной системы (один обслуживающий прибор) служит общий канал сигнализации. Пучок соединительных линий между двумя коммутационными станциями описывается многолинейной системой телетрафика.
При использовании алгоритма обработки заявок с ожиданием обычно задается число мест для формирования очереди 
. Если 
, то система работает по алгоритму с потерями. При 
число мест для ожидания не ограничено. Такая идеализация иногда вполне допустима, если вероятность потери мала. Тогда гипотеза о возможности создания бесконечной очереди позволяет существенно упростить анализ систем телетрафика.
При использовании приоритетного обслуживания необходимо определить тип алгоритма обслуживания заявок.
На рисунке A1.1 приведена классификация приоритетного обслуживания. Основным классификационным признаком служит тот тип приоритета, который используется для обработки заявки. Заявки могут обрабатываться без приоритета. Такой алгоритм характерен, например, для устройств управления электромеханических коммутационных станций. Приоритетные стратегии обработки заявок можно разделить на три основные группы, которые следует рассмотреть подробно. Заметим, что комбинированные алгоритмы предусматривают переход к приоритетному обслуживанию при определенных условиях (например, резкий рост трафика, приводящий к снижению показателей качества обслуживания).
|
|
|
Рис. A1.1. Классификация алгоритмов обслуживания заявок
Для анализа приоритетных стратегий целесообразно ввести простую модель. Все заявки делятся на группы, которым присваивается приоритет от 1 до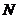 
. Заявка с приоритетом 
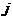имеет преимущество перед заявками, которым присвоены приоритеты с 
до .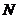
В системе с относительными приоритетами обслуживание заявок не прерывается. Допустим, заявка с приоритетом 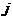застала все обслуживающие приборы занятыми. Тогда она встает в очередь перед всеми заявками, имеющими более низкий приоритет. Среди заявок с приоритетом 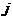она будет последней.
Системы с абсолютными приоритетами основаны на прерывании обслуживания заявок. Такая возможность предусмотрена для всех случаев, когда обслуживаются заявки более низкого приоритета. При этом могут использоваться три основных варианта возобновления прерванного процесса обслуживания заявок.
|
|
|
В некоторых случаях используются смешанные приоритеты. Тогда множество 
разбивается на несколько классов – 
. Чем меньше индекс у класса 
, тем выше абсолютный приоритет у обслуживаемых заявок. В пределах каждого класса заявкам могут назначаться относительные приоритеты.
Понятие "алгоритмы обслуживания заявок" включает также способы их выбора из очереди. Классификация основных алгоритмов выбора заявок на обслуживание приведена на рисунке A1.2.
Рис. A1.2. Классификация алгоритмов выбора заявок на обслуживание
Случайный выбор заявок на обслуживание позволяет отказаться от каких-либо процедур формирования очереди. В инфокоммуникационных системах этот алгоритм используется редко. Обслуживание в порядке очереди – классический алгоритм выбора заявок из очереди. Он известен по англоязычным аббревиатурам FIFO (First In, First Out) и FCFS (First come, first served). Выбор заявки на обслуживание из конца очереди обычно используется в системах, подобных складам, но применяется также и в сетях связи. Этот алгоритм известен по аббревиатурам LIFO (Last In, First Out) и LCFS (Last come, first served).
|
|
|
В теории телетрафика часто используется аббревиатура ЧНН – час наибольшей нагрузки. Он определяется как непрерывные 60 минут суток, в течение которых – в среднем – наблюдается максимальная телефонная нагрузка. Для достоверного выявления ЧНН в телефонной сети необходимо провести большой объем измерений. Обычно регистрация нагрузки осуществляется с интервалом в 15 минут.
В некоторых случах – в дополнение к ЧНН – выделяется период наибольшей нагрузки. Его длительность ( 
) может быть различной в зависимости от цели, для которой необходимо знать период максимальной нагрузки. Она может быть меньше или больше одного часа – рисунок A1.3. В данном примере составляет три часа.
Рис. A1.3. Час и период наибольшей нагрузки
Иногда измеряется также час наибольшей интенсивности вызовов. Эта величина представляет интерес для оценки процессов функционирования устройств управления, входящих в состав коммутационных станций.
Доля нагрузки, создаваемой в ЧНН – 
, часто оценивается коэффициентом концентрации – 
. Для его расчета необходимо также знать нагрузку за сутки – 
:
. (A1.5)
Диапазон изменения этого коэффициента значителен. Для многих телефонных сетей в крупных городах он составляет около 0,1. В менее крупных сетях величина может достигать 0,2. Если рассмотреть два населенных пункта, находящихся в таких часовых поясах, для которых разница во времени составляет половину суток, то коэффициент концентрации для используемого пучка междугородных каналов будет очень большим.
[1] В этой лекции используется ряд терминов из теории телетрафика. Основные понятия, используемые в теории телетрафика приведены в Приложении 1 к этой лекции.
Дата добавления: 2018-02-15; просмотров: 317; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!