Пропускная способность транспортных ресурсов
Пропускная способность сети и ее элементов[1]
Постановка задачи
Модель сети в виде графа, использованная в предыдущей лекции, удобна для решения только части задач, касающихся анализа и синтеза телекоммуникационной системы. В первую очередь модели в виде графа полезны для выбора структуры сети. Для решения задач, относящихся к характеристикам оборудования коммутации и передачи, модели в виде графа не всегда уместны. Одна из группы важных задач, которая не решается при помощи теории графов, – оценка пропускной способности сети и ее элементов.
Словосочетание "пропускная способность" не всегда адекватно отражает ту функцию, о которой идет речь. Для уточнения соответствующих терминов целесообразно обратиться к простой модели, показанной на рисунке 9.1. Эта модель, например, хорошо описывает процесс функционирования коммутационной станции в ТФОП. В ее составе устройство управления (Control unit) служит моделью для тех аппаратно-программных средств, которые выполняют логические задачи обслуживания вызовов. Управляемое устройство (Controlled unit) – модель коммутационного поля, через которое устанавливаются соединения. Часто вместо слова "устройство" используется термин "система".
Рис. 9.1. Простейшая модель коммутационной станции
Для управляемой системы пропускная способность оценивается количеством соединений, которое может быть установлено. Чаще всего используется термин "capacity". Иногда специалисты оперируют конкретной количественной оценкой. Например, для коммутационной станции в ТФОП пропускная способность может измеряться в Эрлангах. Это название было предложено в честь датского ученого А.К. Эрланга (A.K. Erlang), который внес большой вклад в развитие теории массового обслуживания. На самом деле Эрланг – безразмерная величина, численно равная количеству одновременно занятых приборов обслуживания.
|
|
|
Вспомним аналогию со стаканом сока, введенную на первой лекции. Задача расчета пропускной способности для управляемой системы может рассматриваться как выбор стакана, требуемого объема. Если объем стакана меньше, чем объем сока, то часть продукта будет потеряна. Если выбрать стакан очень большого объема, то затраты на перенос сока будут чрезмерно высокими. Целесообразно найти разумный компромисс. Обычно допускается потеря небольшой части вызовов. Для оценки характера потерь анализируются процессы, обозначенные на рисунке 9.1 как 
и 
.
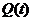Для управляющей системы пропускная способность оценивается, в первую очередь, скоростью обработки вызовов. Для подобных задач обычно используются термины throughput и capability. Результаты измерений выражаются в вызовах за единицу времени. Для управляющей системы весьма существенны последствия, связанные с задержкой процессов обработки информации. Правда, и доля потерянных вызовов из-за малоэффективной работы системы управления также является важной величиной.
|
|
|
Вернемся к примеру со стаканом сока. Задача расчета пропускной способности для управляемой системы может рассматриваться как выбор оптимальной скорости переноса стакана с соком. Если скорость передвижения мала, то потребность в соке может отпасть. При чрезмерно большой скорости доставки следует ожидать роста затрат на реализацию данной процедуры. Речь снова идет о компромиссе. Необходимо определить разумные величины для задержек и потерь. Для их оценки следует анализировать процессы, обозначенные на рисунке 9.1 как 
и 
.
Пропускная способность элементов телекоммуникационной сети может рассматриваться как задача, прямо или косвенно связанная с анализом процессов , , 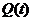и . Пропускная способность телекоммуникационной сети в целом – интегральная оценка, отражающая процессы функционирования всех элементов, которые образую сеть.
Пропускная способность транспортных ресурсов
|
|
|
Первые системы автоматической телеграфной и телефонной связи использовали алгоритм обслуживания вызовов с потерями. Если, например, через коммутационное поле (управляемая система) можно установить только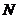 
соединений, то вызов под номером 
теряется. Необходимо установить следующее: какую долю вызовов можно потерять. На рисунке 9.2 показана типичная гистограмма количества поступающих вызовов за одни сутки. Очевидно, что надо анализировать период наибольшей активности абонентов.
Рис. 9.2. Распределение количества вызовов, поступающих за одни сутки
Ночью осуществляется незначительное количество вызовов. Ресурсы сети используются с низкой эффективностью. В дневное время количество вызовов заметно возрастает. Днем обычно наблюдается некоторое снижение активности абонентов. К вечеру количество вызовов снова возрастает. Эти процессы позволяют проследить определенные закономерности. Тем не менее, измерение за один и тот же час в разные дни показывает, что количество вызовов является случайной величиной. Диапазон изменения этой случайной величины может быть весьма существенным.
Рассчитать пропускную способность так, чтобы при максимальном количестве поступивших вызовов не было отказов в обслуживании, сравнительно просто. Предположим, что в результате измерений определено максимальное количество одновременно обслуживаемых вызовов 
. Это означает, что численность каналов, которые необходимы для обслуживания максимального количества вызовов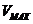 
, будет равна . Очевидно, что вероятность использования всех 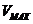очень мала. С другой стороны, исследование реакции абонентов показало, что вероятность отказа в обслуживании на уровне нескольких процентов вполне приемлема. Тогда реальное количество необходимых каналов 
может стать существенно меньше значения 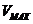. Это обеспечит экономичное построение сети. Следствием такого решения становится снижение тарифов на телекоммуникационные услуги.
|
|
|
Пунктирная линия на рисунке 9.2 разделяет обслуженные и потерянные вызовы. Допустим, что количество поступающих вызовов равно 
. Из них 
вызовов будут потеряны. Доля потерянных вызовов 
определяется очевидным соотношением:
. (9.1)
При неограниченном числе измерений величину можно рассматривать как вероятность потери вызовов. Она позволяет установить связь между процессами и 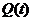. Вероятность устанавливается для периода наибольшей нагрузки. Поэтому процессы и 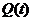также рассматриваются для этого отрезка времени. Иными словами, переменная 
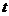не влияет на величину .
Произведение количества абонентов 
, числа вызовов, которое делает один абонент за час наибольшей нагрузки, 
и математического ожидания времени занятия 
называется интенсивностью трафика 
:
(9.2)
Датский ученый А.К. Эрланг (A.K. Erlang) в 1917 году вывел формулу, которая связывает величины , и количество используемых каналов :
. (9.3)
Если в качестве процесса рассматривать интенсивность трафика , то процесс 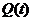представим простейшим соотношением 
. Данный пример отражает тривиальный случай зависимости процессов и 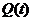. Более сложные примеры рассматриваются в четырнадцатой лекции.
Дата добавления: 2018-02-15; просмотров: 482; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!