Экстремум функции многих переменных (необходимое и достаточное условия).
Пусть задана функция двух переменных z=z(x,y), (x,y) 
D. ТочкаM0(x0;y0) - внутренняя точка области D.
Если в D присутствует такая окрестность UM0 точки M0, что для всех точек
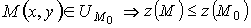
то точка M0 называется точкой локального максимума. А само значение z(M0) - локальным максимумом.
А если же для всех точек
то точка M0 называется точкой локального минимума функции z(x,y). А само значение z(M0) - локальным минимумом.
Локальный максимум и локальный минимум называются локальными экстремумами функции z(x,y). На рис. 1.4 поясняется геометрический смысл локального максимума: M0 - точка максимума, так как на поверхности z =z (x,y) соответствующая ей точка C0 находится выше любой соседней точки C (в этом локальность максимума).
Для начала рассмотрим необходимые условия экстремума функции, также определим понятие экстремума. Начнем с понятия экстремума:
Положим, что имеется некоторая функция с двумя переменными 
Определение: Точка 
называется точкой экстремума (максимума или минимума)
функции , если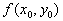 
есть соответственно наибольшее или наименьшее значение функции в некоторой окрестности точки .
При этом значение 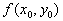называетсяэкстремальным значением функции (соответственно максимальным илиминимальным). Говорят также, что функция 
имеет в точке экстремум (или достигает в точке 
экстремума).
Заметим, что в силу определения точка экстремума функции лежит внутри области определения функции, так что функция определена в некоторой (хотя бы и малой) области, содержащей эту точку.
|
|
|
Какие из найденных точек действительно являются точками экстремума, мы установим после приведения достаточного условия экстремума.
Иногда удается, и, не прибегая к достаточным условиям, выяснить характер стационарной точки функции. Так, если из условия задачи непосредственно следует, что рассматриваемая функция имеет где- то максимум или минимум и пи этом системе уравнений (*) удовлетворяет только одна точка (т. е. Одна пара значений x и y), то ясно, что эта пара и будет искомой точкой экстремума функции.
Заметим, наконец, что точками экстремума непрерывной функции двух переменных могут быть точки, в которых функция недифференцируема (им соответствуют острия поверхности - графика функции).
Так, например, функция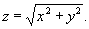 
имеет, очевидно, в начале координат минимум, равный нулю, но в этой точке функция недифференцируема; график этой функции есть круглый конус с вершиной в начале координат и осью, совпадающей с осью 
.
Следовательно, если иметь в виду не только дифференцируемые, но и вообще непрерывные функции, то нужно сказать, что точками экстремума могут быть стационарные точки и точки, в которых функция недифференцируема.
|
|
|
Вполне аналогично определяется понятие экстремума функции любого числа независимых переменных.
Совершенно ясно, что точка обычного экстремума (говорят также безусловного экстремума) является и точкой условного экстремума для любой линии, проходящей через эту точку. Обратное же, разумеется, неверно: точка условного экстремума может и не быть точкой обычного экстремума. Поясню сказанное обычным примером.
Дифференциальные уравнения. Основные понятия. Задача Коши.
Дифференциа́льноеуравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, 
не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.
Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
|
|
|
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные 
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
В математике и ее приложениях приходится рассматривать уравнения, в которых неизвестными являются функции. Так, задача о нахождении пути s (t) по заданной скорости vсводится к решению уравнения sʹ(t) = v (t), где v (t) — заданная функция, а s (t) — искомая функция.
Например, если v (t) = 3 - 4t, то для нахождения s (t) нужно решить уравнение sʹ (t) = 3 - 4t
Это уравнение содержит производную неизвестной функции. Такие уравнения называются дифференциальными.
|
|
|
Решить дифференциальное уравнение yʹ = x + 1.
∆ Требуется найти функцию y (x), производная которой равна x + 1, т.е. найти первообразную функции x + 1. По правилам нахождения первообразных получаем:
y = x²/2 + x + C,
где C — произвольная постоянная.
Дифференциальные уравнения, уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные. Теория Д. у. возникла в конце 17 в. под влиянием потребностей механики и других естественнонаучных дисциплин, по существу одновременно с интегральным исчислением идифференциальным исчислением.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при 
, а решение отыскивается при 
.
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение вида
или
называется дифференциальным уравнением с разделяющимися переменными.
Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.
Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение, чтобы в одну часть уравнения входили только функции от 
и 
, в другую часть уравнения - только функции от 
, 
. Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:
Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные и , могут быть потеряны решения, обращающие это выражение в ноль.
Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем получаемдванеопределенных интеграла.
Дата добавления: 2018-02-18; просмотров: 1092; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!