Метод подстановки и интегрирование по частям.
Асимптота графика функций. Общая схема исследования и построение графика функций
Аси́мпто́та (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность[2]. Термин впервые появился у АполлонияПергского, хотя асимптоты гиперболы исследовал ещё Архимед
Вертикальная асимптота — прямая вида 
при условии существования предела 
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
1. 
2. 
Горизонтальная асимптота — прямая вида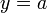 
при условии существования предела
.
Наклонная асимптота — прямая вида 
при условии существования пределов.
В других разделах было показано, что исследование функции f(x) на минимум и максимум, на точки перегиба облегчают построение графика этой функции. Но кривая y = f(x) может иметь асимптоты, т.е. прямые, к которым неограниченно приближается кривая по мере удаления ее переменной точки в бесконечность.
|
Определение. Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x).
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Пусть кривая y = f(x) имеет одну или несколько вертикальных асимптот (рис.1).
Для нахождения вертикальных асимптот кривой y = f(x) нужно отыскать такие значения x = a, при которых yобращается в бесконечность, т.е. при которых 
.
Уравнение вертикальной асимптоты будет
|
|
|
x = a (1)
В самом деле, непосредственно видно, что расстояние точки M(x; y) от прямой x = a равно d = | x - a |. Когдаx ® a, то точка M(x; y) движется по кривой y = f(x), удаляясь в бесконечность, причем ее расстояние d = | x - a | от прямой x = a стремится к нулю и, согласно определению асимптоты, прямая x = a является асимптотой кривой y = f(x)
Интеграл. Свойства интеграла
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.
Процесс нахождения интеграла называется интегрированием.
Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения.
Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является
|
|
|
Свойства интеграла:
∫F'(x)dx=∫dF(x)=F(x)+C
∫(αf(x)+βφ(x))dx=α∫f(x)dx+β∫φ(x)dx, α,β - постоянные
∫f(ax+b)dx=1aF(ax+b)+C
(∫f(x)dx)'=f(x)
∫abf(x)dx=-∫baf(x)dx
∫aaf(x)dx=0
∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx
∫aa+Tf(x)dx=∫0Tf(x)dx, где T - период функции f(x)
∫abf(x)dx≥∫abg(x)dx, если f(x)≥g(x)
|∫abf(x)dx|≤∫ab|f(x)|dx
m(b-a)≤∫abf(x)dx≤M(b-a), еслиm≤f(x)≤M
∫-aaf(x)dx=2∫0af(x)dx, если f(x) - четная
∫-aaf(x)dx=0, если f(x) – нечетная
Метод подстановки и интегрирование по частям.
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 
Сделаем подстановку 
где 
— функция, имеющая непрерывную производную.
Тогда 
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
|
|
|
Если u = u (х), v = v (х) - дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций d(uv) = udv+vdu получается формула интегрирования по частям
Эта формула применяется в случае, когда подынтегральная функция представляет собой произведение алгебраической и трансцендентной функций. В качестве и обычно выбирается функция, которая упрощается дифференцированием, в качестве dv — оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.
Для сведения данного интеграла к одной из формул простейших интегралов формулу нужно применить несколько раз. Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям.
Подстановкой в математике называется введение новой переменной. Подстановка позволяет свести решение неравенства или уравнения к двум или нескольким более простым неравенствам или уравнениям. Решая неравенство
f(x) < 0 (>, 
, 
), можно сделать подстановку либо всамим неравенстве, либо при решении уравнения f(x) = 0 (третий шаг метода интервалов). Поясним это на примере. Достаточно часто, используя метод постановки, удается понизить степень уравнения или неравенства.
|
|
|
Дата добавления: 2018-02-18; просмотров: 842; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!