Параллель тасмалдауы бар параллель сумматорлар. Компьютерлік схемотехниканың арифметикалық негіздері.
Лекция
Компьютерлік схемотехниканың арифметикалық негіздері.
Компьютердегі сандық ақпарат төмендегідей сипатталады:
- санау жүйесімен (екілік, ондық);
- сан түрімен (нақты, космплексті, массив);
- сан типімен (аралас, бөлшек, бүтін);
- сандарды көрсету аралығымен және дәлдігімен;
- терім сандарды кодтау әдістерімен;
- арифметикалық операцияларды орындау алгоритмдерімен.
Санау жүйесіне анықтама берейік: санау жүйесі– цифрлік белгілер (алфавит) жиыны көмегімен сандарды жазу әдістері мен ережелерінің жиыны. Цифрлік белгілердің санын санау жүйесінің негізі деп атайды.
Санау жүйесінің екі типі болады:
· позициялық,әрбір цифрдің мәні санды жазғандағы оның орнымен анықталады;
· позициялық емес, әрбір цифрдің мәні санды жазғандағы оның орнына тәуелді емес.
Позициялық емес санау жүйесініңмысалы римдік санау жүйесі болады: IX, IV, XVжәне с.с.
Позициялық санау жүйесіне күнделікті қолданылатын ондық санау жүйесін айтуға болады.
Позициялық жүйеде кез келген бүтін санды көпмүшелік түрінде жазуға болады:
Xs={AnAn-1...A1A0}s=An Sn+An-1Sn-1+...+A1S1+A0S0
мұндағы s – санау жүйесінің негізі;
А-осы санау жүйесінде жазылған санның мәндік
цифрлары;
n – санның разрядтар саны.
Мысал 1. 534110санын көпмүшелік түрінде жазайық:
534110=5×103+3×102+4×101+1×100
Мысал 2. 32110санын екілік санау жүйесінде жазайық. Ол үшін санды 2–дәрежелі сандардың қосындысы түрінде жіктеп жазу керек.
32110=1×28+1×26+1×20
Одан соң екі дәреже болған кездегі коэффициенттерін оңнан солға қарай жазамыз (минималды нөлінші дәрежеден максимал дәрежеге қарай)
Сондықтан бұл сан екілік санау жүйесінде 1010000012 түріне келеді.
Екілік санау жүйесіндегі сандармен орындалатын арифметикалық операциялар:
1. Қосу операциясы бір разрядта екілік қосу кестесі көмегімен орындалады:
+ 0 1
0 0 1
1 1 10
Мысал 3.
10012 11012 111112
10102 10112 12
100112 110002 1000002
2.Алу операциясы алу кестесі көмегімен орындалады, ондағы 1 үлкен разрядтан алынады.
- 0 1
0 0 11
1 1 0
Мысал 4.
1011100112 1101011012
1000110112 1010111112
0010110002 0010011102
3.Көбейту операциясы кәдімгі ондық санау жүйесіндегі сызба бойынша орындалады.
х 0 1
0 0 0
1 0 1
Мысал 5.
х 110012х 1012
11012 112
11001 101
11001 101
11001 11112
1010001012
4.Бөлу операциясы 10-ық санау жүйесінде пайдаланылатын алгоритмге ұқсас алгоритм бойынша жүргізіледі.
Мысал 6.
1010001012 11012 1000110002 11112
1101 11012 1111 100102
1110 0010100
1101 1111
1101 10102 -остаток
1101
0
Негізгі әдебиет: 1, 2, 3, 4.
Қосымша әдебиет: 11, 12
№2–лекция
Тақырып:ЭЕМ–де сандарды көрсету әдістері.
Біз білетіндей сандарды көрсетудің екі негізгі әдістері бар:бекітілген және жүзушіүтірі бар. Көптеген әмбебап ЭЕМ–дер жүзуші үтірі бар сандармен жұмыс істейді, ал көптеген арнайы ЭЕМ-дер бекітілген үтірі бар сандармен жұмыс істейді.
Бірақ машиналардың бірқатары екі форматтағы сандармен жұмыс істей береді.
Жалпы жағдайда сандарды көрсету әдісі бағдарламалау сипатына үлкен әсер етеді. Бекітілген үтірі бар жүйеде жұмыс істейтін ЭЕМ–де бағдарламалау қиын өйткені арифметикалық қиындықтан басқа үтірдің тұрған орнын анықтау керек.
Бекітілген нүкте. Машинаның разрядтық торында разрядтың тұрақты саны болады деп келісейік - n.
Бекітілген үтірі бар сандарды көрсеткен кезде үтір әрқашан да үлкен разрядтың алдында тұр деп есептеледі, ал есептеуге қатысатын барлық сандар абсолют өлшемі бойынша бірден кіші деп есептеледі:
|X| < 1Сандардың сипаттамаларын енгізейік: өзгеру аралығы және көрсету дәлдігі. 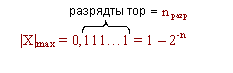 Өзгеру аралығы машина әрекет ететін сандардың орналаса алатын шектерімен сипатталады.
Өзгеру аралығы машина әрекет ететін сандардың орналаса алатын шектерімен сипатталады.
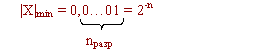 0-ге тең емес ең кіші сан:
0-ге тең емес ең кіші сан:
Осылайша ЭЕМ жұмыс істейтін сандар аралығы:
|X|min |X|
|X|  |X|max2-n
|X|max2-n  |X|
|X|  1 - 2-n
1 - 2-n Негізгі әдебиет: 1, 2, 3, 4.
Қосымша әдебиет: 11, 12
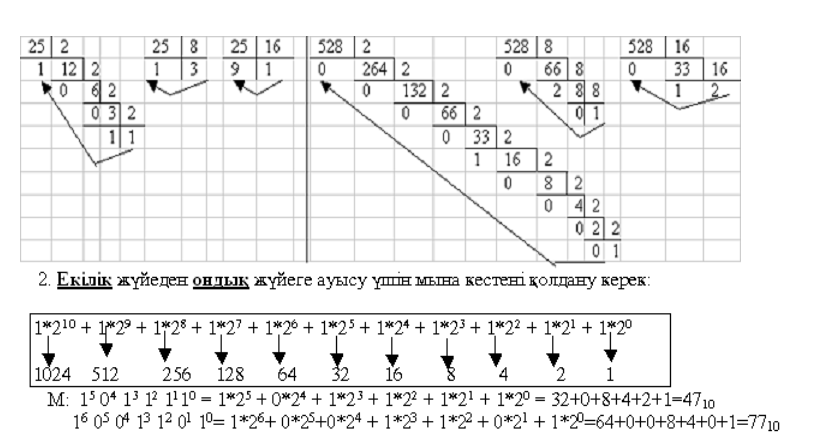
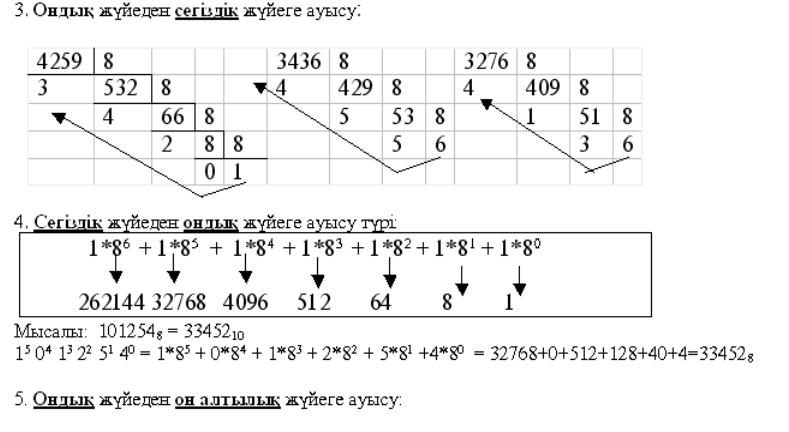
Тақырып: Компьютерлік схемотехниканың арифметикалық негіздері.
Компьютердегі сандық ақпарат төмендегідей сипатталады:
- санау жүйесімен (екілік, ондық);
- сан түрімен (нақты, космплексті, массив);
- сан типімен (аралас, бөлшек, бүтін);
- сандарды көрсету аралығымен және дәлдігімен;
- терім сандарды кодтау әдістерімен;
- арифметикалық операцияларды орындау алгоритмдерімен.
Санау жүйесіне анықтама берейік: санау жүйесі – цифрлік белгілер (алфавит) жиыны көмегімен сандарды жазу әдістері мен ережелерінің жиыны.









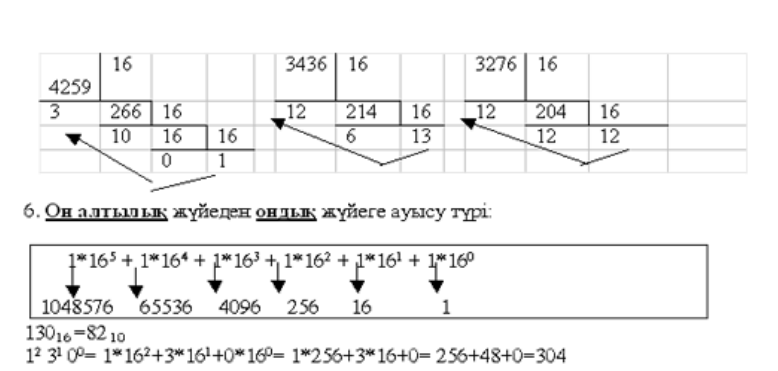

1.2.1Логика алгебрасының негізі қаңидалар1ы
Лекция
Тақырып:Компьютерлік схемотехниканың логикалық негіздері.
Кәдімгі алгебраданбасқа арнайы алгебра бар. Оның негізін ХІХ ғ. математигі Дж. Буль салған. Бұл алгебра пікірлерді есептеумен айналысады. Оның ерекшелігі дискреттік құрылғылардың жұмысын сипаттауға қолдану болып келеді. Ондай құрылғылар қатарына есептеу техникасы және автоматика құрылғыларының бір классы жатады.
Мұнда алгебраның өзі құрылғының үлгісі рөлін атқарады. Ол көрсетілген типтегі еркін құрылғының жұмысы осы алгебраның көмегімен қандай да бір жағынан тек қана сипатталуы мүмкін дегенді білдіреді. Шындығында нақты құрылғы физикалық логика алгебрасында сипатталғанан бөлек жұмыс істейді.
Логика алгебрасының функцияларына қатысты бірнеше синонимдер бар:
1. логика алгебрасының функциялары;
2. ауыстырып қосқыш функциялары;
3. бульдік функциялар;
4. екілік функциялар.
Қажеттілігінше бұл синонимдердің барлығын пайдаланамыз.
Аргументтердің қандай да бір жиынын қарастырайық:
<X1,X2,X3,...Хi,...Xn>және де аргументтердің әрқайсысы басқаларынан тәуелсіз екі мүмкін мәннің біреуін қабылдайды деп келісеміз. Xi = {0, 1}Әр түрлі логикалық айнымалылар бір бірмен функционалдық тәуелділікпен байланысқан болуы мүмкін. Функционалдық тәуелділік логикалық айнымалылар формулалармен немесе шындық кестесімен сипаттауға болады. Жалпыламалы түрде екі айнымалысы бар функциясының формласы мына түрде жазылады
y=f(X1, X2),мұндаңы X1, X2–кіретін айнымалылар. Шындық кестесінде кіретін айнымалылардың барлық терімділік комбинациялары және оларға сәйкес логикалық амалдар орындалған кейнгі функциялардың мәндері көрсетіледі.
Бір айнымалыда толық топтама төрт функциядан тұрады. Олар 2 кестеде көрсетілген.
2 кесте – Бір айнымалы функциясының толық топтамасы
| х | У1 | У2 | У3 | У4 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
Y1— Инверсия,Y2— Тепе-тең функция, Y3— Абсолют ақиқат функция и Y4 – Абсолют жалған функция.
Инверсия (емес,жоқ) ақпаратты цифрлік түрде өңдейтін құрылғыларда қолданатын негізгі логикалық функция болып саналады.
Екі айнымалыда толық топтама16 функциядан тұрады. Бірақ олардың барлығы түгелдей қолданылмайды. . Ақпаратты Цифрлық өңдейтін құрылғылыарда қолданатын екі айнымалының негізгі логикалық функцияларға мыналар жатады: инверсия, дизъюнкция, конъюнкция,mod2бойынша қосу, Пирс тілсызығы, Шеффер штрихі .
Жоғарда көрсетілген бір және екі айнымалы логикалық функцияларды іске асыратын логикалық амалдардың шарты белгілері 3 кестеде көрсетілген.
3кесте. Логикалық амалдардың аты мен белгісі
| Амалдың аты | сөз | Белгісі |
| инверсия | ЕМЕС (NOT) | 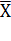 , -Х , -Х
|
| Дизъюнкция, логикалық қосу | НЕМЕСЕ (OR) | Х1 \/ Х0, Х1+Х0 |
| Конъюнкция, логикалық көбейту | ЖӘНЕ(AND) | Х1 /\ Х0, Х1 &Х0, Х1  Х0 Х0
|
| mod2 бойынша қосу (бірмәнділік емес) | ЖОҚҚА ШЫҒАРАТЫН -НЕМЕСЕ | (X1,X2)= X1ÅX2 |
| Пирс тілсызығы | НЕМЕСЕ-ЕМЕС | 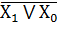 , , 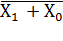
|
| Шеффер штрихі | ЖӘНЕ-ЕМЕС | 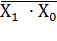 , , 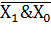
|
Инверсияамалын таза арифметикалық түрде орындауға болады: 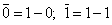 және алгебралық түрде:
және алгебралық түрде: 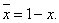 бұл мысалдан х инверсиясы, яғни
бұл мысалдан х инверсиясы, яғни 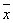 x-ті 1-ге дейін толықтырады. Сондықтан бұл амалдың таңы бір аты толықтырғыш. Осыдан мынандай тұжырымға келуге болады, қосарлы инверсия бастапқы аргументке әкеледі.
x-ті 1-ге дейін толықтырады. Сондықтан бұл амалдың таңы бір аты толықтырғыш. Осыдан мынандай тұжырымға келуге болады, қосарлы инверсия бастапқы аргументке әкеледі. 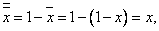 Бұл екі жақты бекерге шығару заңы болып аталады..
Бұл екі жақты бекерге шығару заңы болып аталады..
4 кесте – Екі айнымалылардың негізгі функцияларының ақиқат кестесі
| Дизъюнкция | Конъюнкция | шығарылып тасталғаннемесе | Пирс тілсызығы | Шеффер штрихы | ||||||||||
| Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
Дизъюнкция. Бір күрделі пікір оған кіретін пікірлердің кем дегенде біреуі ақиқат болған жағдайда ақиқат болады. X1 НЕМЕСЕ X2 деп оқылады:
Еркін құрылғыны синтездеу техникалық (физикалық) есебі ЛАФ–ын құру математикалық есебіне әкелінеді.
Дизъюнкция.Арифметикалық немесе алгебралық қосудан айырмашылығымұнда екі бірдің барлығы қортындысында бірді береді.Сондықтан логикалық қосуда + орнына мына таңбаны (∨) қолданылады.
Алғашқы екі жолы нольмен қосу ережесін анықтайды: x ∨ 0 = x, ал соңғы екі жолы бірмен қосу заңын анын анықтайды (x1 = 1): x∨ 1 = 1.
Конъюнкция.Екі пікірді алайық:
А=<Москва – РФ астанасы> В=<екі-екім төрт>онда А & В күрделі пікірі ақиқат болады, өйткені бұл екі пікір де ақиқат. Егер ақиқат пікірге '1' мәнін ал жалғанға '0' мәнін жазсақ онда пікірді көбейтінді деп айтуға болады. Бұл жағдайда конъюнкция үшін ақиқаттық кестесі көбейту кестесіне сәйкес келеді. ақиқаттық кестесінің алғашқы екі жолы нольге көбейту заңынx·0=0, ал соңғы екі жолы бірге көбейту заңын: x·1 = x көрсетеді.Конъюнкция функциясы екі пікір бір уақытта ақиқат болған жағдайда ғана ақиқат.Шығарылып тасталған немесе- бұл функцияның шығысында 1 пайда болады егерде, тек бір кірісінде бір болса.Егерде кірісінде бірдің саны бірден көбңрек болса немесе бүкіл кірісте ноль болса, шығыста ноль болады.Бұл арифметикалық қосуға ұқсас амал сондықтаноның аты mod2 бойынша қосу (бірмәнділік емес)және былай ⊕ белгіленеді.
Пирс тілсызығыи Шефферштрихі. Бұлар дизъюнкция и конъюнкция амалдарының инверсиясы сондықтан арнаулы белгілері жоқ Қарастырылған логикалық функциялар ақиқат мәні басқа функциялардың ақиқатығына байлынысты емес, тәуелсіз аргумент деп аталатын айнымалыға байлынысты, сондықтан қарапайым және элементар түрлерге жатады Цифрлық есептеу құрылғыларда элементар функциялар негізінде жасалған күрделі функциялар қолдынылады.Күрделі функцияның ақиқатығы осы күрделі функцияның аргументі болатын басқа функциялардың ақиқатығына байлынысты.
Мысалы, в күрделі логикалық функцияның 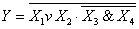 аргументері X1∨X2 және
аргументері X1∨X2 және  саналады
саналады
Лекция
Логикалық элементтер
Ақпаратты цифрлық өңдейтін құрылғыларда логикалық функцияларды жүзеге асыруға логикалық элементер қолдынылады. Жоғарғыда келтірілген функциялады
іске асыруға қолдылатын логикалық элементердің шарты графикалық белгілер 1 суретте көрсетілген.
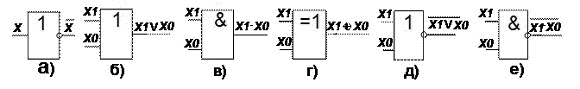
1 сурет.
Шарты графикалықбелгілері: а) ИНВЕРТОР(ЕМЕС), б) НЕМЕСЕ (ИЛИ), в) ЖӘНЕ (И), г) ШЫҒАРЫЛЫП ТАСТАЛҒАННЕМЕСЕ, д)НЕМЕСЕ-ЕМЕС(ИЛИ-НЕ), е)ЖӘНЕ-ЕМЕС(И-НЕ.)
Күрделі логикалық функциялар қарапаиым логикалы элементердің негізінде іске асырылады. Нақтылы аналитикалық функцияны іске асыру үшін оларды бір біріне сол функцияға сәйкес жалғастыру керек. Алдында көрсетілген 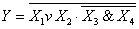 күрделі функцияны іске асыратын логикалық құрылғының функциональдық сұлбасы 2 суретте көрсетілген.
күрделі функцияны іске асыратын логикалық құрылғының функциональдық сұлбасы 2 суретте көрсетілген.
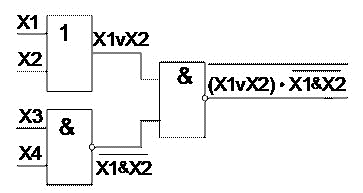
2 –сурет. Күрделі логикалық функцияны жүзеге асыруының мысалы. Қандай элементерден және қалай біріктіріп логикалық құрылғыны жасауға болатын, логикалық теңдеу көрсетінін 2 сурететен көруге боады. Логикалық теңдеу және функциональдық сүлбе бірмәнді сәйкес болғандықтан, логикалық функцияны алгебраның заңын қолдана отырып қарапайым күйге келтірген пайдалы болады, демек санын қысқартып немесе логикалық элементердің жүзеге асырғанда номенклатурасын өзгертуге болады.
Логика алгебрасының заңдары мен тепе-теңдіктері
Логика алгебрасының математика аппараты, логикалық өрнектерді түрлендіруге , элементердің санын қысқартып, элементер базаларын ауыстыруға мүмкүндүк береді.Заңдар:
1.Орынаустырымдылық: X ∨ Y = Y ∨ X;X · Y = Y · X.
2.терімділік: X ∨ Y ∨ Z = (X ∨ Y) ∨ Z = X ∨(Y ∨ Z);X · Y · Z = (X · Y) · Z = X· (Y· Z).
3. Идемпотентности:X ∨ X = X;X · X = X.
4. Үлестірімділік: (X ∨ Y)· Z = X· Z ∨ Y· Z.
5. Екі жақты( бекерге шығару:. 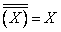
6.Екі жақтылық заңы (ДеМорган ережесі): 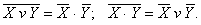
7.Структуралық формуларды түрлендіруге мынандай тепе-теңдіктер қолдынылады: X ∨ X · Y = X;X(X ∨ Y) = X— жұтылу ережесі.
X· Y ∨ X·  = X,(X ∨ Y)·(X ∨
= X,(X ∨ Y)·(X ∨  ) = X –желімдеу ережесі.
) = X –желімдеу ережесі.
Логикалық операциялардың орындалу реті.
1 терістеу— бірінші сатылы логикалық амал.
2 Конъюнкция— екінші сатылы логикалық амал.
3 Дизъюнкция— үшінші сатылы логикалық амал.
Егерде логикалық өрнекте бірнеше амалдар кездесетін болса, онда бірінші бірінші, содан кейін екінші , содан кейін үшінші сатылы амалдар орындалады. Бұл ережеден кез келген ауытқу жақшамен белгілену керек.
Лекция
Цифрлық құрылғылардың синтездеуінің негізі. Құрамдастырылған цифрлық құрылғылардың синтездеудегі амалдардың ретілігі. Құрамдастырылған цифрлық құрылғылар логикалық формуласының аналитикалық жазылуы.Базис түсінігі
2.1 Құрамдастырылған цифрлық құрылғылардың (ҚЦҚ) синтездеудегі опреациялаының ретілігі.
1.(ҚЦҚ) анықтамасына, қолдануының тағаиндалуына, жұмыс істеу принципінің сөздік сипамасына сәйкес ақиқат кестесінқұру.
2. Ақиқат кестесіне сәйкес логикалық формуласын құру.
3.Алынған формуланы әр түрлі вариант істеп оның ішінен түрлі критериге сәйкес ең жақсысын табу мақсатында талдау.
4.Және, немесе, емес элементерден ҚЦҚ функциональдық сұлбасының құруСоставление функциональной схемы КЦУ из элементов И, ИЛИ, НЕ.
2.2 Аналитическая запись логической формулы КЦУ
МДҚП пішінде жазу (Мүлтіксіз дизъюнктивті қалыпты пішін). МДҚП-да логикалық формула әр біріне бүкіл тәуелсіз айнымалылардан емесімен немесе олсыз кіретін бірнеше логикалық көбейтінділердің қосыдысынан тұратын өрнекті айтады.
Формуланы алу екі сатыда өтеді.
а)Бүкіл тәуелсіз айнымалылар кіретін көбейтінділердің қосындысы жазылады. Қосындылардың саны логикалық функция 1 болатын ақиқат кестесінен алынған жиындардың санына тең.;
б)алынған жиында қарастырылыған нольге тең тәуелсіз айнымалылардың үстіне инверсия белгісі қойыладыМКҚП пішінде жазу. (Мүлтіксіз конъюнктивті қалыпты пішін ).
МКҚП пішінде формула бүкіл айнымалылар емесумен немесе онсыз кіретін логикалық бірнеше қосындылардың көбйтіндісіне тең.
Алдыңғы жағдайдағыдай формуланы алу екі сатыда өтеді:
а) Барлық көбейтінділердің логикалық көбейтіндісі жазылады; көбейтінділердің саны логикалық функция 0 болатын ақиқат кестесінен алынған жиындардың санына тең;
б)алынған жиында қарастырылыған бірге тең тәуелсіз айнымалылардың үстіне инверсия белгісі қойылады.
ҚЦҚ және МКҚП түрдегі формулар эквивалентіжәне логика алгебрасының заңдарының көмегімен бірінен- біріне түрлендіруге болады.
Мысал:Үш кірісі бар мажоритарлы логикалық элементті синтездеу керек. Шығу күйі кіріс сигналдардың көбімен сәйкес келетін логикалық элементті мажоритарлы деп атайды.
Мажоритарлы элементің сөздік сипатамасын негізіндегі құрылған оның ақиқат кестесі. (5 Кесте).
5 Кесте – мажоритарлы элементің ақиқат кестесі
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Ақикат кестесінің негізінде МДҚПжәне МКҚПфункциялары жазылады, сосын функциональдық элементің сұлбасы құрастырылады.МДҚП 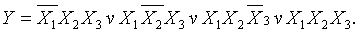
МКҚП: 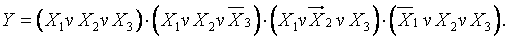

3 сурет Мажоритарлық элементің функциональды сызбасы.
.Бұл сұлба 8 элементен тұрады.Жалпы кірісінің саны 19-ға тең.Кірісінің саны сұлбаның күрделілігін сипатайды және Квайнша сан деп аталады. МКҚП негізінде құрылған функцияда 19 кірісі болады..
2.3 базис түснігі.
Кез келген күрделі функция ақиқат кестесімен , МДҚПнемесеМКҚП беріледі. Осы формулалардың кез келгені логикалық қосу, көбейту және жоққа шығару жаылады. Сондықтан цифрлық сигналдарды өңдеуді іске асыратын логикалық құрылғыларды жалпы жағдайда ЖӘНЕ,НЕМЕСЕ, ЕМЕС операциялар орындайтын элементер міндетті түрде болу керек. Мұндай элементердің жиынтығы функциональды толық логикалық элементер жүйесі немесе логикалық базис деп аталады.
Бұл мынаны білдіреді. ЖӘНЕ,НЕМЕСЕ, ЕМЕС элементердің комбинациялары жеткілікті түрде алып кез келген күрделі цифрлық құрылғы жасап шығаруға болады.. ЖӘНЕ,НЕМЕСЕ, ЕМЕС элементерден тұратын базис негізгі деп аталады.
Бірақта мұндай жүйеде керек элементердің санын не ЖӘНЕэлементін болмаса НЕМЕСЕ элементін шығарып керекті элементердің санын азайтуға болады.
Мысалы, Морган теоремасына сәйкес мыны өрнекті алайық 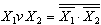 . Бұл өрнекте НЕМЕСЕ логикалық амалын айнымалардың инверсті міндерінін ЖӘНЕ амалымен
. Бұл өрнекте НЕМЕСЕ логикалық амалын айнымалардың инверсті міндерінін ЖӘНЕ амалымен  ,нәтижесіне инверсия амалын қолданып
,нәтижесіне инверсия амалын қолданып 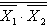 ,НЕМЕСЕ элементін шығарып тастауға болады. (4сурет).
,НЕМЕСЕ элементін шығарып тастауға болады. (4сурет).
4 сурет. НЕМЕСЕ элементін ЕМЕС,ЖӘНЕ элементерімен іске асыру.
Дәл солай айнымалардың инверсті мәндеріне логикалыұ ұосу амалын қолданыпсодан кейін инверсия амалын қолданып ЖӘНЕ элементін шығарып тастауға 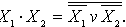 болады.
болады.
Демек екі элементерден тұратын (НЕМЕСЕ,ЕМЕСәлде ЖӘНЕ,ЕМЕС)жүйелер функциональды толық жүйелер болып саналады және минимальды логикалық базистен құрылады.. Минимальды логикалық базиспен функциональды толық жүйелерді сұлба түрде іске асыру үшін универсальды НЕМЕСЕ-ЕМЕС,ЖӘНЕ-ЕМЕС,ЖӘНЕ-НЕМЕСЕ-ЕМЕС логикалық элемЕнтерді қолдану жолымен іске асырылады(5сурет).
5 суретУниверсальды(Әмбебап)логикалық элементтер
НЕМЕСЕ-ЕМЕС элементі. 5сурет,а) Пирс тілсызығы деп аталатын логикалық оерацияны іске асырады 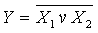 . Шеффер штрихі деп аталатын логикалық операцияны іске асыратынЖӘНЕ-ЕМЕС элементІ И-НЕ (5,б сурет). Және-немесе-емес элементі (5,всурет) осуществляет операцию
. Шеффер штрихі деп аталатын логикалық операцияны іске асыратынЖӘНЕ-ЕМЕС элементІ И-НЕ (5,б сурет). Және-немесе-емес элементі (5,всурет) осуществляет операцию 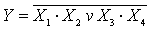 операциясын іске асырады және күрделі базистің элементі болып саналады.
операциясын іске асырады және күрделі базистің элементі болып саналады.
Универсаль базистің элементері негізгі үш амалды іске асыруғамүмкіндік береді. (6сурет). Мысалы ЕМЕС амалын ЖӘНЕ-ЕМЕС элементің көмегімен іске асыру үшін кірістерін біріктіру жеткілікті.Например, для осуществления операции НЕ с помощью элемента -НЕ достаточно объединить входы 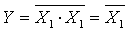 (рисунок6,асурет). НЕМЕСЕ-ЕМЕС элементі үшін дәл солай істеу керек.
(рисунок6,асурет). НЕМЕСЕ-ЕМЕС элементі үшін дәл солай істеу керек.
6 сурет. ЕМЕС,ЖӘНЕ,НЕМЕСЕ функцияларын ЖӘНЕ-ЕМЕС элементерімен іске асыру.
ЖӘНЕ-ЕМЕС пен инверторды тізбектей жалғағанда логикалық көбейту амалы іске асырылады: 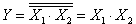 (6,бсурет). Дәл осылай қосылған НЕМЕСЕ-ЕМЕС элементер логикалық көбейту амалын іске асырады:
(6,бсурет). Дәл осылай қосылған НЕМЕСЕ-ЕМЕС элементер логикалық көбейту амалын іске асырады: 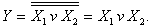
Екеуі кірістері біріктірілген, инвертор режимінде істейтін үш ЖӘНЕ-ЕМЕС элементер логикалық қосу амалын іске асыруға мүмкіндік береді (6,в сурет),  . Үш НЕМЕСЕ-ЕМЕСэлементерді жалғастырып логикалықкөбейту амалын іске асыруға болады
. Үш НЕМЕСЕ-ЕМЕСэлементерді жалғастырып логикалықкөбейту амалын іске асыруға болады 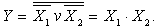
Жалпы жағдайда логикалық функция Y бірнеше айнымалыларға тәуелді X1,X2,…,Xn. Функция анықталған деп аталады егерде барлық айнымалылар үшін оның мәні белгілі болса. Функция анықталмаған деп аталады, егерде есеп шарты бойынша оның кейбір аинымалар терімділері мүмкін болмаса.Бұл жағдайда оны іске оңай асыру үшін оған ноль немесе бір жазып қосымша анықтап жіберуге болады.
Лекция
Логикалық формулаларды минималдау. Минималдаудың есептеу әдісі. Анықталмаған логикалық функциялардың минималдау. Әмебап базистерде құрлымдық формулалар жазу.
Логикалық құрылғының функциональдық сұлбасынан логикалық формулалардың күрделігінің бірмәнді тәуелділігі логикалық құрылғылардың құрлысының формуласын ықшамдау керектігін кажет ететін кортындыға ікеледі. Минималдау үрдісі логика алгебрасының теоремалары мен заңдары және негізгі байланыстарды қолдана отырып іске асырылады.
3.1 Ықшамдап есептеу әдісі.
Бұл әдістің мәні мынада: жүйелі түрде кейбір формулаға логика алгебрасының заңдарын, тепе теңдік ережелерімен өзгерту. .Және бұл жағдайда МДҚП кіретін біреуін немесе бірнешеуін қосу, 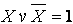 көбейткіштері бар, желемдеу ережесін және тағы басқа әдістер қолдынылады.
көбейткіштері бар, желемдеу ережесін және тағы басқа әдістер қолдынылады.
Мысал: Мажоритарлы элементің МДҚП түрде жазылған функциясын ықшамдау және оның сұлбасын негізгі базисте іске асыру.
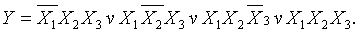
Бірінші үш минитермді төртіншімен желімдеп мажоритар элементіңДҚП функциясын аламыз.Бұл функция алғашқыға қарағанда қарапайымдылау.:
Y = X1·X2∨X1·X3∨X2·X3
Минималданғанмажоритарлы элменттің функциональдық сұлбасы 7 суретте көрсетілген.
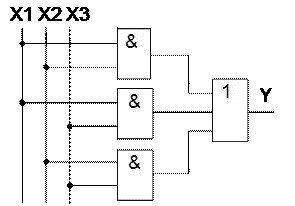
7сурет Ықшамдалған дезъюнктивті қалыпты пішіндегі функция негізінде іске асырылған мажоритарлы элементің функциональдық сұлбасы.3 және 7 суреттегі сұлбаларды салыстыра отырып квайн санының ықшамдалған сұлбада 19 дан 9 дейін кемігенін көреміз
Карно картасысымен ықшамдау әдісі.
Карно картасы –логикалық функциялардың ақиқат кестесін графикалық түрде көрсетілуі. Оның 2n көзі болады,мұндағы n-логикалық айнымалардың саны.Мысалы үш айнымалы функцияның Карно картасының көзі 2n=23=8, ал төрт айнымалы үшін— 24=16. Мынаған зейін аудырыңдар.Бағаналардың(егер n>3, дәл сондай жолдарыда)табиғи түрде екілік кодтың өсуіне байланысты емес белгіленеді. Кіретін айнымалардың мәніне сәйкес, карта координаталар жүйесімен белгіленеді. Бағаналар координатасы былай өзгереді:00 01 11 10, яғни көрші сандар жиынтығы бір бірінен бір цифрмен кез келген разрядта айырмашылғы болу ерек.
Ықшамдау үрдісі мағанасы мынада: 2k (k –бүтін сан) көзі бар тік бұрышты салу.Көрші элементар көбейтіндісіне (бір разрядта айырмашылығы бар) сәйкес көрші көздер тік бұрышқа біріктірледі.
Карно картасы жазықтықта кескінделген мен, квадратардың көршілері тордың бетінде орнатылады. Картаның жоғарғы және төменгі шекарасын желімдегенде цилиндр бетін құрады. Бүйір шекараларын желімдегенде тор беті пайда болады.
Мысал: Ақиқат кестесімен берілген үш айнымалы функцияны ықшамдау керек ( 6кесте).
6 кесте. Үш айнымалы функцияның ақиқат кестесі.
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
МДҚФ функция: 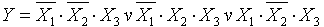
Карно картасын құрамызда және жанжағын белгілейміз.
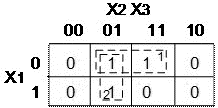
8 сурет. 3 айнымалы функцияға жазылған Карно картасы.
Карно картасында екі тік бұрыш құрамыз.Біріншісі екі бірінші минитермді (қосындысын)біріктіреді(жақшаға алады),екіншісі жоғарда көрсетілген МДҚП-ның ықшамдалатын функциясының бірінші және үшіншіқосыныдысы.Тік бұрышқа біріктірілген минтермдера айырмашылығы тек бір разрядта ғана.Ықшамдалғанда есептеу әдісімен жақшаның сыртына олардың өзгермейтін бөлігі функцияның ықшамдалған мәні:
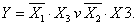
Сөитіп Карно картасымен көмегімен бір көбейтіндіге айырмашылығы бар, элементар көбейтінділері көрші көздерде орналастыруға болады
Ықшамдау алгоритмі. (Ықшамдаудағы қимылдардың реттігі.):
1. Карно картасы кескәнделеді де және қабырғалары белгіленеді.
2. Функция бір мәнін қабылдайтын айнымалар жиынтығына сәйкес көздерді бірмен, ал қалғандарын нольмен толтырамыз.
3. картаны тік бұрышпен жабудың ең жақсы вариантын қабылдайды. Тік бұрыштардың саны аз болу керек, мұндай вариант бірнеше болса, оның ішінен тік бұрыштардың ең үлкен аудан беретіні таңдап алынады.
Мысал: Карно картасымен берілген төрт айнымалылы функцияны ықшамдаңдар: (9сурет).
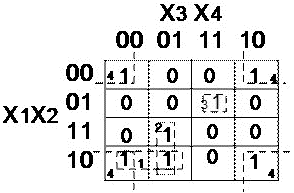
9сурет.
Төрт айнымалылы функциясының Карно картасы
Карно картасынан функцияның ықшамдалған түрін жазамыз:
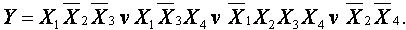
3.2 Анықталмаған логикалық функцияларды ықшамдау.
Егерде функцияның кіретін айнымалыларда тиым салынған жиынтықтар бар болатын болса, және оларың әрқайсысында да функция бірге немесе 0 тең болатын болса, ондай функция анықталмаған деп аталады.Ыңғайлы Ықшамдау үшін оны қосымша анықтау керек, яғни Карно картасында анықталмаған мәндерін өз еркімен «1» немесе «0» аиырбастау керек.Для удобства минимизации её следует доопределить, то ест ь неопределённые значения карты Карно произвольным образом заменить «1» либо «0».
Егер функцияда m тиым салынған жиынтықтары бар болса,толықтыру вариантардың саны 2mболу мүмкін.Ықшамдалған функцияның қарапайымрақ болатын вариантын таңдап алған қажет.
3.3Құрылымдық формулаларды универсал (әмбебап) базистерде жазу.
ЖӘНЕ-ЕМЕС базисінде жазу екі кезеңде өтеді:
а) Негізгі базисте ықшамдалған логикалық формула ДҚП пішінде көрсетіледі.
б) Алынған формуланың оң бөлігінің үстіне инверсияның екі белгісі қойылады да және де Моргана формуласымен ЖӘНЕ-ЕМЕС базисіне өту жүзеге асырылады.
Мысал. ЖӘНЕ-ЕМЕС базисінде мажоритарлы логикалық элементтің функциясын жазыңыз:
Бұлекі кезеңде өтеді:
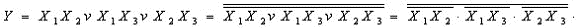
НЕМЕСЕ-ЕМЕС базисінде жазу
а) Негізгі базисте ықшамдалған логикалық функция КҚП пішінде көрсетіледі
б) Алынған формуланың үстіне инверсияның екі белгісі қойылады және және де Моргана формуласымен НЕМЕСЕ-ЕМЕС базисіне өту жүзеге асырылады.
ЖӘНЕ-НЕМЕСЕ-ЕМЕС базисінде жазу екі сатыда өтілетін:
а)  функциясының ниверсиялық мәнінің логикалық формуласы негізгі базисте ықшамдаладыда және ДҚП пішінде көрсетіледі.
функциясының ниверсиялық мәнінің логикалық формуласы негізгі базисте ықшамдаладыда және ДҚП пішінде көрсетіледі.
Логическая формула для инверсного значения функции  минимизируется в основном базисе и представляется в форме ДНФ.
минимизируется в основном базисе и представляется в форме ДНФ.
б) ЖӘНЕ-НЕМЕСЕ-ЕМЕС базисіне өту үшін формуланың екі бөлігінеде инверсия белгісі қойылады да , Морган формуласыменЖӘНЕ-НЕМЕСЕ-ЕМЕС базисіне өткізледі.
Мысал:

Лекция
Логикалық элементтер. Логикалық элементтердің негізгі параметрлері. Транзистор-транзисторлық логика. Қарапайым инвенторлы ТТЛ ЖӘНЕ-ЕМЕС элементі. Күрделі инвенторы бар ТТЛ элементі. ТТЛШ элементтері. Үш шығыс жағдайы бар ТТЛ.
4.1 Логикалық элементтердің негізгі параметрлері.
- кіріс бойынша бірігу коэффициенті Коб — логикалық функцияны іске асыратынкірістердің саны.
- шығу бойынша тармақталу коэффициенті Краз құрылғының бұл топтамадағы логикалық шығыс санының біруақытта берілген логикалық элементтің шығысына жалғанатындығын көрсетеді.
- Жылдам әсер етуі ЛЭ арқылы белігінің таралу уақытының бөгелуімен сипатталады және кіріс және шығыс белгілерінің графиктерімен анықталады (сурет 10). ЛЭ t1,0зд.р –ні қосқан кезде белгілінің таралу уақытын, t0,1зд.р –нің сөнген кездегі белгісінің уақытын және t1,0зд.р ср таралуының орташа уақытын ажыратады.
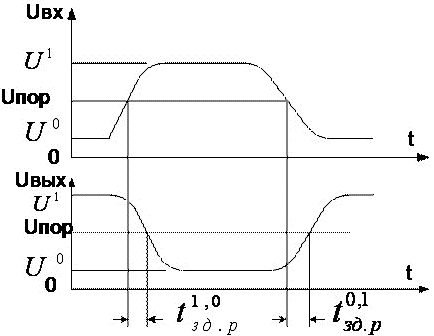
Сурет 10. ЛЭ белгісінің таралу уақытын анықтау
Белгінің таралуының орташа уақыты деп логикалық элементті қосқан және сөндірген кездегі белгінің таралу уақытының жартысына тең уақыт аралығын айтады.
tзд.р ср = (t1,0зд.р + t0,1зд.р)/2
- жоғарғы U1 және төменгі U0 деңгейлерінің кернеуі және олардың рұқсат етілетін тұрақсыздығы. U1 және U0 ретінде «Лог.1» және «Лог.0» кернеулерінің номиналды мәндері түсініледі; тұрақсыздық қатысты бірліктер немесе пайызда көрініс табады.
- жоғарғы U1 және төменгі U0 деңгейлерінің шекті кернеуі. Шекті кернеуі ретінде логикалық элементтің басқа жағдайға ауыса бастайтын сәйкес деңгейлер түсініледі. Бұл параметрлер сәйкес топтамадағы параметрлердің температуралардың жұмыс диапазонындағы орналасуымен анықталады, көптеген анықтамаларда ол UПОР ретінде беріледі.
- кіріс токтарыI0вх, I1вх төменгі және жоғарғы деңгейлердегі кіріс кернеулеріне сәйкес келеді.
- кедергіге қалыпты қарсы тұратындық. Статикалық кедергіге қалыпты қарсы тұратын қасиет қатысты шекті мәндердің кіріс және шығыс белгілерінің мәндері арасындағы минималды айырмашылық ретіндегі логикалық элементтің сипаттамалары бойынша бағаланады.
U-ПОМ = U1вых.min – UПОР
U+ПОМ = UПОР – U0вых.min
Әдетте, анықтамалық мәліметтерде пайдаланған кезде ЛЭ-ге ауыстырмайтын кедергінің бір ғана рұқсат етілетін мәні келтіріледі.
- Тұтынылатын қуаттылық Pпот немесе тұтыну тогы Iпот.
- Ауысу энергиясы – бір ғана ауысуды орындауға жұмсалатын жұмыс. Бұл әртүрлі топтамалар мен технологиялардың микросызбаларын салыстыруға қолданылатын интегралды параметр.
4.2 Транзисторлы-транзисторлық логика
Транзисторлы-транзисторлық логиканың элементтері (ТТЛ) орташа және жоғары жылдам әсер ету микросызбаларының базасын құрайды. Әртүрлі параметрлері болатын бірнеше сызба нұсқалары жасалған және оларқолданылады.
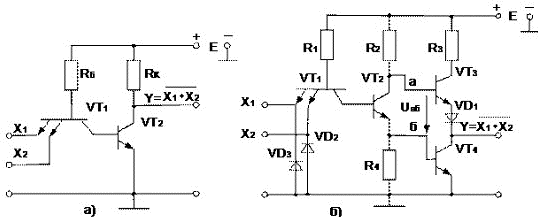
Сурет 11. Қарапайым а) және күрделі б) инверторы бар ЖӘНЕ-ЕМЕС логикалық элементтері
4.2.1 Қарапайым инверторы бар ЖӘНЕ-ЕМЕС ТТЛ элементі
Мұндай элементтің құрамына ЖӘНЕ логикалық операциясын орындайтын көпэмиттерлі транзистор VT1 (сурет 11,а) мен ЕМЕС операциясын жүзеге асыратын транзистор VT2 кіреді.
Көпэмиттерлі транзистор (КЭТ) ТТЛ-дің негізі болып табылады. КЭТ эмиттерлерінде U0=UКЭ.нас бар болған кезде эмиттерлі ауысымдар тікелей бағытта жылжыған және VT1 арқылы транзистор байытылған режимде тұруға жеткілікті болып саналатын базалық ток IБ1=(E–UБЭ.нас–UКЭ.нас)/RБ өтеді.
Егер кіріс кернеуін барлық кіріс орындарында U0 деңгейінен арттыратын болсақ, онда базадағы кіріс кернеуі Uб=Uвх+UКЭ.нас=UБЭ.нас кезінде артады және транзистор VT2 ашылатын болады. Алдағы уақыттағы UВХ артуы транзистордың VT1 эмиттерлі ауысымдарының жабылуына әкеліп соқтыратын болады, нәтижесінде ол коллекторлы ауысым тікелей бағытта ауысатын режимге, ал эмиттерлі ауысым кері бағытқа ауысады. Сызбаның шығысындағы кернеуі UВЫХ=UКЭ.нас=U0 (байытылған кездегі транзистор VT2).
Осылайша, қарастырылған элемент ЖӘНЕ-ЕМЕС операциясын жүзеге асырады.
ТТЛ элементтерінің қарапайым сызбасында бірқатар кемшіліктер бар. Мұндай элементтерді кезекпен-кезек қосатын болсақ, элементтің шығысында осындай басқа да элементтердің эмиттерлері қосылған кезде ЛЭ-ден тұтынылатын ток артады, ал жоғары деңгейдегі кернеу азаятын болады. Сондықтан элемент төмен жүктелімді қабілетке ие. Бұл ЛЭ-ден транзистор-жүктелімдермен тұтынылатын инверсты режимдегі көпэмиттерлі транзистордың үлкен эмиттерлі тогымен байланысты.
Сонымен қатар, бұл сызба оң кедергіге қарағанда аздаған кедергіге қарсы тұра алатын қасиетке ие: U+ПОМ=UБЭ.нас–U0=UБЭ.нас–2UКЭ.нас. Көрсетілген кемшіліктерді жою үшін күрделі инверторы бар ТТЛ сызбасы қолданылады (сурет 11,б).
4.2.2 Күрделі инверторы бар ТТЛ элементтері
Күрделі инверторы бар ТТЛ сызбасы да, қарапайым инверторы бар ТТЛ да ЖӘНЕ-ЕМЕС логикалық операциясын орындайды.
Қарастырылған режимге ТТЛ логикалық элеметінің аймағы сәйкес келеді (сурет 12,а).
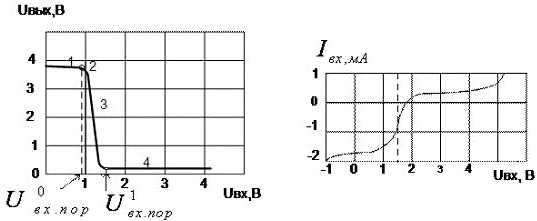
Сурет 12. 155 топтамадағы базалық ЛЭ-нің сипаттамасы: а - беріліс, б – кіріс
Барлық кірістегі кернеу артқан кезде VT2 базаның әлеуеті артады және UВХ=Uпор кезінде транзистор VT2 ашылады, коллекторлы ток IK2 R2 және R4резисторлары арқылы өте бастайды. Нәтижесінде базалық ток VT3 азаяды, ондағы кернеудің азаюы артады және кіріс кернеу азаяды (сурет 12 аймақ 2). Резисторда R4 кернеудің UR4<UБЭ.нас азаюы болған сәтте транзистор VT4 жабық болады. UВХ=U¹пор=2UБЭ.нас–UКЭ.нас болған кезде транзистор VT4 ашылады. Алдағы уақыттағы кіріс кернеуінің артуы VT2 және VT4-ның байытылуына, сонымен қатар, VT1 инверсты режимге ауысуына әкеледі (сурет 12 аймақ 3). Бұл ретте «а» нүктесінің әлеуеті (сурет 11,б) Ua=UБЭ.нас+UКЭ.нас тең, ал «б»-Uб=UКЭ.нас нүктесі сәйкесінше Uаб=Uа–Uб=UБЭ.нас тең. Транзисторды VT3 және диодты VD1 ашу үшін Uаб≥2UБЭ.нас қажет. Бұл шарт орындалмайтындықтан, онда VT3 және VD1 жабық болады және сызба кірісіндегі кернеу UКЭ.нас=U0 тең (сурет 12 аймақ 4).
Ауысқан кезде уақыт аралықтары орын алады. Бұл ток амплитудасын шектеу үшін аздаған кедергісі бар резисторды сызбаға қосады (R3=100–160 Ом).
Теріс кедергілер әсерінен ЛЭ-ні қорғау үшін сызбаға 0,5–0,6В деңгейде шектейтін диодтар VD2, VD3 енгізілген.
(4–4,5) В-дан асқан оң кернеу кезінде кіріс ток артады. ТТЛ ЛЭ-нә тәжірибеде қолданған кезде пайдаланбаған кірістерді бос қалдыруға болады. Алайда бұл ретте кедергіге қарсы қабілеттілік азаяды. Сондықтан олар әдетте алдыңғы ЛЭ үшін артуға әкелмесе, не өзара бірігеді, немесе R=1 кОм резисторы арқылы кіріс тогын шектейтін +5 В қуат көзіне жалғанады. Әр резисторға 20 кіріске дейін қосуға болады. Осылайша лог «1» деңгейі қолдан жасалады.
Күрделі инверторы бар ТТЛ элементінің кедергіге қарсы тұратын қасиеті:
U+пом = U1пор – U0 = 2UБЭ.нас – 2UКЭ.нас
U–пом = U1 – U1пор = E – 4UБЭ.нас + UКЭ.нас
Сигналдың таралу уақытымен анықталатын ТТЛ элементтерінің тез әсері негізгі емес тасымалдаушылардың жинақталу және таралу үдерісінің ұзақтығына тәуелді болып келеді. ТТЛ элементінің жұмысы кезінде ашық транзисторлар байытылу жағдайында тұратындықтан, ТТЛ инерттілігінің артуына транзисторлардың жабылу кезінде туындайтын негізгі емес тасымалдаушылардың таралу уақыты септігін тигізеді.
ТТЛШ элементтері
ТТЛ элементтерінің әсерін тездету мақсатында ТТЛШ элементтерінде Шотка транзисторлары қолданылады, ол қарапайым транзистор және база мен транзистордың коллекторы арасында қосылған Шотка диодының қосылысынан тұрады. Шотка диодындағы кернеудің азаюы қарапайым p-n-ауысымына қарағанда ашық жағдайда аз болғандықтан, кіріс тогының айтарлықтай бөлігі диол арқылы өтіп, ал аз бөлігі базаға енеді. Сондықтан транзисторлар терең байытылу режиміне кірмейді.
Сәйкесінше , коллекторлы ауысым арқылы инжекциялар үшін базада тасымалдаушылардң жинақталуы орын алмайды.
Шотка диодтары бар ТТЛ элементтеріндегі белгі таралуының орташа уақыты ТТЛ-дің қарапайым элементтеріне қарағанда 2 есе аз. ТТЛШ-ны кемшілігі ретінде ТТЛдің ұқсас элементтеріне қарағанда кедергіге қарсы тұра алу қасиетінің төмендігі жатады.
4.2.4 Үш шығыс жағдайы бар ТТЛ элементтері – қосымша кірісі бар V (сурет 13,а). Беріліс кезінде кернеу кірісіндегі U0 транзистор VT5 ашық және байытылған болады, ал транзисторлар VT6 және VT7 жабық және сондықтан да логикалық элементтің жұмысына әсер етпейді. Ақпараттық кірістегі белгілердің комбинациясына байланысты ЛЭ-де «лог.0» және «лог.1» деңгейіндегі белгілер болуы мүмкін.
13,б суретте бұл элементтің УГО-сы көрсетілген. ∇ белгісі кірістегі үш жағдайды көрсетеді. E∇ « Үшінші жағдайдың рұқсаты» белгісі ЛЭ-нің  =0 үшінші жағдайға ауысатындығын көрсетеді.
=0 үшінші жағдайға ауысатындығын көрсетеді.
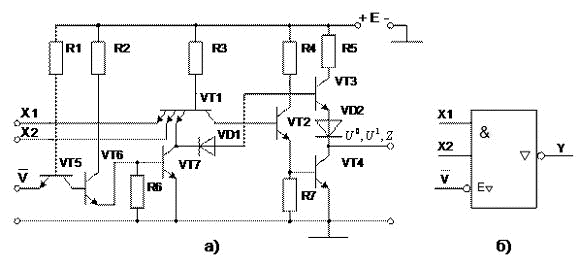
Сурет 13 үш шығыс жағдайы бар ЖӘНЕ-ЕМЕС логикалық элементі а) және оның УГО-сы б) .
Кесте 7-де ЛЭ ТТЛ кейбір топтамаларының параметрлері келтірілген.
Кесте 7 ЛЭ ТТЛ кейбір топтамаларының параметрлері
| ПАРАМЕТРЛЕР | ТОПТАМАЛАР | ||||
| Әмбебап | Жылдам әсер етуші | Микроқуатты | |||
| 133, 155 | К531 | КР1531 | К555 | Кр1533 | |
| Кіріс ток I0ВХ, мА | -1,6 | -2,0 | -0,6 | -0,36 | -0,2 |
| Кіріс ток I1ВХ, мА | 0,04 | 0,05 | 0,02 | 0,02 | 0,02 |
| Шығыс кернеу U0ВЫХ, В | 0,4 | 0,5 | 0,5 | 0,5 | 0,4 |
| Шығыс кернеу U1ВЫХ, В | 2,4 | 2,7 | 2,7 | 2,7 | 2,5 |
| Шығыс бойынша тарату коэффициенті KРАЗ | 10 | 10 | 10 | 20 | 20 |
| Кіріс бойынша біріктіру коэффициенті KОБ | 8 | 10 | — | 20 | — |
| Белгінің таралу уақыты tЗАД.ср | 19 | 4,8 | 3,8 | 20 | 20 |
| Тұтынылатын ток, мА: | |||||
| I0ПОТ( U0ВЫХ кезінде) | 22 | 36 | 10,2 | 4,4 | 3 |
| I1ПОТ( U1ВЫХ кезінде) | 8 | 16 | 2,8 | 1,6 | 0,85 |
| Кедергінің рұқсат етілетін кернеуі, В | 0,4 | 0,3 | 0,3 | 0,3 | 0,4 |
| Қуат кернеуі, В | 5 | 5 | 5 | 5 | 5 |
| Шығыс токтары, мА: | |||||
| I0ВЫХ | 16 | 20 | 20 | 8 | 4 |
| I1ВЫХ | -0,4 | -1 | -1 | -0,4 | -0,4 |
| Элементке шаққандағы орташа тұтынылатын қуаттылық, мВт | 10 | 19 | 4 | 2 | 1,2 |
5. Эмиттерлі-байланысқан логика. Тікелей байланысы бар транзисторлы логика (ТББТЛ)
Эмиттерлі-байланысқан логиканың негізі болып жылдам әсер етуші ток ауыстырғыш жатады (сурет 14,а). Ол екі транзисторлардан тұрады, мұндағы коллекторлы шынжырға RК жүктемесінің резисторлары кіреді, ал екі транзистордың да эмиттер шынжырына жалпы резистор Rэ кіреді.
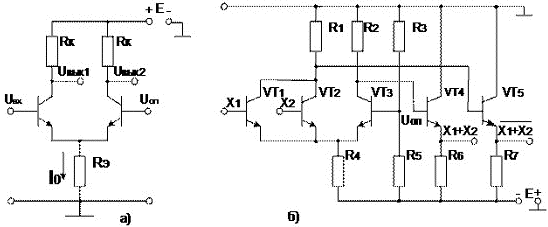
Сурет 14. Эмиттерлі-байланысқан логика: а) токты ауыстырғыш; б) қарапайым принципиалды сызба
Uвх артқан кезде ток транзистор арқылы көбейеді. Кернеу артады, транзистор VT2жабылады және ол арқылы ток та азаяды. Uвх лог «0» деңгейіне дейін азайған кезде керісінше транзистор VT1 жабық, ал транзистор VT2 байыту аймағымен шекаралас жерде сызықтық режимде болады.
ЭБЛ сызбасында (сурет 14,б) транзисторға VT1 параллельді түрде тағы бір немес бірнеше транзисторлар қосылады.
UВЫХ1 = U1 – UБЭ.нас = U0
UВЫХ2 = UПИТ – UБЭ.нас = U1
Осылайша, бірінші шығыс бойынша берілген сызба НЕМЕСЕ-НЕ логикалық операциясын, ал екіншісі бойынша НЕМЕСЕ операциясын жүзеге асырады. Шекті кернеу UПОР=UОП, логикалық ауысым ΔU=U1-U0=UБЭ.нас және сызбаның кедергіге қарсы тұра алу қасиеті U+ПОМ=U-ПОМ=0,5UБЭ.нас екендігі белгілі.
6. Интегралды инжекциялық логика. МТЖ (металл-тотық-жартылай өткізгіш) транзисторлардағы логикалық элементтер. Динамикалық жүктемесі бар кілттердегі логикалық элементтер. Комплементарлы кілттердегі логикалық элементтер.
Интегралды инжекторлы логика (И²Л) элементтерінің дискретті сызба техникасында дәл осындай ұқсас элементі жоқ және ол тек қана интегралды түрде жүзеге асырылуы мүмкін (сурет 16а). И²Л элементтері екі транзисторлардан құралады: көлденең орналасқан p-n-p-транзистор инжектордың ролін орындайды, ал тігінен орналасқан n-p-n-транзистор инвертор режимінде жұмыс жасайды. N-типті жалпы аймағы p-n-p-транзисторының базасы ретінде де, сондай-ақ n-p-n-транзисторының эмиттеры болып та қызмет етеді және «жерге қосылған» нүктеге жалғанады. p-n-p-транзисторының коллекторы мен n-p-n-транзисторының базасы да жалпы аймаққа жатады. Эквиваленттік сызба 16 б суретінде келтірілген.
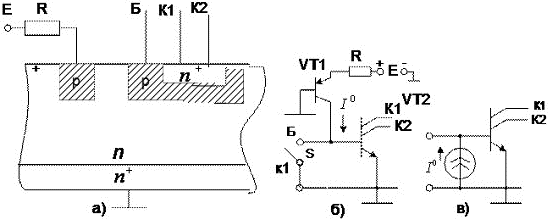
Сурет 16 Инжекциялық қуаттануы бар транзистор: а – құрылымдық сызба; б – эквиваленттік сызба; в – ток генераторы бар эквивалентті сызба.
Инжектордағы эмиттер-базаның байланысына UҚУАТ қуат көзінің кернеуі беріледі. Қуат көзінің минималды кернеуі эмиттерлік ауысымға кернеудің төмендеуімен анықталады: UКЭ.нас=0,7 В. Алайда, I0 эмиттер тогын тұрақтандыру үшін қуат көзімен қатар R резисторы да қосылады және қуаттау көзінің кернеуі алынады UҚУАТ =1…1,2 В. Бұл ретте p-n-ауысым эмиттер-база VT1 ашық және коллекторлы ауысымда тесік диффузиясы орын алады. Коллекторға жылжу шамасына қарай тесіктердің бір бөлігін электрондармен бірге қайта құрамдастырады, бірақ олардың айтарлықтай бөлігі коллекторлы ауысымға жетіп, одан өте бере инвентордың р-базасына (транзистор VT2) жетеді. Бұл диффузия үдерісі, яғни база тесіктердің инжекциясы кіру әсеріне қарамастан тұрақты түрде жүріп отырады.
Егер базадағы кернеу VT2 Uвх=U0, ал бұл S кілтінің тұйық жағдайына сәйкес, онда инвертордың р-базасына кіретін тесіктер қуаттау көзінің теріс полюсіне қарай кедергісіз жинақталады. Транзистор VT2-нің коллектор байланысына ток енбейді және ол коллекторлы байланыс VT2-нің ажыратылған жағдайына бара-бар болып саналады. Шығушы байланыстың мұндай жағдайы лог. «1» кернеуіне сәйкес келеді.
Uвх=U1 кезде (S кілті ажыратылған) инвертордың р-базасындағы тесіктер жинақталады. Базаның әлеуеті арта бастайды және сәйкесінше ауысымдар ашылмайынша ауысым VT2-гі кернеу де түсе береді. Ол жағдайда транзистор VT2-нің коллекторлы байланысында ток жүретін болады және эмиттер мен инвертор коллекторының арасындағы әлеуеттың әртүрлілігі нөлге жақындайдығ яғни бұл транзистор байланыстың қысқа тұйықталған аумағын танытатын болады, және бұл жағдай лог. «0» деңгейіне сәйкес келетін болады. Осылайша, жоғарыда қарастырылған элемент кілттің ролін атқарады.
Жалпы базамен сызбаға қосылған транзистордың коллекторлы тогы кең көлемде коллектордағы кернеудің өзгерісіне тәуелді болмайды. Транзистор VT1 жалпы базасы бар сызбаға қосылды. Биполярлы транзистор жұмысының теориясынан эмиттердің тұрақты тогы кезінде алынған оның сипаттамасы көлденеңге дерлік екендігі белгілі, яғни коллектордың тогы коллектордағы кернеуге тәуелді болмайды. Сондықтан ол токтың баламалы генераторымен ауыстырылуы мүмкін. Токтың эквивалентті генераторы туралы теоремаға сәйкес, тұрақты кернеу кезінде токты көбейту немесе қуат көзінен ажырату бұл генератордың ток мөлшеріне әсер етпейді. Осыған сәйкес, инжекциялық қуаттылығы бар транзистордың сызбасы сурет 16 в келтірілген қарапайым эквивалентті сызбаны танытады.
Егер Uвх=U1 , онда I0 тогы ток генераторынан VT2 базасын аша отырып ағылатын болады. Бұл ретте Uвх=U0. Егер Uвх=U0, онда I0 тогы жерге тұйықталады, транзистор VT2 жабық және Uвых=U1.
I0 инжекция тогының күші көп емес (10 нА…100 мкА), сондықтан транзистор белсенді режимде жұмыс жасайды. Белгіні тарату кедергісінің орташа уақыты тек инвертор базасындағы артық зарядтарды жұту үдерісінің ұзақтығымен және паразитті сыйымдылықты қайта қуаттау уақытымен ғана анықталады, сондықтан кілт жылдам қызмет етуші болып саналады. Кілт қызметінің жылдамдығы инжекция тогын арттырған кезде көбейе түседі.

Сурет 17 Интегралды инжекторлы логика (И²Л): НЕМЕСЕ-ЕМЕС элементінің сызбасы а) және логикалық ЖӘНЕ функциясын жүзеге асыру б).
Көп коллекторлы транзисторды қолдану жалпы коллекторлы ток VT2-ні бір ұқсас элементке кіруді басқару үшін жеткілікті болатын бірнеше бірдей үлестерге бөлуге мүмкіндік береді. Осыған орай, сурет 17,а көрсетілген НЕМЕСЕ-ЕМЕС логикалық элементінің қарапайым сызбасын қолдану мүмкін болып саналады. Бұл сызба НСТЛ (сурет 15, а қара) элементтерінің сызбасына ұқсас. НЕМЕСЕ-ЕМЕС НСТЛ элементтерінің сызбасына қарағанда НЕМЕСЕ-ЕМЕС И²Л элементінде тіпті біріктілірген коллекторлар байланысындағы резистор да талап етілмейді, себебі коллекторлы байланыс ток генераторынан келесі каскадқа ие болады.
Сурет 17,б-да ЖӘНЕ логикалық функциясын жүзеге асыратын сызба келтірілген. Екі кіреберіске (Х1 және Х2) лог. «0» белгісінің берілуі кезінде инверторлардың біріктірілген коллекторларында (VT3 және VT4) лог. «1» белгісі болады. Бір кіреберіске немесе екеуіне де бір уақытта лог. «1» белгісі берілетін болса, онда сызбаның шығысында лог. «0» аламыз, бұл ЖӘНЕ логикалық операциясының орындалуына сай болып келеді.
И²Л элементтері аз орын алады, қуаттылық пен ауысым энергиясын болмашы ғана тұтынады. Оларға келесідей параметрлер тән: UПИТ=1 В; tзад.ср=10…100 нс; Kраз=3,5; Kоб=1.
6.1. МТЖ-транзисторларындағы логикалық элементтер
МТЖ-транзисторларындағы логикалық элементтерде транзисторлардың тек екі типі ғана қолданылады: басқарушы және жүктеме. Басқарушы – қысқа, бірақ жеткілікті дәрежеде кең арнасы бар, сондықтан аз қуат мөлшерімен басқарылады. Жүктеме: керісінше, ұзын, бірақ тар арнасы бар, сондықтан жоғары шығу кедергісіне ие және үлкен белсенді кедергі ролін атқарады.
Биполярлы транзисторлардағы логикалық элементтердің алдындағы МТЖ-транзисторларындағы логикалық элементтердің айтарлықтай артықшылықтарына тұтынылатын аз қуаттылық жатады. Алайда, шапшаңдығы жөнінен олар биполярлы транзисторлардағы сызбаларға қарағанда ақсайды. Бұл оларда салыстырмалы түрде паразитті сыйымдылық CЗИ және CСИ - пен ажыратылады, оларды қуаттауға бірталай уақыт қажет болып саналады. Сонымен қоса, ашық МТЖ-транзисторының шығыс қарсылығы биполярлыға қарағанда әлдеқайда аз, ал бұл жүктеме конденсаторын қуаттау уақытын арттырады және ЛЭ жүктеме қабілеттілігін шектейді.
6.2 Динамикалық жүктемесі бар кілттердегі логикалық элементтер
Динамикалық жүктемесі бар кілттердегі логикалық элементтер бір жүктеме және бірнеше басқарушы транзисторлардан құралады. Егер басқарушы транзисторлар параллельді қосылған болса, онда НСТЛ-гідей (сурет 15,а қара) НЕМЕСЕ-ЕМЕС логикалық операциясын орын алады, ал кезектілікпен қосылған жағдайда ЖӘНЕ-ЕМЕС (сурет 18,а,б).
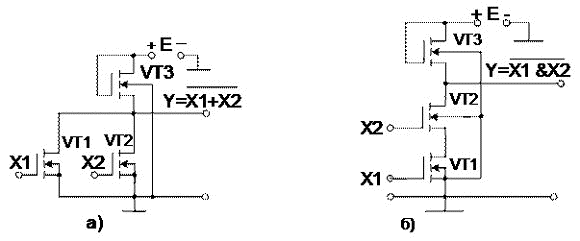
Сурет 18 МТЖ элементтерінің сызбасы: а) –НЕМЕСЕ-ЕМЕС; б) –ЖӘНЕ-ЕМЕС
Х1 және Х2 кіреберістеріндегі UВХ=U0<UЗИ.пор кернеуінің бар болған кезде басқарушы транзисторлар VT1 және VT2 жабық болады. Бұл ретте кернеу шығар кезде лог. «1» сәйкес келеді. Элементтің бір немесе екі кірісінде де UВХ=U1>UЗИ.пор қызмет етсе, онда шығар жерде лог. «0» орын алады, бұл НЕМЕСЕ-ЕМЕС логикалық операциясының орындалуына сай келеді.
ЖӘНЕ-ЕМЕС элементінің сызбасында басқарушы транзисторлар кезектілікпен қосылған, сондықтан сызбаның шығар жердегі лог. «0» деңгейі екі кірістегі де жекелеген белгілерде ғана орын алады.
6.3. Комплементарлы кілттердегі логикалық элементтер
Комплементарлы кілт әртүрлі типтегі өтімділік каналдары бар екі МТЖ-транзисторларынан тұрады, кірістері параллель, ал шығыстары кезекпен жалғанған (сурет 19,а). Кернеу болған кезде белгілі-бір типтегі арнасы бар транзистор үшін сәйкес транзисторды ашып, екіншісін жабу қажет. Қарама-қарсы полярлықтағы кернеу кезінде ашық және жабық транзисторлар орындарымен ауысады.Комплементарлы кілттердегі ЛЭ-ның бірқатар артықшылықтары бар.
Олар құрамына резисторлар кіретін ЛЭ үшін қолжетімсіз болып табылатын қуат көзінің кернеуінің өзгерісі кезінде жақсы жұмыс жасайды.
Статикалық режимде комплементарлы кілттің ЛЭ-сы қуатты көп пайдаланбайды.Оларға сонымен қатар шығыс белгісінің тұрақтылық деңгейі мен оның қуат көзінің кернеуінен аздаған айырмашылығы; жоғары кіріс және аздаға шығыс кедергісі; басқа технологиялардың микросхемаларымен оңай ұштасуы тән.
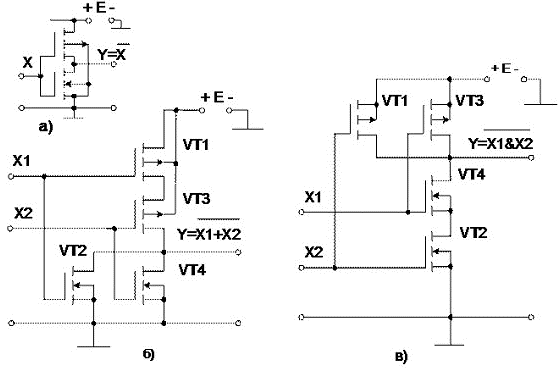
Сурет 19. КМТЖ ТЛ логикалық элементтерінің сызбасы: а) инвертор; б) НЕМЕСЕ-ЕМЕС; в) ЖӘНЕ-ЕМЕС.
2НЕМЕСЕ-ЕМЕС функциясын орындайтын КМТЖ ЛЭ сызбасы сурет 19, б-да көрсетілген. Транзисторлардың VT1, VT2 р-типті каналы бар және нөлге жақын бекітпедегі кернеу кезінде ашық болады. Транзисторлардың VT2, VT4 n-типті каналы бар және үлкен шекті мәнге ие бекітпедегі кернеу кезінде ашық болады. Егер кірістің екеуінде де немесе біреуінде ғана лог. «1» деңгейі қызмет етсе, онда сызбаның шығысында лог. «0» белгісі болады, бұл НЕМЕСЕ-ЕМЕС операциясының орындалғанын көрсетеді.
Егер сатылап және параллельді қосылған транзисторлардың орнын ауыстырсақ, онда ЖӘНЕ-ЕМЕС функциясын орындайтын элемент жүзеге асырылатын болады (сурет 19, в). Ол алдыңғыға ұқсас түрде қызмет етеді. Транзисторлардың VT1, VT3 р-типті каналы бар және нөлге жақын бекітпедегі кернеу кезінде ашық болады. Транзисторлардың VT2, VT4 n-типті каналы бар және үлкен шекті мәнге ие бекітпедегі кернеу кезінде ашық болады. Егер осы транзисторлардың екеуін де ашатын болсақ, онда шығар жерде «лог.0» белгісі орнатылатын болады.
КМТЖ ЛЭ-де үш тұрақты жағдайы бар элементтерді жүзеге асыру оңай болып келеді. Ол үшін инвертордың транзисторларымен қатар инверсты белгілермен басқарылатын екі комплементарлы транзисторды VT1, VT4 біртіндеп қосады (сурет 20, а).
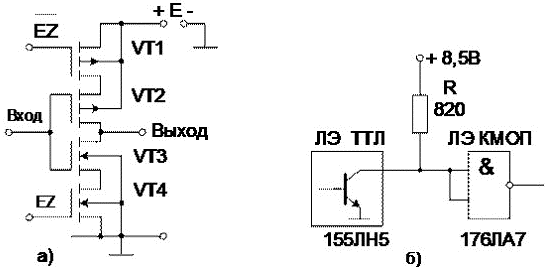
Сурет 20. Үш шығыс жағдайы бар инвертор а) ЛЭ ТТЛ-дың ЛЭ КМТЖ-мен келісілуі
б) ЛЭ ТТЛ-дың ЛЭ КМТЖ-мен келісілуін бірнеше тәсілдермен орындауға болады:
1) ЛЭ КМТЖ-ны аз кернеумен қуаттау (+5 В), бұл жерде ЛЭ ТТл белгілері ЛЭ КМТЖ транзисторларын ауыстырады;
2) ЛЭ ТТЛ-ны ашық коллектормен қолдану, шығу байланысына кернеудің қосымша көзіне жалғанған резисторлар қосылған (сурет 20,б).
Сақтау және монтаждау жүргізген кезде статикалық электр желісінен сақтанған жөн. Сондықтан сақтаған кезде микросхемалардың өткізгіші өзара тұйықталады. Монтажды сөнулі қуат кернеуі кезінде жүргізеді, бұл кезде де жөндеушілердің денесін жермен байланыстыратын білезіктерді қолдану қажетті болып саналады.
ЛЭ КМТЖ шағын және орташа жылдамдықтағы тиімді санды құрылғыларды тұрғызған кезде кеңінен қолданылады. ЛЭ КМТЖ топтамасының кейбір параметрлері 8-ші кестеде көрсетілген.
Кесте 8 ЛЭ КМТЖ кейбір топтамасының параметрлері
| Параметрлер | сериясы | |
| 176, 561, 564 | 1554 | |
| Қуаттың кернеуі UПИТ, В | 3…15 | 2…6 |
| Қажетті кернеу, В: | ||
| Төмен деңгейU0ВЫХ | <0,05 | <0,1 |
| Жоғары деңгей U1ВЫХ | UПИТ–0,05 | UПИТ–0,01 |
| Белгіні ұстап тұрудың орташа уақыты, нс: | ||
| для UПИТ=5 В | 60 | 3,5 |
| для UПИТ=10 В | 20 | — |
| Тосқауылдың жеткілікті кернеуі, В | 0,3 UПИТ | — |
| Статикалық режимде тұтынылатын қуаттылық, мВт/корпус | 0,1 | 0,1…0,5 |
| Кіріс кернеуі, В | 0,5…(UПИТ+0,5 В) | 0,5…(UПИТ+0,5 В) |
| Шығу токтары, мА | 1…2,6 | >2,4 |
| Ауысым жиілігінде тұтынылатын қуаттылық f=1 МГц, UПИТ=10 В, Cн=50 пф, мВт/корпус | 20 | — |
| Тактілі жиілік, МГц | — | 150 |
Лекция.
Комбинациялық типті цифрлық құрылғылар. Екілік сумматорлар (қосқыштар). Бір разрядты сумматорлар (қосқыштар)
Көп разрядты сумматорлар (қосқыштар). Арифметикалық логикалық құрылғылар.
Комбинациялық типті цифрлық құрылғылар немесе цифрлық жадысыз автоматтар деп шығысында логикалық мәндері оның кірісіндегі сигналдар жиынтығымен,немесе олардың комбинацияларымен бір мәнді анықталатын цифрлық құрылғылар аитады.
Оларға қосқыш сұлбалар, шифраторлар және дешифраторлар мультиплексорлар және демультиплексорлар, цифрлық компараторлар. Комбинациялық типті цифрлық құрылғылар немесе интегралды микросхема процессор, жады секілді үлкен интегральды микросхемалар құрамына кіреді.
7.1.1 Бір разрядты сумматорлар (қосқыштар)
Цифрлық есептеуіш техникада екі және үш кірісі бар қосатын сұлбалар қолдынылады және біршісі жартылай суматор, ал екіншісі толық бірразрядты суматор деп аталады.
Жартылай суматор тек сандардың кіші разрядтарын қосуға арналады.Толық бірразрядты суматорлардың алғашқы разрядтан келесі разрядқа көшіру үшін белгі беретін үшінші кірісі бар.
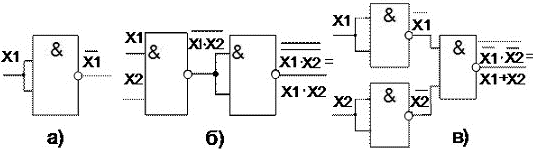
21 суретте а) жартылай суматорың ақиқат кестесі. 21 суретте б) негізгі базистің элементерімен осы кестенің негізінде МДҚП түрде жазылған құрылымдық формула.
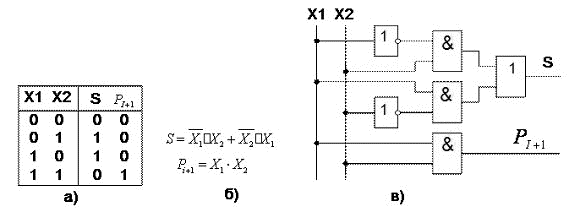
21сурет. Бір разрядты сумматор (қосқыш): а) ақиқат кестесі, б) құрлымдық формула, в) функциональдық сұлба.
Логикалық сұлбалардың сипатайтын сапалық көрсеткіштері болып мына негізгі параметрлер саналады:жылдамәсерлігі және құрылғыцның күрделісін көрсететін элементердің саны, жылдамәсерлігіэлементердің сұлбаның элементерін өткендегі сигналдың кешігу уақытының қосындысымен анықталады.Жоғарыда көрсетілген сұлбада жылдамәсерлігі үш логикалық элементте кідіруне байланысты.
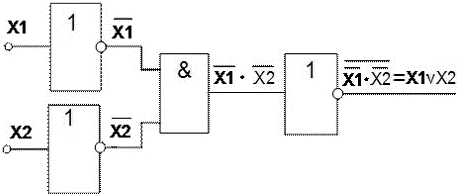
Көрсетілген сұлбаның 10 кірісі бар және 6 элементтен тұрады, яғни Кваин саны 10 тең. 21,в) суретте көрсетілген кемшілігі мынада.Оның кірісіне операндтың тура және инверісті мәндері берілу керек. Логика алгебрасының заңдарын қолдана отырып, кейбір операндтардың үстінен инверсияны алып тасатап түрлендіруге болады.Ұқшамдау реті 22,а) суретте,функциональдық сұлба-22, б) суретте, ал шартты графикалық белгісі 22,в) суретте көрсетілген.
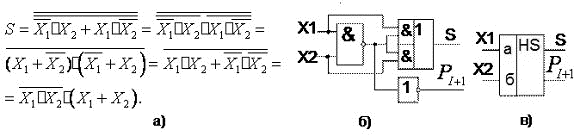
22сурет. Ұқшамдау ретіа), функциональдық сұлба, б) и шартты графикалық белгісі, в).бір разрядты жартылай сумматор.
Ықшамдалған сұлба жылдамәсерлі.Онды 6 элементің орнына 3элемент. Квайн саны 10-нан 7-ге дейін азайды.Егерде қосқыштардың саны өте көп екенін еске алсақ, ұтымның өте үлкен екенін білуге болады.
Толық бір разрядты қосындылағыштың сұлбасын екі жартылай суматордың негізінде немесе «НЕМЕСЕ» сұлбасының негізінде алуға болатынын 23,а суреттте көрсетілген.
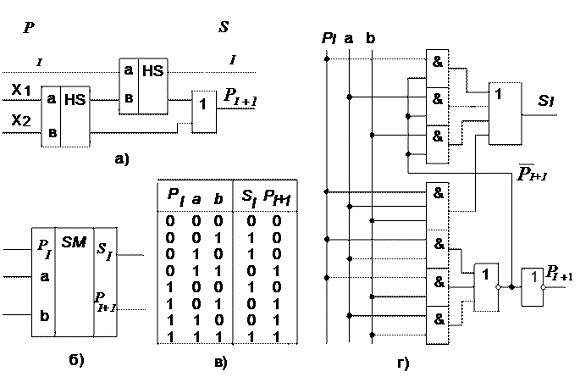
23сурет. Бірразрядты толық сумматор: а) екі жартылай сумматор негізінде жиналған функциональдық сұлба;функциональная схема на двух полусумматорах; б) — шарты гафикалық белгісі; в) — ақиқат кесстесі: г) — ықшамдалған сұлба.
23 суреттегі функциональдық сұлбаның жұмыс істеу приципінен ақиқат кестесін толтырамыз.Осы кестені талдаудан берілген сұлбаның толық бірразрядты сумматордың функциясын атқаратынын көруге болады.Өтетін сигнал екі тізбектелген жартылай сумматор сұлбаснан және немесе сұлбасынан өткендіктен бұл сұлбаның жұмыс істеу жылдамдығы ұтымды емес.
Суматорды екі шығысы және үш кіріс бар құрылғы түрінде істеген оның істеу әркетінің мақсатына сәйкес болареді.Оның функциясының МДҚП мына түрде жазылады.

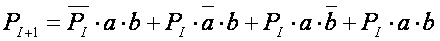
Интегралдық сұлбатехникада қолданылатын ықшамдалған мәндері:
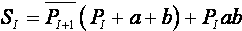
PI+1 = PIa + PIb + ab
Теңдеудің біріншісі логиканың алгебрасын қолдана отырып аналитикалық әдіспен, ал екіншісін- Карно картасының ықшамдау минимальдау әдісімен ықшамдалады. Бұл теңдеулерге сәйкес құрылған функциональдық сұлба23, г). суретінде көрсетілген. 23, а) суретіндегі сұлбаңа қарағанда жылдамырақ істейді.23, б). суретте толық бірразрядты сумматордың шарты гафикалық белгісі келтірілген.
7.1.2 Көпразрядты сумматорлар.
Көпразрядты сумматорлар жасау әдістері:
-тізбектеп қосу;
-тізбектеп тасымалдау параллель қосумен;
-параллель тасымалдау параллель қосумен.

24сурет. Көпразрядты сандарды қосу:а) -тізбектеп; б)параллель тізбектеп тасымалдаумен.
Тізбектеп қосу үшін барлық разрядтарға ортақ бір сумматор қолдынылады. 24,а сурет.
Операндтар аI және bI кірісі арқылы синхронды кіші разрядтан бастап енгізілу керек.
Кідірту тізбегі тасымалдауимпульсінің PI+1бір тактыға кететін уақыт ұзақтығындай сақтайды, яғнинымен қосылатын келесі разрядтың қосындылар жұбы келгенше.Кідіртуді D-триггер орныдайды.
Тізбектеп қосқанда, барлық разрядқа жалпы бір суматор қолдынылады.(24,а сурет) Кіші разрядтан бастап синхронды аI жәнеbI кірістері арқылы суматорға операндтар кіргізілу керек. Кідірту тізбегі тасмалдау импульсін PI+1.бір тактылық уақыт ішінде сақтайды,яғни онымен қосылатын келесі разрядтың қосындылар жұбы келгенше.Кідіртуді D-триггер орындайды.Қосу нәтижесі кіші разрядтан бастап тізбектей саналады.Операндтарды сақтау ,кіргізу үшін және
Қосындыларды жазу үшін кәдімгі ығыстыру регистрі қолдынылады. Бұл әдістің жетістілігі –аз аппараты шығындар.Жетістілігі біруақытта екі жұп қосынды қосылатындығынан –жылдам әсер етуі баяулайды.
Тізбектеп тасмалдайтын параллель сумматор сұлбасы 24,б).суреттте көрсетілген. Суматорлардың саны сандардың разрядтар санына тең.Әр сумматордың тасмалдау шығуы PI+1келесі үлкенразрядтың кірсімен жалғанады.Мұнда еш бір тасмалдау сигналы түспейді,сондықтан, кіші разрядтың тасмалдау кірісіне «0» потенциалы тұрғызылады. aI және bI қосындылары барлық разрядтары бір уақытта қосылады, ал PI тасмалдау
Алғы разрядтағы қосу амалы орындалғаннан кейін түседі. Сигнал бүкіл суматорлар тізбегі бойымен тарағанша, жоғарғы разрядтың шығысында тасмалдау сигналы қалыптаспайды. Мұндай сумматорлардың тезәсерлігі тасмалдау кедергісімен шектеледі.
Параллель тасмалдауы бар параллель сумматорлар
Параллель тасмалдауды ұйымдастыру үшін арнайы арналған түйіндер-тез тасмалдау болктары қолдынылады. Жеделдетіп тасмалдау принципін мынада: әр бір екі разрядқа қосымша екі сигнал арналған:
G—тасмалдау құружәнеH— тасмалдау таралуы.
GI = aI·bI
HI = aI + bI
GI=1болған жағдайды,яғниaI=bI=1, бұл берілген i-разрядта келесі жоғарғы разрядқаPI+1 алмасусигналы алдынғы разрядтағы функциялардың қосындысына тәуелсіз қалыптасады .
Егерде aI немесе bI «1»тең болса ,яғни HI=1 тең болса,келесі разрядқа бастапқы разрядтан алмасу сигналы болғанда ғана көшірледі.
Егерде GI=1,яғни aI=bI=1,алдынғы разрядтарға қосындылардың қалыптасуына тәуелсіз, i-разрядта келесі жоғарғы разрядқа апаратын PI+1тасмалдау сигналы қалыптастырылады.
Егерде қосындылардың біреуі aI немесеbI,«1» тең болса, яғниHI=1. Келесі разрядқа тасмалдау тек қана сигал болғанда ғана іске асырылады.
Егерде HI=HI–1=1 және PIалдынғы i-ші разрядтан алмасу сигналы болса онда көшіру i+2 разрядқа істеледі
Жалпы жағдайда үдемелі ауысу үрдісін қалыптастыру мына теңдеумен беріледі:
PI+1 = GI + HI·GI–1 + HI·HI–1·GI–2 + … + HI·HI–1·…·H2·H1·P1
Тез тасмалдау блоктары интегралдық түрде орындалған жеке микросхема немесе сумматор сұлбасымен немесе бір микросхемада арифметика-логикалық құрылғы түрде шығарылады.
7.1.3 арифметика-логикалық құрылғы
Негізгі арифметикалық амалдарға қосу және алу жатады. Алу амалдарын қосу әдісмен орындау үшін кері және қосымша кодтар жасалған. Алу амалын орындау үшін, азайтқышты қосымша кодқа өткізіп бірінші қосылғышқа қосу керек.Алынған нәтижені қосымша кодта көрсетілген. Оны сосын тікелей кодқа өткізу керек.Оң сандардың тікелей және кері кодтары бірдей.Теріс сандарды косымша кодқа айналдырғанда,барлық разрядтарын тура кодтың инверсия жасап және кіші разрядына бірді қосу керек. Қосымша кодты тікелей кодқа айналдырғанда,алынған нәтижені инверсия жасап кіші разрядқа бірдіі қосу керек
Сонымен қосу әдісімен алу амалы қосымша уақыт шығымын қажет етеді және есептеу құрлғылардың жылдамдығын азайтады.
ЭЕМ жылдамдығын өсіру үшін , арифметикалық және логикалық амалдарды түрлендірмей сандардың тікелей кодтарымен орындауды қамтамасыз ететін, құрамдастырылған арифметико-логикалық құрылғылар істелген және қолдынылады.
Қосу және алу амалдарын орындау үшін , бір разрядты арифметикалық құрылғылардың істеу әдістері 25 суретте көрсетілген.
Қосу және алу амалдарының логикалық өрнектерін салыстырғанда, қосу(25,а сурет) және алу(25,б сурет) амалдарының өрнектері бір бірне сәйкес келеді,ал қарызға алу өрнегі қосу және алу амалдарының бөлігі болып табылады.

25 сурет.Ақиқат кестсі және құрылым формулалары қосу а),алу б) және бір разрядты АЛҚ сұлбасы в).
Сонымен алу амалын орындау үшін қосымша сигналдар алудың қажетілігі жоқ,қосымша аппаратық шығымдар керек болмайды.операцияның коды сәйкес көшіру және қарызға алу сигналдарын комутациялауын қамтамасыз өткізу қажет.
25, в) суретте U кернеуінен келетін екі әр полярлы сигналмен басқару ісін орындайтын орындайтын басқару құрылғысы ролін екі клапанды қарапайым АЛҚ сұлбасы келтірілген.. 25суреттте сұлбаның бұл бөлігі пунктир сызықпен белгіленген. U=0 болғанда алу амалы орындалады, ал U=1 — қосу амалы орындалады. 25, в) суретінде
Басқару кернеуінен U әрполярлы сигналдармен басқарылатын
Көпразрядты АЛҚ интегралдық микросұлба түрінде шығарылады немесе процессордың негізі болып оның құрамына кіреді. МС 564ИП3 (26,а сурет) —бұл 16 арифметикалық және 16 логикалық операциялар жасайтын төртразрядты параллель АЛҚ

26сурет.4-разрядтыАЛУ564ИП3 сұлбасы а)564ИП4 тездетіп тасмалдау сұлбасы б).
A(а0–а3)— біріншіоперанд,
B(b0–b3)— екінші операнд,
S(s0–s3)— операция коды— 4 разрядты.
Егер M=0, онда арифметикалық амалдар орындалады: 24=16,M=1 болғанда логикалық операциялар орындалады: 24=16. Барлығы 16+16=32 операция.
F(f0–f3)—операция нәтижесі. A=B шығысында «1»пайда болады,егер азайту амалын орындағанда операцияның нәтижесі «0»тең болса , яғни A=B.
АЛҚ параллель типті болғандықтан оның G генерация шығысыжәне H тасмалдау таралуы бар. Pn және Рn+ -шығатын және кіретінтасмалдар.
Тізбектей тасмалдайтын параллель сумматордағы дай, МС АЛҚ өңдейтін сөздердің разрядтығын үлкейту үшін оны тізбектеп қосуға болады.Бұл жағдайда операция орындау уақыты өседі.Бұл уақытты азайту үшін, АЛҚ жылдам әсер етуін өсіру МС үшін, 564ИП4 жылдам тасмалдайтын сұлбаны қолдану керек. 26, б)сурет.
Төрт МС АЛҚ және бір жылдам тасмалдайтын МС 16 разядты толық параллель АЛҚалуға болады.Оның қосу уақыты бір микросұлбаның қосу уақытына тең.
Лекция.
Комбинациялық типті цифрлық құрылғылар. Екілік сумматорлар (қосқыштар). Бір разрядты сумматорлар (қосқыштар)
Көп разрядты сумматорлар (қосқыштар). Арифметикалық логикалық құрылғылар.
Комбинациялық типті цифрлық құрылғылар немесе цифрлық жадысыз автоматтар деп шығысында логикалық мәндері оның кірісіндегі сигналдар жиынтығымен,немесе олардың комбинацияларымен бір мәнді анықталатын цифрлық құрылғылар аитады.
Оларға қосқыш сұлбалар, шифраторлар және дешифраторлар мультиплексорлар және демультиплексорлар, цифрлық компараторлар. Комбинациялық типті цифрлық құрылғылар немесе интегралды микросхема процессор, жады секілді үлкен интегральды микросхемалар құрамына кіреді.
7.1Екілік сумматорлар (қосқыштар)
7.1.1 Бір разрядты сумматорлар (қосқыштар)
Цифрлық есептеуіш техникада екі және үш кірісі бар қосатын сұлбалар қолдынылады және біріншісі жартылай суматор, ал екіншісі толық бірразрядты суматор деп аталады.
Жартылай суматор тек сандардың кіші разрядтарын қосуға арналады.Толық бірразрядты суматорлардың алғашқы разрядтан келесі разрядқа көшіру үшін белгі беретін үшінші кірісі бар.
21 суретте а) жартылай суматорың ақиқат кестесі. 21 суретте б) негізгі базистің элементерімен осы кестенің негізінде МДҚП түрде жазылған құрылымдық формула.

21сурет. Бір разрядты сумматор (қосқыш): а) ақиқат кестесі, б) құрлымдық формула, в) функциональдық сұлба.
Логикалық сұлбалардың сипатайтын сапалық көрсеткіштері болып мына негізгі параметрлер саналады:жылдамәсерлігі және құрылғыцның күрделісін көрсететін элементердің саны, жылдамәсерлігіэлементердің сұлбаның элементерін өткендегі сигналдың кешігу уақытының қосындысымен анықталады.Жоғарыда көрсетілген сұлбада жылдамәсерлігі үш логикалық элементте кідіруне байланысты.
Көрсетілген сұлбаның 10 кірісі бар және 6 элементтен тұрады, яғни Кваин саны 10 тең. 21,в) суретте көрсетілген кемшілігі мынада.Оның кірісіне операндтың тура және инверісті мәндері берілу керек. Логика алгебрасының заңдарын қолдана отырып, кейбір операндтардың үстінен инверсияны алып тасатап түрлендіруге болады.Ұқшамдау реті 22,а) суретте,функциональдық сұлба-22,б) суретте, ал шартты графикалық белгісі 22,в) суретте көрсетілген.
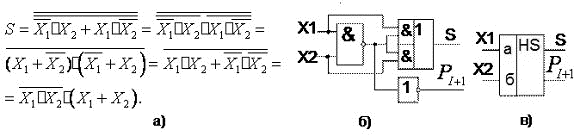
22сурет. Ұқшамдау ретіа), функциональдық сұлба, б) и шартты графикалық белгісі, в).бір разрядты жартылай сумматор.
Ықшамдалған сұлба жылдамәсерлі.Онды 6 элементің орнына 3элемент. Квайн саны 10-нан 7-ге дейін азайды.Егерде қосқыштардың саны өте көп екенін еске алсақ, ұтымның өте үлкен екенін білуге болады.
Толық бір разрядты қосындылағыштың сұлбасын екі жартылай суматордың негізінде немесе «НЕМЕСЕ» сұлбасының негізінде алуға болатынын 23,а суреттте көрсетілген.

23сурет. Бірразрядты толық сумматор: а) екі жартылай сумматор негізінде жиналған функциональдық сұлба;функциональная схема на двух полусумматорах; б) — шарты гафикалық белгісі; в) — ақиқат кесстесі: г) — ықшамдалған сұлба.
23 суреттегі функциональдық сұлбаның жұмыс істеу приципінен ақиқат кестесін толтырамыз.Осы кестені талдаудан берілген сұлбаның толық бірразрядты сумматордың функциясын атқаратынын көруге болады.Өтетін сигнал екі тізбектелген жартылай сумматор сұлбаснан және немесе сұлбасынан өткендіктен бұл сұлбаның жұмыс істеу жылдамдығы ұтымды емес.
Суматорды екі шығысы және үш кіріс бар құрылғы түрінде істеген оның істеу әркетінің мақсатына сәйкес болареді.Оның функциясының МДҚП мына түрде жазылады.

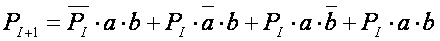
Интегралдық сұлбатехникада қолданылатын ықшамдалған мәндері:
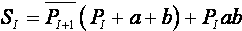
PI+1 = PIa + PIb + ab
Теңдеудің біріншісі логиканың алгебрасын қолдана отырып аналитикалық әдіспен, ал екіншісін- Карно картасының ықшамдау минимальдау әдісімен ықшамдалады. Бұл теңдеулерге сәйкес құрылған функциональдық сұлба23, г). суретінде көрсетілген. 23, а) суретіндегі сұлбаңа қарағанда жылдамырақ істейді.23, б). суретте толық бірразрядты сумматордың шарты гафикалық белгісі келтірілген.
7.1.2 Көпразрядты сумматорлар.
Көпразрядты сумматорлар жасау әдістері:
-тізбектеп қосу;
-тізбектеп тасымалдау параллель қосумен;
-параллель тасымалдау параллель қосумен.

24сурет. Көпразрядты сандарды қосу:а) -тізбектеп; б)параллель тізбектеп тасымалдаумен.
Тізбектеп қосу үшін барлық разрядтарға ортақ бір сумматор қолдынылады. 24,а сурет.
Операндтар аI және bI кірісі арқылы синхронды кіші разрядтан бастап енгізілу керек.
Кідірту тізбегі тасымалдауимпульсінің PI+1бір тактыға кететін уақыт ұзақтығындай сақтайды, яғнинымен қосылатын келесі разрядтың қосындылар жұбы келгенше.Кідіртуді D-триггер орныдайды.
Тізбектеп қосқанда, барлық разрядқа жалпы бір суматор қолдынылады.(24,а сурет) Кіші разрядтан бастап синхронды аI жәнеbI кірістері арқылы суматорға операндтар кіргізілу керек. Кідірту тізбегі тасмалдау импульсін PI+1.бір тактылық уақыт ішінде сақтайды,яғни онымен қосылатын келесі разрядтың қосындылар жұбы келгенше.Кідіртуді D-триггер орындайды.Қосу нәтижесі кіші разрядтан бастап тізбектей саналады.Операндтарды сақтау ,кіргізу үшін және
Қосындыларды жазу үшін кәдімгі ығыстыру регистрі қолдынылады. Бұл әдістің жетістілігі –аз аппараты шығындар.Жетістілігі біруақытта екі жұп қосынды қосылатындығынан –жылдам әсер етуі баяулайды.
Тізбектеп тасмалдайтын параллель сумматор сұлбасы 24,б).суреттте көрсетілген. Суматорлардың саны сандардың разрядтар санына тең.Әр сумматордың тасмалдау шығуы PI+1келесі үлкен разрядтың кірсімен жалғанады.Мұнда еш бір тасмалдау сигналы түспейді,сондықтан, кіші разрядтың тасмалдау кірісіне «0» потенциалы тұрғызылады. aI және bI қосындылары барлық разрядтары бір уақытта қосылады, ал PI тасмалдау
Алғы разрядтағы қосу амалы орындалғаннан кейін түседі. Сигнал бүкіл суматорлар тізбегі бойымен тарағанша, жоғарғы разрядтың шығысында тасмалдау сигналы қалыптаспайды. Мұндай сумматорлардың тезәсерлігі тасмалдау кедергісімен шектеледі.
Дата добавления: 2018-02-18; просмотров: 3598; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
