Кафедра системного анализа автоматики и управления на предприятии. Nbsp; Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение
Nbsp; Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Национальный минерально-сырьевой университет «Горный»
Кафедра системного анализа автоматики и управления на предприятии
Лабораторная работа № 1
По дисциплине: Современные проблемы системного анализа
Тема: «Математическое моделирование систем»
Выполнила: студентка гр. САЭ-М-12 _________ Иванова С.Г.
Проверил д.т.н., проф. ____________ Романов В.Н.
Санкт-Петербург
2012
Математическое моделирование систем.
Задача№1
1. Постановка задачи
Выход у некоторой химической реакции зависит от длительности реакции t и температуры T. Эту зависимость можно считать линейной в окрестности точки t0 = (4 + i), (в моем случае i=6, j=8, т.е. 4 + 6) ч.,
Т0= (220 + i) С, (i=6, j=8, т.е. 220 + 6). Опыты поставлены в следующих точках: t= (t0 ± 1) c.; T = (Т0 ± 10) С.
Найти: оценки параметров зависимости; оценки их дисперсий; доверительные интервалы.
2. Алгоритм решения (общие расчетные соотношения)
1) Составим матрицу инциденций;
2) Составляем: структурную матрицу F, информационную матрицу, построим дисперсионную матрицу С, транспонированную матрицу к F;
|
|
|
3) Находим дисперсионное ожидание по формуле: Sr= ∑ Δy^2;
4) Нахождение дисперсии каждого параметра.
3. Результаты расчётов
Результаты расчётов приведены ниже.
На основании исходных данных построим матрицу:
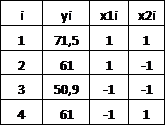
Используем множество точек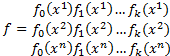 
находим структурную матрицу F:
Информационная матрица F’F представляет собой:
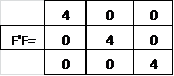
По формуле: С = (1/4)Iз, построим дисперсионную матрицу:
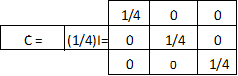
При перемножении матриц по формуле а=F*y получаем:
Рассчитаем значения функции отклика: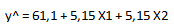 
Найдем все значения Δy , необходимо найти разницу между y1 и y^:
Необходимо найти дисперсионное ожидание, найдём его по формуле: Sr= ∑ Δy^2
Sr = 0,04
Дисперсия ошибки эксперимента: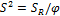 
SR/ϕ=0,004
В нашем случае число степеней свободы ϕ=N-k-1=1, получаем:
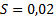
Дисперсия каждого параметра: Si=Cii*SR=1\4*0,04=0,01
Среднее квадратическое отклонение: ϕ=0,1
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Национальный минерально-сырьевой университет «Горный»
|
|
|
Кафедра системного анализа автоматики и управления на предприятии
Лабораторная работа № 2
По дисциплине: Современные проблемы системного анализа
Тема: «Определение связности и сложности систем»
Выполнила: студентка гр. САЭ-М-12 _________ Иванова С.Г.
Проверил д.т.н., проф. ____________ Романов В.Н.
Санкт-Петербург
2012
Определение сложности и связности системы
Задача№1
1. Постановка задачи
В городе имеется i+j+10 (в моем случае i=6, j=8, т.е. 6+8+10) магазинов. Покупки в k-ом магазине совершаются не менее часто чем в магазине k+j (к = 1, 2, 3 ... i).
Определить: Ранжировку магазинов по объему продаж, приняв, что ранг 1 имеет магазин с наибольшим числом продаж; долю рынка занимаемым каждым магазином; сложность и связность системы.
2. Алгоритм решения (общие расчетные соотношения)
1) Составим матрицу инциденций размером 24´24 (24 – число магазинов в городе);
|
|
|
2) Посчитаем сумму отношений в каждом столбце, чтобы определить долю рынка занимаемым каждым магазином;
Формула для определения доли рынка: ( ∑ XiYi * 100) / ∑общ.
3) Проводим ранжировку магазинов по объёмам продаж.
3. Результаты расчётов
Результаты расчётов приведены ниже в таблице.
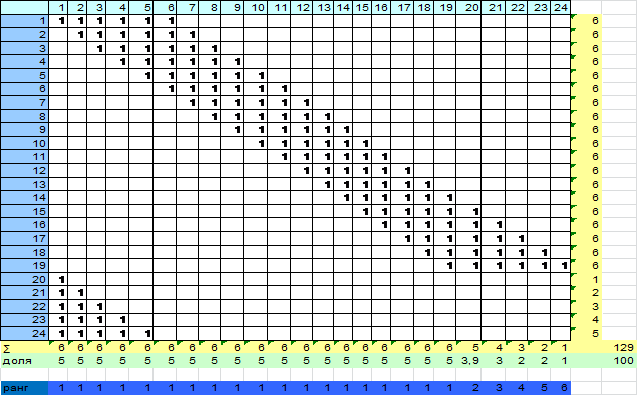
4. Анализ результатов и выводы
Проанализировав матрицу инциденций видно, что первые 19 магазинов занимают большую долю рынка, а магазин под номером 24 занимает незначительную долю рынка и значит, он неконкурентоспособен. Также первые 19 магазинов имеют самые высокие объёмы продаж, а магазин под номером 24 имеет самый низкий объём продаж.
Задача№2
1. Постановка задачи
В i+5 (в моем случае i=6, j=8, т.е. 6+5) районов города имеются i+ j+20(т.е. 6+8+20) магазинов, в которых продаётся j+10 (т.е. 8+10) ассортиментов продукции. В L районе имеется не менее L+i+j (т.е. L+6+8) магазинов, где L меняется от 1 до i+5 (т.е. 6+5). В K-ом магазине имеется не менее k + i продукции, где k =1,2,3…j.
Определить: насыщенность магазинов товарами разных групп; степень снабжения районов товарами; построить ранжировку магазинов по объему продаж, приняв, что ранг 1 имеет магазин с наибольшим числом продаж; сложность связей систем.
|
|
|
2. Алгоритм решения (общие расчетные соотношения)
1) Составляем две матрицы инциденций, первая - «Районы - магазины», состоит из 34 столбцов (34 - магазинов) и 11 строк (11 - районов), а вторая - «Магазины - ассортименты продукции», состоит из 18 столбцов (18 - ассортиментов продукции) и 34 строк (34 - магазинов);
2)Считаем сумму отношений в каждом столбце, в обеих матрицах;
3) В обеих матрицах проводим ранжировку.
3. Результаты расчётов
Результаты расчётов представлены в (матрице 1 и матрице 2) ниже в таблицах.
Матрица 1 - «Районы - магазины»
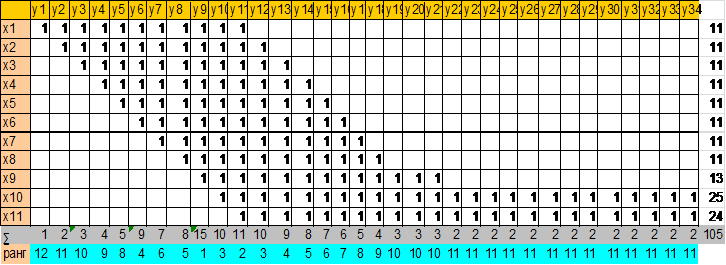
Подсчёт размерности симплексов и числа комплексов, определение первого структурного вектора комплекса и эксцентриситета у каждого симплекса, определение вектора препятствий.
q max = 25
q=24, Q=1 {X10};
q=23, Q=1 {X10,Х11};
.
.
q=13, Q=1 {X10,Х11};
q=12, Q=2 {X9},{X10, Х11};
q=11, Q=1 {X9, X10, Х11};
q=10, Q=9 {X1},{ X2},{ X3},{ X4},{ X5},{ X6},{ X7},{ X8},{X9, X10, Х11};
q=9, Q=5 {X1,X2},{ X3,X4},{ X5,X6},{ X7,X8},{X9, X10, Х11};
q=8, Q=4 {X1,X2,X3},{,X4,X5,X6},{ X7,X8,X9, X10 },{ Х11};
q=7, Q=3 {X1,X2,X3,X4 },{X5,X6, X7,X8},{X9,X10,Х11};
q=6, Q=3 {X1,X2,X3,X4 ,X5},{X6, X7,X8,X9,X10},{ Х11};
q=5, Q=2 {X1,X2,X3,X4 ,X5,X6 },{ X7,X8,X9,X10,Х11};
q=4, Q=2 {X1,X2,X3,X4 ,X5,X6, X7 },{ X8,X9,X10,Х11};
q=3, Q=2 {X1,X2,X3,X4 ,X5,X6, X7, X8},{X9,X10,Х11};
q=2, Q=2 {X1,X2,X3,X4 ,X5,X6, X7, X8, X9},{X10,Х11};
q=1, Q=2 {X1,X2,X3,X4 ,X5,X6, X7, X8, X9, X10},{Х11};
q=0, Q=1 {X1,X2,X3,X4 ,X5,X6, X7, X8, X9, X10,Х11}.
Q = (1111111111112195433222221)
E(X1) = 10-9/9+1 = 1/10;
.
.
.
E(X8) = 10-9/9+1 = 1/10;
E(X9) = 12-11/11+1 = 1/12;
E(X10) = 24-23/23+1 = 1/24;
E(X11) = 23-23/23+1 = 0.
D = (0000000000001084322111110)
Комплекс сильно связан при всех размерностях, кроме (q=12, q=10, q=9, q=8, q=7, q=6, q=5, q=4, q=3, q=2, q=1). Все симплексы наибольше интегрированы в комплексе, кроме Х11. Следовательно магазин Х10 более насыщен товарами разных групп.
Матрица 2 - «Магазины - ассортименты продукции»
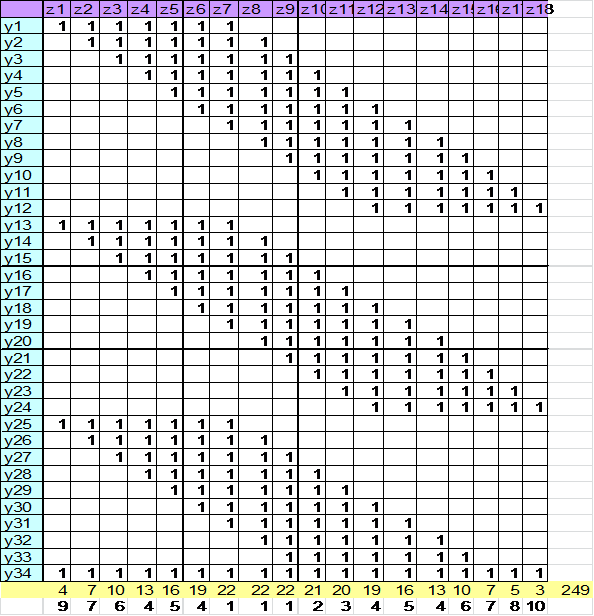
Подсчёт размерности симплексов и числа комплексов, определение первого структурного вектора комплекса и эксцентриситета у каждого симплекса, определение вектора препятствий.
q max = 17, Q=1 {y34};
q=16, Q=1 { y34};
q=15, Q=1 { y34};
q=14, Q=1 { y34};
q=13, Q=1 { y34};
q=12, Q=1 {y33,y34};
q=11, Q=1 {y33,y34};
q=10, Q=1 {y33,y34};
q=9, Q=1 {y33,y34};
q=8, Q=1 {y1,…,y34};
q=7, Q=1 {y1,…,y34};
q=6, Q=1 {y1,…,y34};
q=5, Q=1 {y1,…,y34};
q=4, Q=1 {y1,…,y34};
q=3, Q=1 {y1,…,y34};
q=2, Q=1 {y1,…,y34};
q=1, Q=1 {y1,…,y34};
q=0, Q=1 {y1,…,y34}.
Q = (1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)
E(y1) = 6-6/6+1 = 0;
.
.
E(y33) = 6-6/6+1 = 0;
E(y34) = 17-12/12+1 = 5/13
D = (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
Комплекс сильно связан при всех размерностях (от q=17 до q=0). Симплекс y34 наибольше интегрирован в комплексе. Следовательно магазин y34 более насыщен товарами разных групп.
4. Анализ результатов и выводы
По результатам решений было выявлено, что район x10 лучше всех снабжается товарами, а магазин y34 более насыщен товарами разных групп.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Национальный минерально-сырьевой университет «Горный»
Кафедра системного анализа автоматики и управления на предприятии
Лабораторная работа № 3
По дисциплине: Современные проблемы системного анализа
Тема: «Определение устойчивости, адаптивности линейных систем»
Выполнила: студентка гр. САЭ-М-12 _________ Иванова С.Г.
Проверил д.т.н., проф. ____________ Романов В.Н.
Санкт-Петербург
2012
Определение устойчивости, адаптивности линейных систем
Задача№1
1. Постановка задачи
Дано дифференциальное уравнение, которым описывается система, следующего вида:
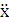+(b-i) 
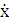+(c-j)x=0, (1.1)
где i=6,а j=8 (i и j последние две цифры шифра студента).
Необходимо проверить, будет ли система устойчивой при b=3 и c=4.
2.Алгоритм решения (общие расчетные соотношения)
Составим матрицу, используя критерий Рауса-Гурвица, для того, чтобы определить устойчивость системы, задаваемой дифференциальным уравнением (1.1). Имея ввиду, что a0 - коэффициент при старшей производной, a1 - коэффициент при первой производной, a2 - коэффициент при x, a3 - коэффициент при свободном члене.
3.Результаты расчётов
Окончательный вид уравнения (1.1) (с своими значениями):
х ̈+(-3)х ̇+(-4)x=0. (1.2)
Матрица:
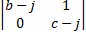А= 
, А= 
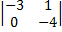, где ao = 1, a1 = -3, a2 = -4, a3 = 0.
Проверка устойчивости системы
Условия устойчивости:
b-i >0, -3<0;
c-j >0, -4<0;
(b-i)(c-j)>0 12>0.
4. Анализ результатов и выводы
Система устойчива при следующих условиях: b-i›0, c-j›0, (b-c)(c-j)›0.
Система с данными b=3, с=4 устойчива т.к. (3-6)(4-9)›0
Задача 2
1. Постановка задачи
Определить по приведенному графику является устойчивой система.
2.Алгоритм решения (общие расчетные соотношения)
1) Составим матрицу взаимосвязей, начиная с вершины U1. В соответствующую ячейку матрицы ставится (+1), если стрелка направлена из первого элемента во второй, и стоит знак (+) ; ставится (-1), если стрелка направлена из первого элемента во второй, и стоит знак (-). (0) ставится, если стрелки отсутствуют.
2)Составим характеристическое уравнение матрицы. Система считается не устойчивой, если наибольший по модулю корень характеристического уравнения больше единицы. 1-цы.
3. Результаты расчетов
Матрица1 (для графа 1)
| U1 | U2 | U3 | U4 | |
| U1 | 0 | 1 | -1 | 0 |
| U2 | 0 | 0 | 0 | 1 |
| U3 | 0 | 0 | 0 | 1 |
| U4 | 0 | 0 | 0 | 0 |
Матрица2 (для графа2)
| P1 | H1 | W | I | G | H2 | P2 | |
| P1 | -1 | 1 | 0 | 0 | 0 | 0 | 0 |
| H1 | -1 | 0 | 1 | 1 | 0 | 0 | 0 |
| W | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| I | 0 | -1 | -1 | -1 | 0 | 0 | 0 |
| G | 0 | -1 | 0 | 0 | 0 | -1 | 0 |
| H2 | 0 | 0 | 0 | 1 | 0 | 0 | -1 |
| P2 | 0 | 0 | 0 | 0 | 0 | 1 | -1 |
Для процесса распространения возмущения в системе, начинающегося в вершине U1 , можно записать выражение для значения возмущения j в момент времени t : Vj(t)=Vj(0)+[I+A+A2+...+At], для второй матрицы также. Пусть t=2, а Vj(0)=0, тогда получится выражение для первой матрицы : Vj(2)=0+[I+A+A2], где I - единичная матрица, А - наша матрица, а А2 - наша матрица в квадрате. И проведя подсчёты, получается, что Vj(2)=0. Из этого следует, что возмущение в момент времени t=2 отсутствует. Запишем характеристическое уравнение (А-λЕ=0) для матрицы 1: λ4-2λ=0 и найдём для него корни, получается λ1=0, λ1,2,3=1,2, так как три корня >1, то от сюда следует, что система является неустойчивой.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Национальный минерально-сырьевой университет «Горный»
Дата добавления: 2018-02-18; просмотров: 357; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!