Свойства топографической карты
Топографические карты - это подробные общегеографические карты, отображающие в первую очередь главную особенность формы Земли - рельеф местности, а также размещение и свойства природных и социально-экономических объектов местности. Топографические карты подразделяются на карты суши и карты шельфа и внутренних водоёмов. На топографических картах суши с большей или меньшей детальностью и точностью, допускаемой масштабом, изображаются рельеф, гидрография, растительный покров, населённые пункты, пути сообщения и другие объекты.
Топографические карты шельфа охватывают выровненную часть подводной окраины материков, прилегающих к берегам суши и имеющую с ней общее геологическое строение.
Топографические карты суши и шельфа используются при решении широкого круга задач в хозяйственной, научной и оборонной областях.
Во многих случаях топографические карты служат основным источником информации о местности. Полевые физико-географические, геологические, геоботанические и другие исследования природной среды, так же как и социально- и экономико-географические изыскания дают лучшие результаты при всестороннем использовании топографических карт.
Топографические карты широко применяются при проектировании и строительстве населённых пунктов, промышленных, энергетических и гидротехнических сооружений, путей сообщения, при мелиорации (осушение и орошение земель, регулирование стока вод и др.). Они необходимы при земле- и лесоустроительных работах, а также для ведения сельского хозяйства: составление земельного кадастра и др.
|
|
|
Топографическая карта и картографическое изображение на ней - самая целесообразная форма представления информации для создания географических информационных систем (ГИС).
Лист топографической карты включает картографическое изображение (совокупность сведений о местности), отображаемое условными знаками и построенное на математической основе и вспомогательное оснащение. Элементами оснащения карты являются: условные знаки (легенда), название карты, обозначение её масштаба, изображение линий картографической сетки и др.
Масштаб. Измерение длин линий на карте
Понятие о масштабе нами дано (§1), а теперь более подробно.
Масштаб указывается под южной рамкой листа карты. Масштабы бывают: численный, именованный, линейный и поперечный.
Численный масштаб выражается дробью, у которой числитель единица, а в знаменателе - число, показывающее во сколько раз линия местности (проекция) уменьшена. Численный масштаб записывается, например, так: 1/10000 или 1:10000.
Чем больше знаменатель, тем больше уменьшение длин, тем мельче изображение объектов на карте, т.е. мельче масштаб карты.
|
|
|
Именованный масштаб – словесное пояснение соотношений длин линий на карте и на местности. Например, численный масштаб карты 1:25000; именованный: «в одном сантиметре 250 метров».
Линейный масштаб изображается в виде линий (рис.1 в приложении 1), разделённых на 2х или 1 см отрезки (основания масштаба); левый крайний отрезок от нуля делится на 20(10) частей. Отрезки вправо от нуля подписываются применительно к масштабу. Линейный масштаб позволяет определять с помощью измерителя значительно точнее длину линии на местности, не производя математических расчётов, как это делается при численном масштабе.
 |
Измерение длины линии на карте с помощью измерителя и линейного масштаба производится следующим образом. Ножки измерителя устанавливают в точках, обозначающих концы данной линии, при этом угол между плоскостью карты и каждой ножкой измерителя должен быть не менее 60˚. Не изменяя раствора,
Рис.4.
измеритель переносят на линейный масштаб так, чтобы правая ножка расположилась на оцифрованном отрезке, а левая – на дробном основании.
На рис. 4 представлен случай, когда измеренная длина линии равна 380 м. Для контроля линия измеряется дважды. Расхождение между результатами измерений не должно превышать двойной точности масштаба (2t), вычисляемой по формуле
|
|
|
t=0,02• М, (3)
где 0,02 см – минимальная ошибка при измерении линии измерителем (толщина иглы); М – знаменатель масштаба карты.
Линию, длиннее линейного масштаба, измеряют по частям раствором измерителя, кратным длине линейного масштаба. В этом случае разность (Δd) между результатами измерений линии в прямом и обратном направлениях не должна быть больше:
Δd= 2t√n, (4)
где n – число установок измерителя при измерении заданной линии.
 |
Поперечный масштаб. Для повышения точности измерения расстояний применяют поперечный масштаб, который строится в виде параллельных равноотстоящих прямых, разделённых так же, как и линейный масштаб на равные отрезки (рис. 5а). Длина основания (q) чаще всего бывает 2 см.
Рис.5.
Крайняя левая часть масштаба по линиям МО и NВ делится обычно на 10 равных частей (дробная часть основания), а точки деления соединяются наклонными линиями (трансверсалями). В результате такого построения отрезки прямых между перпендикуляром ОВ и первой трансверсалью будут различной длины. Самый малый из них а1b1=q′ является наименьшим делением поперечного масштаба (рис. 5 б). Его величину можно определить на основании свойства подобных треугольников. Количество делений на перпендикулярах ОВ равно 10. Следовательно, отрезок Оb1, оставляют 1⁄ 10 перпендикуляра ОВ. Учитывая, что треугольники ОАВ и Оa1b1 подобны, тогда а1b1=0.1 АВ. Из этого же условия a2 b2 = 0,2 АВ и т.д. А так как АВ= 0,1q то a1b1 = 0,01q
|
|
|
Длину измеряемого с помощью поперечного масштаба отрезка (d) можно определить по такому выражению (рис. 5в)
d= (n•q+m•0,1•q+k•0,01•q) •M, (5)
где n – количество целых оснований (q);
m – количество полных десятых долей основания (q);
k – количество сотых делений основания (q);
М – знаменатель масштаба;
q – основание поперечного масштаба (1 или 2 см).
Применительно к длине отрезка, обозначенного раствором измерителя, (положение I), если принять масштаб 1:50000 будем иметь: q = 2 см; M = 500 м; n = 1; m = 4; k = 5;
d= (1•2+4•0,1•2+5•0,01•2) •500 = 1450 м.
На практике все получается значительно проще. Измеритель, с установленным по карте раствором, переносят на нижнюю линию масштаба так, чтобы одна его игла совместилась с одним из перпендикуляров справа от нулевой отметки, а другая оказалась в пределах крайнего левого основания (рис. 5в, положение I), затем измеритель перемещают вверх до тех пор, пока левая игла не совпадет с пересечением одной из наклонных линий с горизонтальной прямой (положение II), при этом обе иглы должны быть на одной горизонтальной прямой. Теперь достаточно подсчитать количество оснований (q) – оно равно единице; количество десятых долей основания (0,1q), оно равно 4; и количество сотых долей основания (0,01q) оно равно 5 и вычислить длину. Например, применительно к численному масштабу 1:50000 основание масштаба (q) равно 2 см, а в масштабе это 1000 м, одно деление дробного основания – 100 метров (в положении II таких 4 деления) плюс 400 м; ножки измерителя находятся на 5 линии, плюс отрезок 5•10=50 м. Таким образом, полная длина отрезка равна 1000 м + 400 м + 50 м = 1450 м.
Аналогично определяются длина линии, выделенной жирным тоном, на поперечном масштабе (рис. 5в). Её длина равна 2•1000 м + 4 • 100 + 7•10 м = 2470 м.
Выполняя расчетно-графическую работу (приложение 1), студенты вычерчивают линейный и поперечный масштабы и подписывают их применительно к численным (задаваемых преподавателем). Для закрепления навыков и знаний в работе с масштабами каждый студент изображает в табл. 1 (приложение 1) три отрезка разной длины, производит измерение их длин в трех масштабах, а результат записывает в табл.1 приложения.
При измерении длины линий по карте надо помнить, что мы находим горизонтальные проекции их (ф2), а не истинные значения (наклонные длины).
Связь между ними такова (рис. 6)
 |
Рис. 6.
d=D•cos ν (6)
h=HB-HA (7)
tgν= h/d (8)
ν=arctg h/d (9)
D=d/cosν (10)
где D – наклонная длина линии на местности (измеряется лентой при съемках);
ν – угол наклона местности (линии) к горизонту (измеряется теодолитом при съемках);
HA,HB – высоты точек A и B над уровнем Балтийского моря (определяются по карте);
d – горизонтальная проекция (линия A′B′) линии AB.
Работая с картой, горизонтальную проекцию (d) линии местности вычисляют по формуле 2, затем вычисляют ее наклонную длину (D) по формуле 10, если будет известен угол наклона (ν).
Угол наклона (крутизна ската) можно определить по формуле 9, если местность имеет прямолинейный характер изменения, или вычислить, если местность неровная, как среднеарифметическое по графику «Масштаб заложений», изображенному на карте (рис.7)
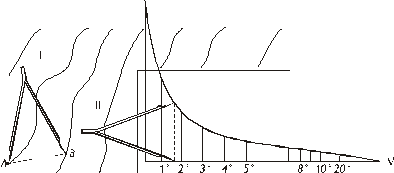 |
Рис. 7
График "Масштаб заложений" для углов наклона строится по формуле.
d=h0/tgν, (11)
где h0 – высота сечения рельефа (указывается под линейным масштабом карты), величина постоянная для данной карты;
ν – угол наклона; ему придаются значения: 1˚, 2˚, 3˚ … 10˚.
Подставляя значение h0 и νi в формулу 11, получают d1, d2 , d3 ….. Затем проводят горизонтальную линию (ось ν), на ней откладывают равные отрезки, соответствующие 1˚, 2˚, 3˚ … 10˚; в точках 1, 2, 3 откладывают в масштабе карты перпендикуляры: d1, d2, d3 ….. концы ординат соединяют кривой линией, получая график «Масштаб заложений» (рис. 7).
Следует помнить, что с помощью такого графика можно определить угол наклона (крутизну) только между двумя ближайшими горизонталями (с разными отметками, превышение между которыми равно h0 карты).
Пример. Пусть требуется определить крутизну рельефа между точками А и В (рис. 7). Устанавливают ножки измерителя в точках А и В, переносят раствор измерителя на график, таким образом, чтобы одна игла установилась на оси ν в точке 1, другая игла располагается в сторону кривой, затем перемещают измеритель по оси ν параллельно ординатам графика до тех пор, пока другая точка (игла) не попадет на кривую. Эту точку проектируют на ось ν (там находится игла измерителя) и на глаз оценивают положение точки между двумя градусными делениями. На рис. 7 ν = 1˚ 40΄ (приблизительно).
Если линия на карте пересекает несколько горизонталей, то углы наклона между другими (последующими) точками находятся аналогично, а средний угол наклона линии к горизонту вычисляется:
νср = (ν1 + ν2 + … + νn)/n. (12)
Для закрепления знаний по определению углов наклона линии на карте и по установлению зависимости между наклонной длиной линии и ее горизонтальной проекцией студенты приводят в расчетно-графической работе (приложение 1) рисунок (3) и формулы.
Условные знаки
Картографическими условными знаками называют применяемые на картах обозначения различных объектов и их характеристик. Условные знаки и их системы образуют особый искусственный язык – язык картографии. Они передают содержание карт, т.е. знания о реальной действительности, заключённые в картах. Картографические знаки обозначают предметы, явления, процессы (нефтяная вышка, линия электропередачи, болото, населённый пункт, рельеф местности, температура воздуха, морские течения и т.д. и т.п.).
Для пользования картой необходимо усвоить значение картографических знаков, их смысловое содержание, т.е. отношение к изображаемым предметам, явлениям и процессам.
Совокупности знаков выполняют на картах более широкие функции. Они показывают сочетания и взаимосвязи объектов, формируют пространственный образ явлений, позволяют устанавливать закономерности их размещения и таким образом дают новые знания сверх суммы информации, заложенной в отдельных условных знаках карты.
 |
Условные знаки подразделяются на масштабные, внемасштабные и линейные (рис.8).
Рис. 8.
Масштабными условными знаками изображаются объекты, горизонтальные размеры которых могут быть выражены в масштабе карты.
Внемасштабными (или точечными) условными знаками называют на картах объекты, занимающие на местности очень небольшую площадь, не выражающуюся в масштабе карты, положение которых фиксируется на картах точкой. Рисунок знака имеет или правильную геометрическую форму (кружок, треугольник и т.п.) или схематически, упрощённо воспроизводит внешний вид объекта. Истинное положение объекта на местности определяется одной из точек знака, которая находится: в центре знаков геометрической формы (1, 2 рис. 8), в середине основания у фигур неправильной формы (6 рис. 8); в вершине прямого угла у основания знаков с «подсечкой» (3 рис. 8).
Линейные знаки применяются для изображения на картах предметов местности, которые имеют значительную протяжённость при сравнительно малой ширине, не выражающейся в масштабе карты (пути сообщения, линии связи, границы и т.п.). Линейный знак (9, 10 рис. 8) передаёт расположение объекта на местности с преувеличением его ширины (в масштабе карты), при этом ось знака совпадает с положением на местности оси объекта.
Для дополнительной характеристики применяются пояснительные условные знаки:
а) собственные названия населённых пунктов, рек и др;
б) сокращённые надписи, перечень которых даётся в таблицах условных знаков (характер производства, материал сооружений и покрытия дорог и др.);
в) числовые показатели (длина, ширина и грузоподъёмность мостов; высота и толщина деревьев в лесу; ширина и глубина рек и др.).
г) знаки (порода деревьев в лесу, коллейность железных дорог, направление течения рек и др.).
Для закрепления знаний по изучению условных знаков, а также для приобретения навыков в черчении, студенты вычерчивают несколько условных знаков (рис. 4 в приложении 1).
§6. Определение географических и прямоугольных координат.
Особенностью топографических карт является наличие на них двух систем координат (исходя из сущности поперечно-цилиндрической проекции Гаусса-Крюгера): географической и прямоугольной, что позволяет определять как географические, так и прямоугольные координаты любой точки.
Географическая система координат обозначена на карте граничными линиями: западным и восточным меридианами, южной и северной параллелями.
 |
Рабочее поле карты заполнено сеткой линий, образующих квадраты прямоугольной системы координат (рис. 9).
Рис. 9.
Эти линии называются линиями километровой сетки, т.к. они проведены через 1 км, в масштабе карты: горизонтальные – параллельно экватору, вертикальные – параллельно осевому меридиану зоны. Вертикальная линия означает ось X, горизонтальная – ось Y.
1. Определение географических координат точки
 |
Для определения широты φА точки А (рис.10)
Рис. 10.
проводят через эту точку параллель (т.е. линию, параллельную южной стороне рамки карты). Находят расстояние от этой параллели до южной стороны рамки, оценивая секунды на глаз (37″). Так как широта южной рамки равна 54˚40′, то искомая широта точки А получится φА =54˚40΄37″.
Долготу точки А находят аналогично, проведя через точку А истинный меридиан. Для данного примера λА=18˚00΄32″.
 |
2. Определение прямоугольных координат точки
Рис. 11.
Приняв за оси координат линии километровой сетки (X=6601, Y=9.704), опускают на них из определяемой точки перпендикуляры ∆х и ∆y (рис.11), длины которых измеряют с помощью поперечного масштаба. Для данного примера:
XВ=6601000 м + ∆x = 6601550 м
YВ=9704000м + ∆y = 9704415 м
Для закрепления знаний студенты определяют координаты двух точек, задаваемых индивидуально, а результаты записывают в таблицу 2 приложения 1.
Ориентирование линии
Под ориентированием линии на местности (карте) понимается ее положение относительно северного направления меридиана, т.е. угол между северным направлением меридиана и направлением данной линии. В качестве углов, определяющих положение линии, служат: азимут, дирекционный угол и румб. Исходными направлениями в геодезии приняты: истинный (географический) меридиан, осевой меридиан зоны и магнитный меридиан.
 |
Истинным азимутом линии в данной точке ее называется горизонтальный угол между северным направлением истинного меридиана в этой точке и направлением линии. Этот угол отсчитывается по ходу часовой стрелки. Истинный азимут обозначается буквой А и изменяется от 0 до 360˚ (рис.12)
Рис. 12.
Азимут прямого направления P1P2 называется прямым, а обратного (P2P1) направления – обратным азимутом. Прямой азимут направления P1P2 (рис. 12) будет А1 , а обратный для того же направления – А2. Так как меридианы не параллельны между собой, а пересекаются в точке полюса (Pn), то азимут линии в каждой точке ее имеет разное значение. Угол между направлениями двух меридианов в данных двух точках (P1 и P2) называется сближением (γ) меридианов. Как видно из рис. 12, зависимость между прямым и обратным азимутом выражается формулой:
А2=А1+180+γ. (13)
На практике иногда вместо азимутов пользуются румбами. Румбом называется острый угол между северным или южным (ближайшим) направлением меридиана и направлением на точку. Румбы обозначаются буквой r с индексами, указывающими четверть, в которой находится линия.
Например: rЮВ – линия находится в юго-восточной четверти (рис. 13). Связь между румбами и азимутами приведена в таб. 1
Таблица 1
| Азимуты | Румбы | Четверть; названия |
| 0-90˚ | r1=A1 | 1 – СВ |
| 90-180˚ | r2=180˚-A2 | 2 – ЮВ |
| 180-270˚ | r3=A3-180˚ | 3 – ЮЗ |
| 270-360˚ | r4=360˚-A4 | 4 – СЗ |
Дирекционным углом линии на плоскости называется угол между северным направлением осевого меридиана и направлением (P1P2) на данный предмет (точку). Дирекционные углы измеряются транспортиром также как и азимуты и изменяются так же как и азимуты; обозначаются буквой α.
Как следует из рис. 14, связь между азимутом и дирекционным углом выражается формулой:
А=α+γ, (14)
где γ – сближение меридианов в т. P1
 |
Рис. 13
 |
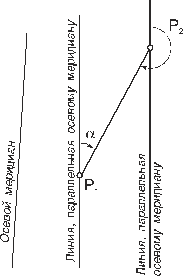 |
Рис. 14 Рис. 15
Прямой и обратный дирекционные углы одной и той же линии отличаются на 180˚ (рис.15)
Магнитные азимуты. При решении ряда практических задач целесообразно пользоваться магнитными азимутами, т.к. они легко определяются с помощью простых приборов, таких как компас, буссоль, главной частью которых является магнитная стрелка.
Магнитные азимуты (АМ) отсчитываются так же, как и истинные азимуты, – по ходу часовой стрелки от 0 до 360˚, но от направления магнитного меридиана.
Зависимость между магнитным азимутом и истинным азимутом такова:
А=АМ+δ. (15)
Здесь δ – склонение магнитной стрелки (указывается на карте).
Связь между дирекционным углом и магнитным азимутом определяется из решения двух равенств (ф. 14 и 15), у которых левые части равны, а значит, будут равны и правые, т.е.
α+γ=АМ+δ
α=АМ+δ-γ. (16)
Здесь γ и δ с учетом своих знаков.
Для закрепления теоретических знаний студенты измеряют элементы ориентирования линии АВ, заданной преподавателем (табл.2 приложении 1), вычисляют магнитный азимут её и измеряют длину линии АВ. Результаты измерений и расчетов заносят в табл. 3 расчетно-графической работы (приложение 5).
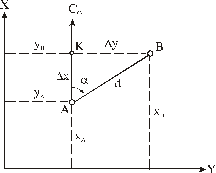 |
При определении координат, измерении длин линий и элементов ориентирования с помощью транспортира возможны ошибки. Чтобы избежать появления грубых ошибок, все измерения должны производиться дважды. Одним из косвенных способов контроля измерений является решение обратной геодезической задачи, сущность которой заключается в определении дирекционного угла (α) и горизонтального проложения (d) линии по известным координатам её концов (рис.16).
Рис. 16.
Обратная геодезическая задача.
Дано: ХА YА; ХВ YВ. Определить α и d.
В прямоугольном треугольнике АКВ (рис.16) имеем: КВ=∆y= =YB-YА; АК=∆x =ХВ-ХА. Далее запишем
tgαAB= (YB-YA)/(XB-XA)=∆y AB/ ∆xAB (17)
αAB=acrtg (∆yAB/∆xAB) (18)
dAB=(∆yAB/sinαAB) (19)
dAB=(∆x /cosαAB) (20)
По формуле 18 фактически вычисляется румб (острый угол) линии. Положение линии (четверть) находится в зависимости от знаков у приращений координат (∆x и ∆y), которые определяются по табл. 2.
Таблица 2
| Четверть, Название румба | Знак у приращения координат | |
| ∆x | ∆y | |
| I СВ | + | + |
| II ЮВ | − | + |
| III ЮЗ | − | − |
| IV СЗ | + | − |
Определив четверть, в которой находится искомая линия АВ по зависимости между румбом и дирекционным углом (табл.1), вычисляют её дирекционный угол.
Решение обратной геодезической задачи целесообразно выполнять по формуляру (табл. 4 в приложении 1). Контролем правильности расчётов является: dAB, вычисленное по формуле 19 и dАВ, вычисленное по формуле 20 должны быть одинаковыми или отличаться не более чем на 2 см.
По определённым координатам точек А и В (табл. 2 в приложении 1.) студенты вычисляют расстояние между точками и дирекционный угол линии (табл. 4 в приложении 1), сравнивают вычисленные значения (αAB и βАВ) с измеренными (табл. 3 в приложения 1) и составляют табл. 5 в приложении 1. Если расхождение в длине линии составляет не более 1 мм (в масштабе карты), а расхождение в дирекционном угле не более одного градуса (для школьного транспортира), можно считать, что прямоугольные координаты точек А и В определены удовлетворительно. В противном случае координаты точек А и В определяются заново.
Оценка точности произведённых измерений в расчётно-графической работе заключается в сравнении результатов (табл. 5 в приложении 1.).
Определение отметок
На топографических картах рельеф местности изображается горизонталями. Горизонталь − это плавная замкнутая кривая линия, соединяющая на карте (плане) точки с одинаковыми отметками. Горизонтали подписываются кратно принятому сечению (h0). Подписывается, как правило, каждая пятая горизонталь, которая изображается утолщённой.
Из формулировки горизонтали можно заключить, что отметка точки, лежащей на горизонтали будет равна отметке этой горизонтали. Пусть требуется определить отметку точки С, расположенной между смежными горизонталями с отметками Н1 и Н2 (рис. 17).
 |
Рис. 17.
Проводят через точку С прямую, нормальную к горизонталям (кратчайшее расстояние) и измеряют в миллиметрах отрезки d0 и е. Искомая отметка, как видно из разреза (рис.17), равна:
НС= Н1+ ∆h (21)
где ∆h − превышение точки С над точкой 1.
Из подобия треугольников 1К2 и 1LC можно записать:
∆h/h0=e/d0 (22)
∆h=(e/d0)h0
где h0 − высота сечения рельефа или разность отметок горизонталей в точках 1 и 2.
Подставив вычисленное значение ∆h (ф. 22) в формулу 21, получают отметку точки С.
Отметки таких точек приходится вычислять, как правило, при построении профиля местности по заданному направлению.
Построение профиля
Профиль местности − это вертикальный разрез рельефа местности, построенный в двух масштабах: горизонтальном и вертикальном.
Построение профилей по картам необходимо при разнообразных исследованиях природных условий территории для решения научных и практических задач. Например, с помощью профиля можно установить, имеется ли взаимная видимость между двумя точками местности. Построением профилей по ряду направлений, исходящих из данной точки, можно нанести на карту участки местности, невидимые с этой точки (так называемые поля невидимости) и др.

Пусть требуется построить профиль местности на карте масштаба 1:10000 по линии ВD (рис. 18а)
а) б)
Рис. 18
Точки пересечения линии BD с горизонталями нумеруют; фиксируют на карте по линии BD точки перегиба местности (характерные точки), присваивая им номера (3а, 6а) и вычисляя их отметки как и т. В аналитически (§ 8).
На листе миллиметровой бумаги строят графы расстояний и отметок (рис.18б). В графу расстояний в масштабе карты (измерителем, по линейному масштабу) переносят длины соответствующих интервалов (расстояние между точками пересечения линии ВD со всеми горизонталями, а также с характерными линиями рельефа − тальвегом и водоразделом). В графу отметок записывают высоты соответствующих точек (В,1,2...9,10 D). Над всеми перенесёнными точками от линии условного горизонта восстанавливают перпендикуляры и на них в масштабе (в 10 и более раз крупнее горизонтального) откладывают отрезки, равные разности отметки точки и отметки условного горизонта.
Концы перпендикуляров соединяют плавной кривой линией.
Студенты, выполняя расчётно-графическую работу, строят профиль по линии АВ (обозначенной ранее), составляя при этом таблицу 6 (приложение 1) с элементами линии: заложением, превышением (сечением), уклоном и др. В расчётно-графической работе они иллюстрируют пример определения отметки точки аналитическим способом.
 |
В таблице 6 (приложение 1) превышения (h0) находятся как разность отметок в точках А,1,2…; заложения (d0) находится с помощью измерителя и линейного масштаба; уклон вычисляется по формуле (рис.19):
Рис.19
i=h0 / d0 (23)
здесь h0 − высота сечения рельефа;
d0 – заложение горизонталей.
В общем виде уклон линии находится по выражению:
i= h/d (23')
здесь h − превышение одной точки над другой;
d − горизонтальная проекция между точками.
Угол наклона находится по формуле 9(23) или по графику «Масштаб заложений».
Наклонная длина (D) находится по формуле (рис. 19):
D=√h02+d02 (24)
В общем виде по формуле
D=√h2+d2 (24΄)
Измерение площадей
Площадь участков местности требуется знать для решения многих инженерно-технических и планово-экономических задач. Измерения площадей участков местности по топографическим картам (планам) производится графическим, аналитическим и механическим способами.
При измерении площади участка по карте находится его проекция (s) на горизонтальную плоскость, а для нахождения фактической площади на физической поверхности Земли (S) необходимо ее вычислить по формуле:
S = s/cosνср, (25)
где νср – средний угол наклона площади участка Земли по отношению к горизонтальной плоскости (плоскости проекции).
 |
Рассмотрим сущность графического способа. Если участок Земли, изображенный на карте, имеет форму многоугольника, то его площадь разбивают на простые геометрические фигуры (рис. 20) – треугольники, квадраты и определяют площадь каждой, а окончательную площадь находят как сумму площадей простых фигур.
Рис. 20
Измерение площадей участков, имеющих сложную, неправильную конфигурацию, чаще производят с помощью палеток и планиметров, что дает наиболее точные результаты.
 |
Сеточная палетка (рис.21) представляют собой прозрачную пластину (из пластика, органического стекла или кальки) с награвированной или начерченной сеткой квадратов.
Рис. 21
Палетку накладывают на измеряемый участок и по ней подсчитывают количество полных квадратов (N) и количество неполных квадратов (n) по контуру фигуры. Считая, что из двух неполных квадратов образуется один полный (ввиду малых размеров квадрата), общее количество полных квадратов по всей фигуре будет:
N+n/2
Дата добавления: 2018-02-15; просмотров: 2461; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
