Схема та принцип роботи однофазного мостового випрямляча

 

   Схема випрямляча складається з силового трансформатора і моста із чотирьох діодів VD1 –VD4 (рис. 1.5). Принцип роботи мостового випрямляча розглянемо за умови його роботи на чисто активне навантаження.

   Діоди VD1 і VD2 відкриті під час додатньої півхвилі напруги u₂ (на рис. 1.5 полярність u₂ показана без дужок) і ця півхвиля напруги u₂ формує в цей же час напругу навантаження u_d.

   Під час від’ємної півхвилі напруги u ₂ (на рис. 1.5  полярність u₂ показана в дужках) відкриті діоди VD3 і VD4, через які напруга u₂ прикладається до навантаження з тією ж полярністю, що і в попередньому випадку.

   Випрямлена напруга u_d за умови роботи випрямляча на чисто активне навантаження має вигляд однополярних півхвиль напруги u₂ (див. рис. 1.6, а). В силу ідентичності кривих u_d для розглянутих випрямлячів ( мостового та з виводом нульової точки вторинної обмотки трансформатора) отримане співвідношення (1.2) справедливе і для мостової схеми випрямлення.

   Оскільки струм I_d=U_d/R_d   розподіляється порівну між парами діодів

(рис. 1.6, б), то струм І_а кожного діода в досліджуваній схемі також рівний I_d/2.

    Зворотна напруга прикладена одночасно до двох закритих діодів на проміжку провідності інших і створюється напругою вторинної обмотки трансформатора u₂ (рис. 1.6, д). Максимальна зворотна напруга визначається амплітудним значенням напруги u₂

                             U_{a макс}=                                      (1.14)

тобто у два рази менша, ніж в схемі з виводом нульової точки вторинної обмотки трансформатора.

    У мостовій схемі випрямлення струм   і₂ (рис. 1.6, в)  синусоїдний, а не пульсуючий, як у схемі з виводом нульової точки вторинної обмотки трансформатора. 

    Діюче значення струм І₂ знаходять за формулою I₂=U₂/R_d , а з урахуванням (1.2)

                                                          (1.15)

     Струм І₁ зв’язаний зі струмом І₂ співвідношенням

                                                                     (1.16)

       Отже, у однофазній мостовій схемі випрямлення параметри первинної обмотки І₁, U₁ зв’язані з параметрами вторинної обмотки І₂, U₂ коефіцієнтом трансформації n. У відповідності з цим розрахункові потужності обмоток будуть однаковими

                           S₁= S₂= S_т=1,23 Р_d.                                            (1.17)

 

Рис. 1.5. Схема однофазного мостового випрямляча

 

     Із викладеного випливає, що однофазна мостова схема має низку переваг над однофазною з виводом нульової точки вторинної обмотки трансформатора, а саме: для забезпечення заданої потужності у навантаженні потужність трансформатора схеми становить S_т=1,23 Р_d проти S_т=1,48 Р_d ;       

конструкція трансформатора простіша –вторинна обмотка не має виведеної нульової точки; зворотна напруга, на яку слід вибирати діоди схеми, вдвічі менша. Вказані переваги компенсують недолік схеми, який полягає в необхідності мати більшу кількість діодів.

      Режим роботи мостової схеми з активно-індуктивним навантаженням не відрізняється від аналогічного режиму навантаження однофазної схеми з виводом  нульової точки. В цьому випадку струми є змінними, їх форма близька до прямокутної. За умови L_d → ∞ розрахунок діючих значень цих струмів слід вести за такими формулами

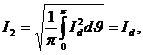                                                 (1.18)

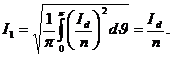                                              (1.19)

      Розрахункові потужності трансформатора та його обмоток у режимі з активно-індуктивним навантаженням будуть меншими, ніж в режимі чисто-активного навантаження і дорівнюють

    S₁=S₂=S_T=1,11P_d.                                          (1.20)

 

Рис. 1.6. Часові діаграми струмів та напруг однофазного мостового випрямляча

       

 

 

Фільтри

    

   Випрямлення змінного струму супроводжується виникненням пульсуючих напруги та струму у навантаженні. Часто пульсації випрямленого струму та напруги негативно впливають на роботу споживача, тому на практиці прагнуть зменшити значення пульсацій і наблизити форму струму до прямої лінії (абсолютно згладженого постійного струму). Зменшення пульсацій випрямленого струму досягають за допомогою пристроїв, які називають фільтрами.

  Криву пульсуючого струму можна розкласти у гармонічний ряд Фур’є і подати як суму постійної (середнє значення струму) і змінних складових. Фільтри застосовуються для зменшення амплітуди змінних складових випрямленого струму у навантаженні. Фільтри складаються із дроселів (котушок індуктивності), конденсаторів та резисторів. Дроселі та конденсатори можуть використовуватися окремо, а також у комбінації, утворюючи Г-, Т-, П-подібні схеми фільтрів.

   Фільтруюча дія дроселів та конденсаторів пов’язана із залежністю їх опору від частоти струму чи напруги. Опір дроселя прямо пропорційний частоті

x_L=2πf_ν L_d,                                          (1.21)

 а опір конденсатора обернено пропорційний частоті

x_c=1/(2π f_ν C_d),                                       (1.22)

де L_d - індуктивність дроселя; С_d - ємність конденсатора; f_ν- частота змінної складової з гармонічного ряду.

    Серед змінних складових (гармонік) випрямленого струму та напруги виділяють основну (у наведених схемах основна гармоніка має подвійну частоту мережі живлення f_ν=1=2f) і за зміною її амплітуди характеризують ефективність роботи фільтра. Відношення амплітуди основної гармоніки випрямленої напруги U_d(1)макс  до постійної складової ( середнього значення) U_d називають коефіцієнтом пульсацій

                                   q₁=U_d(1)макс/U_d.                                           (1.23)

   Принагідно за допомогою формули (1.23) визначимо коефіцієнт пульсацій випрямленої напруги досліджуваних схем випрямлячів. Вище згадувалось, що у випрямленій напрузі  u_d   можна виділити постійну складову (середнє значення) та змінну складову як суму гармонік. Розклад кривої в ряд Фур’є [1] дозволяє визначити амплітуди вищих гармонік

   U_{d(ν)макс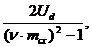}=                                   (1.24)

де ν =1, 2, 3, … - номери  гармонік; m_cx – еквівалентна кількість фаз випрямлення ( для даних схем m_cx = 2).

     Коефіцієнт пульсацій за першою (основною) гармонікою буде дорівнювати                            q₁=                                    (1.25)

      Підставляючи  m_cx = 2 у вираз (1.25) отримаємо, що для досліджуваних схем q₁ = 0,67, тобто амплітуда першої гармоніки становить 67% від U_d.

 

    Відношення коефіцієнтів пульсацій до фільтру q₁ і після q₂ називають коефіцієнтом згладжування фільтра

                                    s = q₁/ q₂=                    (1.26)

де 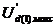- амплітуда основної гармоніки випрямленої напруги на навантаженні (після фільтра).

    Дроселі як елементи фільтра вмикають послідовно з навантаженням, а конденсатори – паралельно до навантаження.

    Ємність C_d  конденсаторного фільтра, увімкненого паралельно навантаженню R_d, залежно від заданого коефіцієнта зглажування s визначають за такою формулою

   C_d = s/(wR_d)=q₁/(q₂wR_d )                                 (1.27)                                                                           

де w – колова частота основної гармоніки випрямленої напруги.

   Індуктивність L_d дроселя фільтра, увімкненого послідовно з резистором R_d, визначають за формулою

      L_d = s R_d /w = q₁ R_d/(q₂w )                             (1.28)                                                                                    

    Широко застосовуються також Г-подібні фільтри, які складаються з дроселя і конденсатора ( конденсатор вмикають паралельно до резистора навантаження R_d ). Коефіцієнт згладжування такого фільтра обчислюється за формулою

                  s=w ²L_dC_d.                                       (1.29)

    Із формули (1.29) можна встановити взаємозалежність параметрів елементів Г-подібного фільтра

L_dC_d=s/w ²=q₁ /(q₂w ²)                            (1.30)

   Вибір параметрів L_d та C_d  Г-подібного фільтра за відомого їх добутку є складною багатофакторною задачею.

   Наведені вище формули приблизні, тому що не враховують активних опорів трансформатора, дроселя та інших елементів схеми випрямляча.

    Послідовне сполучення кількох фільтрів дає змогу отримати еквівалентний коефіцієнт згладжування s, який буде дорівнювати добутку коефіцієнтів згладжування окремих фільтрів

s=s₁×_×s₂×s₃××××s_i .                                             (1.31)

Фільтри впливають на зовнішню характеристику випрямляча.

 

Зовнішня характеристика

 

Зовнішньою характеристикою випрямлячів називають залежність середнього значення випрямленої напруги від середнього значення випрямленого струму U_d=f(I_d).

Аналіз принципу роботи розглянутих схем випрямлячів проведений без врахування активних опорів трансформаторів, провідників, дроселя фільтра та спаду напруги на діодах. Тому такий аналіз є наближеним, оскільки внаслідок спадів напруг на активних опорах елементів від протікання струму реальне середнє значення випрямленої напруги U_d буде меншим від розрахункового (1.2) і буде зменшуватись з ростом струму навантаження I_d. Співвідношення 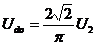 у реальній схемі справедливе для режиму неробочого ходу (I_d=0). Саме тому тут і надалі випрямлена напруга для режиму неробочого ходу позначається індексом «0». Із зростанням струму (I_d>0) на активних опорах схеми будуть зростати спади папруг і середнє значення напруги на навантаженні U_d буде зменшуватись. Зміна напруги U_d відбувається згідно закону 

U_d= U_dо -

де - усереднений за період спад напруги на елементах схеми від проходження струму.

   Зовнішня характеристика випрямляча без фільтра зображена на рис. 1.7

 

Рис. 1.7. Зовнішні характеристики випрямляча (1 – без фільтра; 2, 3 – з ємнісним фільтром С₂>С₁; 4 – з L –C фільтром)

 

 (крива 1). За наявності ємнісного фільтра зовнішня характеристика (крива 2, рис.7) починається з напруги неробочого ходу, яка визначається за формулою  Під час проходження струму I_d в схемі випрямляча виникають втрати напруги, тому зовнішня характеристика нахилена до осі абсцис (осі струму I_d). З ростом струму (внаслідок зменшення опору R_d ) крива 2 зовнішньої характеристики наближається до кривої 1. Це зумовлюється швидшим розряджанням конденсатора фільтра через опір R_d, і пояснюється зменшенням сталої часу 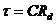. Якщо збільшити ємність конденсатора від С₁ до С₂ , то стала часу  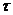збільшиться і зовнішня характеристика буде пологішою (крива 3, рис. 7).

     Зовнішня характеристика випрямляча з L–C фільтром близька до характеристики без фільтра, але має більший нахил внаслідок спаду напруги на активному опорі дроселя фільтра (крива 4, рис.7). Напруга неробочого ходу (коли R_d → ) в схемі з L–C фільтром  Але за умови протікання навіть незначного за значенням струму I_d=I_{d кр} середнє значення випрямленої напруги швидко знижується до U_d 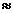 і далі змінюється за залежністю, близькою до характеристик з ємнісним фільтром. На крутій ділянці характеристики (крива 4) за умови I_d<I_{d кр} випрямляч з L–C фільтром працює в режимі переривчастого струму вентилів. Цей режим близький до режиму випрямляча з С- фільтром.

 

Комутація струмів вентилів

 

В розділі 1.6 розглянуто вплив активних опорів елементів схеми на хід

зовнішніх характеристик випрямляча. Реактивні (індуктивні) елементи також впливають на зовнішні характиристики в силу процесів, які відбуваються за їх наявності.

    Реальні електричні кола характеризуються наявністю індуктивностей провідників, трансформаторів, дроселів тощо. Індуктивність є мірою протидії зміні струму в електричному колі. Під час зміни струму в елементах, які характеризуються індуктивністю, наводиться електрорушійна сила (ЕРС) самоіндукції, величина якої пропорційна індуктивності L та швидкості зміни струму di/dt

e_c= - L .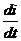

   Напрям e_c протилежний до напряму електрорушійної сили, яка викликає

струм у колі під час зростання струму і збігається з ним під час зменшення струму.

    Наявність індуктивностей L_a в колах протікання струму (рис. 1.8) зумовлює те, що, наприклад, струм i_a2 вентиля VD2  (рис. 1.9) спадає до нуля не в момент часу, коли напруга u_2-2 переходить через нуль від додатних значень до від’ємних, а через деякий час, тобто час протікання струму вентиля збільшується. Явище самоіндукції протидіє також зростанню струму i_a1  вентиля VD1 від нуля до усталеного значення I_d.

 

Рис. 1.8. Контур  струму короткого замикання у однофазному двопівперіодному випрямлячі

 

    Наявність індуктивностей елементів схеми випряляча впливає на процес переходу струму навантаження з одного вентиля на другий – процес комутації струмів вентилів. За відсутності індуктивностей цей процес відбувається миттєво, а за їх наявності тривалість комутації струмів вентилів характеризується кутом γ, який вимірюється в градусах або радіанах. Цей кут називається кутом комутації. Під час комутації обидва вентилі проводять струм, але струм одного з вентилів зростає, а іншого – спадає до нуля.

Відкритий стан одночасно двох вентилів VD1 та VD2 зумовлює протікання струму короткого замикання i_к в контурі, який складається із вторинної обмотки трансформатора, індуктивностей L_a кожної з частин вторинної обмотки трансформатора та вентилів VD1, VD2. Напрям струму визначається напругою u_к= u_2-1 - u_2-2= 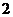(рис. 1.8).

    Кривою струму і_к визначаються закони зміни струмів вентилів VD1, VD2 під час комутації, тривалість якої називають кутом комутації і позначають γ.  Зокрема, струм вентиля VD1, який вступає в роботу, визначається на проміжку γ струмом i_a1= і_к, а струм  вентиля VD2, який виходить з роботи, i_a2=I_d - і_к оскільки у схемі ( див. рис. 1.8) за першим законом Кірхгофа справедливе рівняння струмів i_a1 + i_a2= I_d.     

    Струм і_к в короткозамкнутому контурі обмежується сумарним опором обох частин обмотки трансформатора 2х_а (х_а=2πfL_a) і дорівнює сумi вимушеної та вільної складових

.

     Вимушена складова струму за умови рівності нулю активних опорів в короткозамкнутому контурі r_a=0 відстає відносно напруги на 90º і визначається рівнянням

,

де х_а – індуктивний опір однієї з частин обмотки трансформатора.

 

Рис. 1.9. Часові діаграми струмів та напруг двопівперіодного нульового випрямляча з врахуванням комутаційних процесів (L_d→ ∞; L_а ≠ 0 )

 

  Вільна складова за означеної умови дорівнює сталій інтегрування

.

   Отже, аналітичний вираз струму і_к буде таким

            = .                                (1.32)

    Значення сталої А можна визначити, виходячи з умови, що при J=0 струм і_к=0, тобто 

               .                                   (1.33)

    Отже, струм i_a1 на проміжку γ змінюється за законом

     i_a1= і_к=                                   (1.34)

 і зростає від нуля до значення I_d. Тому, якщо в рівнянні (1.34) підставити J=γ, то отримаємо

                                                      (1.35)

      З цього рівняння можна визначити кут комутації

                                             (1.36)

   Явище комутації струмів вентилів та зумовлене ним протікання струму і_к викликає додатковий спад напруги на індуктивних опорах анодного кола і впливає на хід зовнішньої характеристики випрямляча.

 Визначимо цей додатковий спад напруги.

Провідний стан обох діодів схеми на етапі комутації призведе до того, що потенціал додатного полюса випрямляча φ₊ буде визначатися півсумою вторинних напруг  u_2-1 та u_2-2. Оскільки ці напруги рівні за модулем і зсунуті по фазі між сбою на 180º, то їхня півсума буде дорівнювати нулю. Відповідно випрямлена напруга u_d=φ₊ - φ_- на ділянці комутації буде рівна нулю. Після завершення процесу комутації потенціал додатного полюса буде формувати напруга u_2-2 аж до початку наступної комутації. Середнє значення випрямленої напруги U_d буде меншим від такої ж напруги в режимі без комутації на величину комутаційного спаду напруги U_dγ. Область миттєвих значень  заштрихована на рис. 1.9. Тому напруга U_d може бути записана як

                 U_d= U_dо - U_dγ- U.                                        (1.37)

     Середнє значення комутаційного спаду напруги U_dγ визначається за відомою формулою

U_dγ =

і відповідає площі заштрихованої ділянки. Миттєве значення комутаційного спаду напруги  буде визначатися напругою u_2-1, оскільки миттєве значення випрямленої напруги u_d на проміжку комутації дорівнює нулю. З врахуванням цього

     U_dγ =                             (1.38)

Підставивши в отримане рівняння значення виразу (1-cosγ), визначеного з рівняння (35), отримаємо

   U_dγ =                                            (1.39)

   Результуюче рівняння зовнішньої характеристики однофазного двопівперіодного випрямляча з виводом нульової точки з врахуванням комутаційних процесів буде таким

            U_d=U_dо - U_dγ - U=                   (1.40)

 

1.7.Особливості комутаційних процесів у однофазному мостовому випрямлячі

   Особливість процесів полягає в тому, що на етапі комутації в провідному стані знаходиться одночасно всі чотири діоди (див. контур комутації рис. 1.10).   На схемі показано контур комутації під час вступу в роботу діодів VD1, VD2 і закриванні діодів VD3, VD4. Струм комутації в однофазній мостовій схемі обумовлений напругою u₂  і обмежений індуктивним опором трансформатора x_a та визначається виразом (1.34), тобто як і в однофазній схемі випрямлення з виводом нульової точки трансформатора. Відмінність полягає лише в тому, що в мостовій схемі безпосередньо в комутації кожного з діодів беруть участь складові комутаційного струму і_к1 та і_к2 . За умови рівності цих складових процес комутації завершиться, коли і_к1= і_к2 =I_d. Cтрум і_к= і_к1+ і_к2  в момент завершення комутації   буде рівним 2I_d.

 

Рис. 1.10. Контур комутації в однофазній мостовій схемі

 

Використавши вираз (1.34) та останню умову, отримаємо

    

Звідси різниця 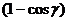 становитиме

 =

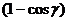Відповідно рівняння зовнішньої характеристики набуде вигляду

                      U_d=U_dо - U_dγ - =                       (1.41)

 тобто комутаційний спад напруги U_dγ в однофазній мостовій схемі вдвічі більший, ніж в однофазній схемі випрямлення з виводом нульової точки трансформатора. Однак вказаний недолік компенсується зменшенням приблизно вдвічі значення індуктивного опору  трансформатора за рахунок кращого магнітного зв’язку вторинної обмотки з первинною і, відповідно, зовнішні характеристики цих двох схем приблизно одинакові.

                                             

 

---

Дата добавления: 2018-02-15; просмотров: 6611; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!