Этап 2. Выбор аппроксимирующей функции
Nbsp; Московский государственный технический университет им. Н.Э. Баумана УТВЕРЖДАЮ Заведующий кафедрой ИУ-6 ________________В.В. Сюзев ___________________2012 г.
Сюзев В. В.
Методические указания
По выполнению курсовой работы по дисциплине
«Системы реального времени»
Москва 2012
Целью данной курсовой работы является приобретение практических навыков проектирования цифровых фильтров (ЦФ). Предметом проектирования выбраны нерекурсивные частотные цифровые фильтры.
Краткие теоретические сведения
Перед выполнением курсовой работы необходимо изучить учебное пособие Сюзева В.В. и Иванова И.П. «Теоретические основы цифровых фильтров», М: МГТУ, 2001. Поэтому приводимые здесь сведения носят справочный характер.
|
|
|
Частотные фильтры.
Частотные фильтры предназначены для целенаправленного изменения частотного состава сигналов. Наиболее распространенными фильтрами являются избирательные фильтры, которые не меняют (пропускают) амплитуду частотных составляющих сигнала в полосе пропускания и подавляют в полосе задержания. Полосы пропускания и задержания ограничены граничными частотами и разделяются обычно полосой частот, в пределах которой амплитуда частотных составляющих сигнала может принимать любые значения. Наличие такой полосы (или нескольких полос, их можно назвать полосами безразличия) позволяет достаточно просто решить проблему борьбы с явлением Гиббса, возникающим при аппроксимации в частотной области разрывных функций.
Основными избирательными фильтрами являются:
1) Фильтры нижних (низких) частот (ФНЧ); 2) фильтры верхних (высоких) частот (ФВЧ); 3) полосовые фильтры (ПФ) и 4) режекторные фильтры (РФ). Амплитудно-частотные характеристики (АЧХ) таких фильтров приведены на рис. 1, 2, 3 и 4 соответственно в функции от нормированной частоты 
где 
круговая частота, а 
интервал дискретизации по времени.
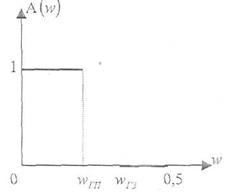
Рис.1 АЧХ ФНЧ
Рис.2 АЧХ ФВЧ
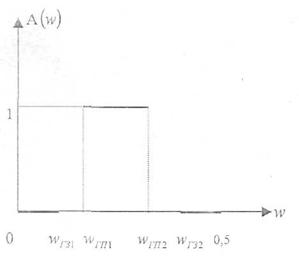
Рис.3 АЧХПФ
Рис.4 АЧХ РФ
|
|
|
Этапы аналитического синтеза цифровых фильтров
Последовательность действий при проектировании ЦФ может быть представлена в виде следующих этапов.
Этап 1. Формирование аппроксимируемой функции
Аппроксимируемые функции B(w) строятся на основе АЧХ А(w) путем доопределения последних в полосах безразличия линейным законом изменения. Такая процедура позволяет из разрывных функций A(w) получить неразрывные функции В(w) и устранить погрешности аппроксимации, возникающие из-за явления Гиббса.
Для ранее перечисленных избирательных ЦФ аппроксимируемые функции приобретают следующий вид:
ФНЧ
ФВЧ
ПФ
РФ
Этап 2. Выбор аппроксимирующей функции
Аппроксимирующая функция 
должна достаточно просто зависеть от импульсной характеристики (ИХ) ЦФ 
или связанных с ней коэффициентов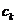 
. Обычно для этих целей используются линейные зависимости от 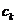. Вид этих зависимостей зависит от вида фильтра, который в свою очередь зависит от свойств симметрии и антисимметрии ИХ и четности или нечетности памяти фильтра N. В соответствии с этим возможны четыре вида ЦФ:
вид 1: N - нечетное, ИХ - симметричная;
вид 2: N - четное, ИХ - симметричная;
вид 3: N - нечетное, ИХ - антисимметричная;
|
|
|
вид 4: N - четное, ИХ - симметричная.
Области возможного применения данных видов ЦФ при реализации избирательных фильтров указаны в таблице.
Таблица
| Избиратель-ный фильтр | Вид фильтра | |||
| 1 | 2 | 3 | 4 | |
| ФНЧ | + | + | - | - |
| ФВЧ | + | - | - | + |
| ПФ | + | + | + | + |
| РФ | + | - | - | - |
Аппроксимирующие функции для конкретных видов фильтров имеют следующий вид:
Вид 1:
Вид 2:
Вид 3:
Вид 4:
Дата добавления: 2018-02-15; просмотров: 778; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!