Статистические методы изучения связей социально – экономических явлений
Задача № 50.
Имеются следующие данные по торговым предприятиям фирм, тыс. руб.
| Товарооборот | Издержки обращения |
| 6700 | 350 |
| 5600 | 270 |
| 6300 | 400 |
| 6100 | 360 |
| 6500 | 310 |
| 5200 | 280 |
| 5000 | 300 |
| 5500 | 240 |
| 4700 | 700 |
| 5800 | 320 |
Для установления связи между издержками обращения и товарооборотом рассчитайте ранговый коэффициент Спирмена.
Задача № 51.
По ряду районов края определены: среднесуточное количество йода в воде и пище и пораженности населения заболеванием щитовидной железы.
| Номер района | Количество йода в воде и пище, усл. ед. | Пораженность населения заболеванием щитовидной железы, % |
| 1 | 2 | 3 |
| 1 | 201 | 0,2 |
| 2 | 178 | 0,6 |
| 3 | 155 | 1,1 |
| 4 | 154 | 0,8 |
| 5 | 126 | 2,5 |
| 1 | 2 | 3 |
| 6 | 81 | 4,4 |
| 7 | 71 | 16,9 |
Для оценки тесноты связи пораженности заболеванием щитовидной железы с количеством йода в воде и пище определите коэффициенты корреляции рангов Спирмена, Кендалла и Фехнера.
Задача № 52.
При проверке качества товара, поступившего в магазин, получены следующие данные, в %%:
| Категории качества товара | Удельный вес стандартной продукции | Удельный вес нестандартной продукции | Итого |
| Высшая | 90 | 10 | 100 |
| Первая | 70 | 30 | 100 |
Установитетесноту связи между качеством товара и удельным весом стандартной и нестандартной продукции с помощью коэффициентов взаимной сопряженности Пирсона и Чупрова.
|
|
|
Задача № 53.
Используя коэффициент взаимной сопряженности Пирсона ответьте на вопрос: являются ли конфликтные ситуации фактором гипертонической болезни?
| Конфликтные ситуации на работе | Обследовано на заводе, чел. | ||
| Всего | Больные гипертонией | Здоровые | |
| Есть | 35 | 28 | 7 |
| Нет | 55 | 17 | 38 |
| Итого | 90 | 45 | 45 |
Задача № 54.
С помощью коэффициента взаимной сопряженности Пирсона определите:является ли работа на компьютере фактором ухудшения зрения,
чел.
| Работа за компьютером | Состояние зрения за 3 года | Всего | |
| Не ухудшилось | Ухудшилось | ||
| Не работает | 70 | 5 | 75 |
| Недавно работает | 60 | 20 | 80 |
| Давно работает | 10 | 45 | 55 |
| Итого | 140 | 70 | 210 |
Задача № 55.
По материалам одного из обследований домашних хозяйств получены следующие данные:
| Доход | В составе совокупных доходов семьи | Всего | |
| есть доход от предпринимательской деятельности | нет дохода от предпринимательской деятельности | ||
| Выше прожиточного минимума | 140 | 120 | 260 |
| Ниже прожиточного минимума | 90 | 340 | 430 |
| Итого | 230 | 460 | 690 |
Найдитекоэффициент ассоциации между источниками доходов (наличием дохода от предпринимательской деятельности) и уровнем дохода.
|
|
|
Задача № 56.
В результате обследования населения региона получены следующие данные:
| Семейное положение | Число семей | Всего | |
| имеющих садовый участок | не имеющих садовый участок | ||
| Неполные семьи | 120 | 80 | 200 |
| Полные семьи | 600 | 200 | 800 |
| Итого | 720 | 280 | 1000 |
Установите тесноту связи между семейным положением и наличием садового участка, рассчитав коэффициент контингенции.
Задача № 57.
Зависимость между объемом реализации и валовой прибылью по предприятиям одной из отраслей характеризуется следующими данными:
| № предприятия | Выручка от реализации, млн. руб. | Валовая прибыль, тыс. руб. |
| 1 | 17 | 500 |
| 2 | 22 | 750 |
| 3 | 86 | 910 |
| 4 | 13 | 820 |
| 5 | 47 | 1000 |
| 6 | 58 | 700 |
| 7 | 34 | 80 |
| 8 | 84 | 1250 |
| 9 | 91 | 1060 |
| 10 | 106 | 1520 |
| 11 | 125 | 1100 |
| 12 | 108 | 1280 |
| 13 | 183 | 1660 |
| 14 | 110 | 1600 |
Для изучения влияния объема реализации на величину валовой прибыли постройте уравнение прямой, рассчитайте параметры уравнения и определитетесноту связи с помощью линейного коэффициента корреляции.
Сделайте выводы.
Задача № 58.
По 16 предприятиям, изготавливающим одноименные запасные детали к сельскохозяйственным машинам, были получены следующие данные об объеме производства деталей и долей ручных работ:
|
|
|
| № пред- приятия | Объем производства, тыс. шт. | Доля ручных работ, % | № пред- приятия | Объем производства, тыс. шт. | Доля ручных работ, % |
| 1 | 12 | 12 | 9 | 45 | 4 |
| 2 | 18 | 10 | 10 | 50 | 4 |
| 3 | 20 | 14 | 11 | 60 | 3 |
| 4 | 25 | 8 | 12 | 70 | 3 |
| 5 | 30 | 6 | 13 | 82 | 2 |
| 6 | 32 | 7 | 14 | 91 | 2 |
| 7 | 35 | 5 | 15 | 99 | 1 |
| 8 | 40 | 5 | 16 | 120 | 1 |
Определите вид корреляционной зависимости, постройте уравнение регрессии, рассчитайте параметры уравнения, коэффициент эластичности между фактором и результатом, вычислите показатель тесноты связи, дайте анализ полученных данных.
Задача № 59.
Имеются данные о стоимости основных фондов и среднесуточной переработке сырья по 22 предприятиям:
| №№ п\п | Стоимость основных фондов, млн. руб. | Среднесуточная переработка сырья, тыс. ц. |
| 1 | 25 | 4,5 |
| 2 | 35 | 6,0 |
| 3 | 35 | 7,8 |
| 4 | 39 | 4,2 |
| 5 | 43 | 5,0 |
| 6 | 42 | 5,8 |
| 7 | 45 | 5,1 |
| 8 | 50 | 6,2 |
| 9 | 54 | 7,0 |
| 10 | 45 | 8,0 |
| 11 | 50 | 9,0 |
| 12 | 54 | 8,5 |
| 13 | 55 | 6,3 |
| 14 | 60 | 8,0 |
| 15 | 62 | 10,0 |
| 16 | 63 | 11,4 |
| 17 | 60 | 10,0 |
| 18 | 70 | 11,0 |
| 19 | 74 | 11,8 |
| 20 | 72 | 11,2 |
| 21 | 76 | 12,0 |
| 22 | 79 | 11,6 |
Для изучения тесноты связи между среднесуточной переработкой сырья и стоимостью основных фондов вычислитекоэффициент детерминации и эмпирическое корреляционное отношение, сгруппировав данные по стоимости основных фондов с равным интервалом. Поясните результаты.
|
|
|
Решение типовых задач.
Задача № 1.
Экспертами оценивались вкусовые качества вин Суммарные оценки получены следующие:
| Марка вина | Оценка в баллах | Цена в условных единицах |
| 1 | 11 | 1,57 |
| 2 | 12 | 1,60 |
| 3 | 17 | 2,00 |
| 4 | 15 | 2,10 |
| 5 | 13 | 1,70 |
| 6 | 14 | 1,85 |
| 7 | 18 | 1,80 |
| 8 | 10 | 1,15 |
| 9 | 19 | 2,30 |
| 10 | 25 | 2,40 |
Согласуется ли оценка вина с его ценой? Проверим эту гипотезу методом ранговой корреляции Спирмена и коэффициентом Фехнера.
Решение:
Оценку тесноты связи с помощью коэффициента Спирмена и Фехнера рассчитываем в табличной форме
| Марка вина | Цена (х) | Оценка (у) | Квадрат разности рангов d²=(Rx-Ry)² | Знак отклонения от средней арифметич. | |||
| Усл. ед. | РангRx | Баллы | РангRy | 
| 
| ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1,57 | 2 | 11 | 2 | 6 | - | - |
| 2 | 1,60 | 3 | 14 | 5 | 4 | - | - |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 2,00 | 7 | 17 | 7 | 0 | + | + |
| 4 | 2,10 | 8 | 16 | 6 | 4 | + | +- |
| 5 | 1,70 | 4 | 12 | 3 | 1 | - | - |
| 6 | 1,85 | 6 | 13 | 4 | 9 | + | - |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7 | 1,80 | 5 | 18 | 8 | 9 | - | + |
| 8 | 1,15 | 1 | 10 | 1 | 0 | - | - |
| 9 | 2,30 | 9 | 19 | 9 | 0 | + | + |
| 10 | 2,40 | 10 | 25 | 10 | 0 | + | + |
| Итого | 18,17 | х | 155 | х | 27 | х | Х |
Коэффициент Спирмена: 





 Следовательно, связь прямая и тесная.
Следовательно, связь прямая и тесная.
Проверяем значимость полученных результатов по t-критерию Стьюдента  . При уровне значимости 0,05 tТ= 2,262. Следовательно, значимость результатов подтверждается т.к.
. При уровне значимости 0,05 tТ= 2,262. Следовательно, значимость результатов подтверждается т.к. 
Для определения коэффициента Фехнера рассчитаем среднее значение цены
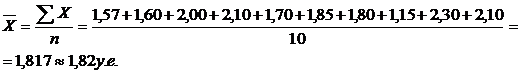
и среднее значение оценки
 Тогда количество совпадений знаков отклонений
Тогда количество совпадений знаков отклонений 
будет восемь, а несовпадений два. Отсюда коэффициент Фехнера
Кф= 

Следовательно, связь прямая и существенная.
Задача № 2.
На основании следующих условных данных необходимо исследовать связь между успеваемостью студентов – заочников одного из вузов и их работой по специальности с помощью коэффициентов ассоциации и контингенции.
| Студенты-заочники | Число студентов | в том числе | |
| получивших положительные оценки | получивших неудовлетворительные оценки | ||
| Работающие по специальности | 200 а+с | 180 а | 20 с |
| Работающие не по специальности | 200 b+d | 140 b | 60 d |
| Итого | 400 a+c+b+d | 320 a+b | 80 c+d |
Коэффициент ассоциации

Связь подтверждается т.к. Ка > 0,5
Коэффициент контингенции
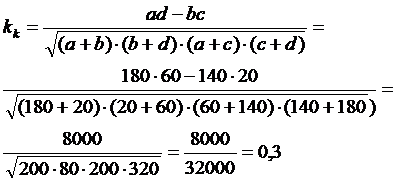
Связь подтверждается т.к. Кк=0,3
Задача № 3.
С помощью коэффициентов взаимной сопряженности Пирсона и Чупрова необходимо исследовать связь между себестоимостью продукции и производительностью труда на основании нижеследующих данных:
| Себестоимость | Производительность труда | Итого | ||
| Высокая | Средняя | Низкая | ||
| Низкая | 19 | 12 | 9 | 40 |
| Средняя | 7 | 18 | 15 | 40 |
| Высокая | 4 | 10 | 26 | 40 |
| Итого | 30 | 40 | 50 | 120 |
Коэффициент Пирсона

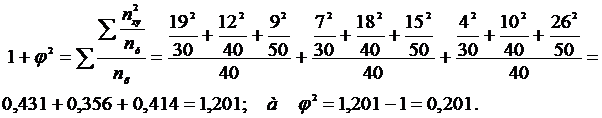
Следовательно, связь подтверждается, т.к. КП >0,3
Коэффициент Чупрова

Следовательно связь подтверждается, т.к. КЧ=0,3
Задача № 4.
По результатам экспертной оценки степени влияния факторов на уровень производительности труда факторам были присвоены следующие ранги:
| Фактор | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Ранг экспертов (х) | 7 | 4 | 1 | 3 | 14 | 13 | 10 | 12 | 5 | 9 | 8 | 2 | 11 | 15 | 6 |
| Ранг после расчета коэффициента корреляции (у) | 4 | 6 | 3 | 7 | 15 | 11 | 14 | 12 | 1 | 13 | 5 | 2 | 9 | 10 | 8 |
Определить с помощью коэффициента корреляции рангов Кендалла насколько точно результаты экспертной оценки предугадали действительную степень влияния факторов на уровень производительности труда.
Решение:
Расположим ранги в порядке возростания факторного признака
(ранг экспертов)
| Ранг экспертов (х) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Ранг после расчета коэффициента корреляции (у) | 3 | 2 | 7 | 6 | 1 | 8 | 4 | 5 | 13 | 14 | 9 | 12 | 11 | 15 | 10 |
Первому значению у=3 соответствует 12 чисел (7,6,8,4,5,13,14,9,12,11,15,10),которые расположены после 3 и больше 3; второму значению у=2 соответствует тоже 12 чисел (7,6,8,4,5,13,14,9,12,11,15,10),которые расположены после 2 и больше 2; третьему значению у=7 соответствует 8 чисел (8,13,14,9,12,11,15,10), которые больше 7; четвертому значению у=6 соответствует тоже 8 значений(8,13,14,9,12,11,15,10), которые больше 6 и так далее: больше 1 десять значений; больше 8 семь значений; больше 4 восемь значений; больше 5 семь значений; больше13 два значения; больше14 одно значение; больше 9 четыре значения; больше12 одно значение; больше 11 тоже одно значение; больше 15 нет ни одного значения. Отсюда Р=12+12+8+8+10+7+8+7+2+1+4+1+1+0=81.
Далее определяем Q =24,т.е. количество чисел после каждого из членов последовательности рангов переменной у, имеющих ранг меньше, чем у рассматриваемого. Эти числа берутся со знаком минус. Так после у=3 два числа (-2,-1) меньше 3; для у=2 одно число (-1) меньше 2, для у=7 четыре числа (-6,-1,-4,-5) и так далее. Отсюда Q=-2-1-4-3-0-2-0-0-4-4-0-2-1-1= -24.
Следовательно степень влияния отобранных факторов на производительность труда экспертами была существенной, т. к. коэффициент корреляции рангов Кэндалла:

Проверяем значимость коэффициента Кендала по t критерию Стьюдента
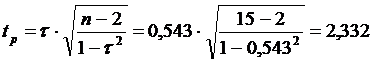 При уровне значимости 0,05 tт =2,145 Следовательно, значимость подтверждается т.к.
При уровне значимости 0,05 tт =2,145 Следовательно, значимость подтверждается т.к. 
Задача № 5.
По данным о стоимости основных фондов и объеме произведенной продукции определите уравнение связи и тесноту связи:
| Стоимость основных фондов, млн. руб.(х) | Объем произведенной продукции, млн. руб. (у) | xy | x² | y² | 
|
| А | Б | 1 | 2 | 3 | 4 |
| 1 | 20 | 20 | 1 | 400 | 19,4 |
| 2 | 25 | 50 | 4 | 625 | 25,0 |
| 3 | 31 | 93 | 9 | 961 | 30,6 |
| А | Б | 1 | 2 | 3 | 4 |
| 4 | 31 | 124 | 16 | 961 | 36,2 |
| 5 | 40 | 200 | 25 | 1600 | 41,8 |
| 6 | 56 | 330 | 36 | 3136 | 47,4 |
| 7 | 52 | 364 | 49 | 2704 | 53,0 |
| 8 | 60 | 480 | 64 | 3600 | 58,6 |
| 9 | 60 | 540 | 81 | 3600 | 64,2 |
| 10 | 70 | 700 | 100 | 4900 | 69,8 |
| 55 | 445 | 2907 | 385 | 22487 | 446,0 |
Связь предполагается линейная, уравнение прямой 
Решаем систему уравнений методом наименьших квадратов



Коэффициент регрессии а1 свидетельствует о том, что при увеличении объема основных фондов на 1млн. руб. количество произведенной продукции увеличится на 5,6 млн. руб.

Тесноту связи определяем по линейному коэффициенту корреляции
Следовательно, связь прямая и очень тесная.
Задача № 6.
По сельхозпредприятиям имеются данные об урожайности и количестве внесенных минеральных удобрений. Выявить зависимость урожайности от количества внесенных минеральных удобрений.
| № № с/х предприятия | Внесено удобрений на 1 га, ц (х) | Урожайность ц\га (у) | х² | х³ | х4 | ху | х²у | 
| 
|
| 1 | 0,4 | 14 | 0,16 | 0,064 | 0,0256 | 5,8 | 2,24 | 14,98 | 196 |
| 2 | 0,5 | 16 | 0,25 | 0,125 | 0,0625 | 8,0 | 4,00 | 17,11 | 256 |
| 3 | 0,5 | 19 | 0,25 | 0,125 | 0,0625 | 9,5 | 4,75 | 17,11 | 361 |
| … | … | … | … | … | … | … | … | … | … |
| 29 | 1,4 | 32 | 1,96 | 2,744 | 3,8416 | 44,8 | 62,72 | 30,02 | 1024 |
| 30 | 1,5 | 30 | 2,25 | 3,375 | 5,0625 | 45,0 | 67,50 | 30,77 | 900 |
| Итого | 30,0 | 750 | 32,9 | 38,484 | 47,0762 | 791,1 | 899,95 | 750,0 | 20400 |
Произведем выравнивание по параболе второго порядка: 
Решаем систему нормальных уравнений:


Решение этой системы уравнений методом наименьших квадратов дает следующие значения параметров:
ао=5‚086 а1=27‚511 а2= -6‚927
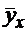 =5‚086+27‚511x-6‚927x²
=5‚086+27‚511x-6‚927x²
Т.к. связь криволинейная для определения тесноты связи используется корреляционное отношение:
 , где общая дисперсия признака
, где общая дисперсия признака  ,
,  ¸ а межгрупповая дисперсия
¸ а межгрупповая дисперсия 
Общая дисперсия определятся по исходным (не сгруппированным) данным, т.е. 
Для нахождения межгрупповой дисперсии необходимо произвести группировку предприятий по количеству внесенных минеральных удобрений.
Результат группировки данных по стоимости основных фондов представлен в нижеследующей таблице
| Группы с/х предприятий по количеству внесенных минеральных удобрений на 1 га, ц. | Количество предприятий | Средняя урожайность, ц/га |
| 0,3 – 0,5 | 4 | 14 |
| 0,5 – 0,7 | 5 | 16 |
| 0,7 – 0,9 | 9 | 32 |
| 0,9 – 1,1 | 6 | 29 |
| 1,1 - 1,3 | 4 | 28 |
| 1,3 и более | 2 | 20 |
В данной задаче факторный признак количество минеральных удобрений (х),
а результативный – урожайность (у). Межгрупповая дисперсия  ;
;
 вычисляем по данным группировки в вышеизложенной таблице
вычисляем по данным группировки в вышеизложенной таблице  – средняя урожайность в каждой группе, т.е.
– средняя урожайность в каждой группе, т.е.

Общая средняя признака  ,
,  -число предприятий в каждой группе,
-число предприятий в каждой группе,  = 30 заводам.
= 30 заводам.
Составим расчетную таблицу:

| 
| (  ) )
| 
| 
|
| 14 | 4 | -11 | 121 | 484 |
| 16 | 5 | -9 | 81 | 405 |
| 32 | 9 | 7 | 49 | 441 |
| 29 | 6 | 4 | 16 | 96 |
| 28 | 4 | 3 | 9 | 36 |
| 20 | 2 | -5 | 25 | 50 |
| Итого | 30 | х | х | 1512 |
Определяем межгрупповую дисперсию  =1512/30=50,4. Теперь можно вычислить корреляционное отношение:
=1512/30=50,4. Теперь можно вычислить корреляционное отношение:  =
=  . Это означает, что связь между количеством внесенных минеральных удобрений и урожайностью тесная.
. Это означает, что связь между количеством внесенных минеральных удобрений и урожайностью тесная.
Дата добавления: 2018-02-15; просмотров: 797; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
